山东省枣庄市峄城区2018-2019学年八年级下学期数学3月月考试卷
试卷更新日期:2020-04-02 类型:月考试卷
一、选择题(12×3)
-
1. 若a<b,则下列结论不一定成立的是( )A、a﹣1<b﹣1 B、2a<2b C、﹣ >﹣ D、a2<b22. 下列命题的逆命题是真命题的是( )A、如果a>0,b>0,则a+b>0 B、直角都相等 C、两直线平行,同位角相等 D、若a=b,则|a|=|b|3. 不等式x+1≥2x﹣1的解集在数轴上表示为( )A、
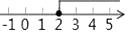 B、
B、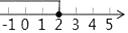 C、
C、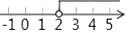 D、
D、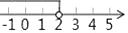 4. 到三角形三条边的距离都相等的点是这个三角形的( )A、三条中线的交点 B、三条高的交点 C、三条边的垂直平分线的交点 D、三条角平分线的交点5. 不等式组 的正整数解的个数是( )
4. 到三角形三条边的距离都相等的点是这个三角形的( )A、三条中线的交点 B、三条高的交点 C、三条边的垂直平分线的交点 D、三条角平分线的交点5. 不等式组 的正整数解的个数是( )
A、5 B、4 C、3 D、26. 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于 MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=4,AB=15,则△ABD的面积是( ) A、15 B、30 C、45 D、607. 一次函数y=﹣3x+b和y=kx+1的图象如图所示,其交点为P(3,4),则不等式kx+1≥﹣3x+b的解集在数轴上表示正确的是( )
A、15 B、30 C、45 D、607. 一次函数y=﹣3x+b和y=kx+1的图象如图所示,其交点为P(3,4),则不等式kx+1≥﹣3x+b的解集在数轴上表示正确的是( ) A、
A、 B、
B、 C、
C、 D、
D、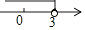 8. 如图,在△ABC中,分别以点A和点C为圆心,大于 AC长为半径画弧,两弧相交于点M,N,作直线MN分别交BC,AC于点D,E.若AE=3cm,△ABD的周长为13cm,则△ABC的周长为( )
8. 如图,在△ABC中,分别以点A和点C为圆心,大于 AC长为半径画弧,两弧相交于点M,N,作直线MN分别交BC,AC于点D,E.若AE=3cm,△ABD的周长为13cm,则△ABC的周长为( )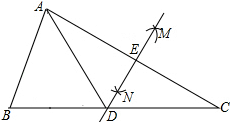 A、16cm B、19cm C、22cm D、25cm9. 已知关于x的不等式组 仅有三个整数解,则a的取值范围是( )
A、16cm B、19cm C、22cm D、25cm9. 已知关于x的不等式组 仅有三个整数解,则a的取值范围是( )
A、 ≤a<1 B、 ≤a≤1 C、 <a≤1 D、a<110. 如图,折叠直角三角形纸片,使点C落在AB上的点E处.已知BC=12,∠B=30°,∠C=90°,则DE的长是( )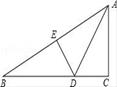 A、6 B、4 C、3 D、211. 某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到吴江儿童福利院看望孤儿.如果分给每位儿童4盒牛奶,那么剩下28盒牛奶;如果分给每位儿童5盒牛奶,那么最后一位儿童分不到5盒,但至少能有2盒.则这个儿童福利院的儿童最少有( )A、28人 B、29人 C、30人 D、31人12. 如图,点E在△DBC的边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论:
A、6 B、4 C、3 D、211. 某校学生志愿服务小组在“学雷锋”活动中购买了一批牛奶到吴江儿童福利院看望孤儿.如果分给每位儿童4盒牛奶,那么剩下28盒牛奶;如果分给每位儿童5盒牛奶,那么最后一位儿童分不到5盒,但至少能有2盒.则这个儿童福利院的儿童最少有( )A、28人 B、29人 C、30人 D、31人12. 如图,点E在△DBC的边DB上,点A在△DBC内部,∠DAE=∠BAC=90°,AD=AE,AB=AC.给出下列结论:①BD=CE;②∠ABD+∠ECB=45°;③BD⊥CE;④BE2=2(AD2+AB2)﹣CD2 . 其中正确的是( )
 A、①②③④ B、②④ C、①②③ D、①③④13. 用反证法证明命题“三角形中必有一个内角小于或等于60°”时,首先应假设这个三角形中14. 已知点O为△ABC三边垂直平分线的交点,点O到顶点A的距离为6cm,则OA+OB+OC=.15. 如图,△ABC中,AB=AC,DE是AB的垂直平分线,AB=8,BC=4,∠A=36°,则∠DBC= ,△BDC的周长是 .
A、①②③④ B、②④ C、①②③ D、①③④13. 用反证法证明命题“三角形中必有一个内角小于或等于60°”时,首先应假设这个三角形中14. 已知点O为△ABC三边垂直平分线的交点,点O到顶点A的距离为6cm,则OA+OB+OC=.15. 如图,△ABC中,AB=AC,DE是AB的垂直平分线,AB=8,BC=4,∠A=36°,则∠DBC= ,△BDC的周长是 . 16. 已知关于x的不等式组 无解,则a的取值范围是 .17. 在△ABC中,AB=2 ,BC=1,∠ABC=45°,以AB为一边作等腰直角三角形ABD,使∠ABD=90°,连接CD,则线段CD的长为 .18. 如图,在平面直角坐标系中,点A1 , A2 , A3 , …和B1 , B2 , B3 , …分别在直线y= x+b和x轴上.△OA1B1 , △B1A2B2 , △B2A3B3 , …都是等腰直角三角形.如果点A1(1,1),那么点A2019的纵坐标是 .
16. 已知关于x的不等式组 无解,则a的取值范围是 .17. 在△ABC中,AB=2 ,BC=1,∠ABC=45°,以AB为一边作等腰直角三角形ABD,使∠ABD=90°,连接CD,则线段CD的长为 .18. 如图,在平面直角坐标系中,点A1 , A2 , A3 , …和B1 , B2 , B3 , …分别在直线y= x+b和x轴上.△OA1B1 , △B1A2B2 , △B2A3B3 , …都是等腰直角三角形.如果点A1(1,1),那么点A2019的纵坐标是 .
二、解答题
-
19. 解下列不等式 ,并把解集在数轴表示出来.20. 已知:如图,∠ABC,射线BC上一点D.

求作:等腰△PBD,使线段BD为等腰△PBD的底边,点P在∠ABC内部,且点P到∠ABC两边的距离相等.
21. 解不等式组,并将解集在数轴上表示出来.22. 如图,∠A=∠D=90°,AC=DB,AC、DB相交于点O.求证:OB=OC.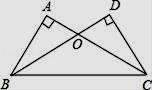 23. 友谊商店A型号笔记本电脑的售价是a元/台,最近,该商店对A型号笔记本电脑举行促销活动,有两种优惠方案,方案一:每台按售价的九折销售,方案二:若购买不超过5台,每台按售价销售,若超过5台,超过的部分每台按售价的八折销售,某公司一次性从友谊商店购买A型号笔记本电脑x台。(1)、当x=8时,应选择哪种方案,该公司购买费用最少?最少费用是多少元?(2)、若该公司采用方案二方案更合算,求x的范围。24. 已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点.
23. 友谊商店A型号笔记本电脑的售价是a元/台,最近,该商店对A型号笔记本电脑举行促销活动,有两种优惠方案,方案一:每台按售价的九折销售,方案二:若购买不超过5台,每台按售价销售,若超过5台,超过的部分每台按售价的八折销售,某公司一次性从友谊商店购买A型号笔记本电脑x台。(1)、当x=8时,应选择哪种方案,该公司购买费用最少?最少费用是多少元?(2)、若该公司采用方案二方案更合算,求x的范围。24. 已知,在△ABC中,∠A=90°,AB=AC,点D为BC的中点. (1)、如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;(2)、若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.25. 在△ABC中,AB=AC , 点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE , 使AD=AE , ∠DAE=∠BAC , 连接CE .
(1)、如图①,若点E、F分别为AB、AC上的点,且DE⊥DF,求证:BE=AF;(2)、若点E、F分别为AB、CA延长线上的点,且DE⊥DF,那么BE=AF吗?请利用图②说明理由.25. 在△ABC中,AB=AC , 点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE , 使AD=AE , ∠DAE=∠BAC , 连接CE .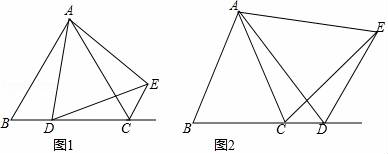 (1)、如图①,若△ABC是等边三角形,且AB=AC=2,点D在线段BC上.
(1)、如图①,若△ABC是等边三角形,且AB=AC=2,点D在线段BC上.①求证:∠BCE+∠BAC=180°;
②当四边形ADCE的周长取最小值时,求BD的长.
(2)、若∠BAC≠60°,当点D在射线BC上移动,如图②,则∠BCE和∠BAC之间有怎样的数量关系?并说明理由.