山西省临汾市2019-2020学年八年级数学第五次月考试卷

试卷更新日期：2020-04-01 类型：月考试卷

进入出卷网下载

一、选择题(本大题共10个小题，每小题3分，共30分。)

1. 如图，在数轴上所表示的x的取值范围中，有意义的二次根式是（）

A、 $\sqrt{x - 3}$ B、 $\sqrt{x + 3}$ C、 $\frac{1}{\sqrt{x - 3}}$ D、 $\frac{1}{\sqrt{x + 3}}$

查看试题解析
2. 下列二次根式中，属于最简二次根式的是（）

A、 $\sqrt{0.5}$ B、 $\sqrt{\frac{1}{5}}$ C、 $\sqrt{50}$ D、 $\sqrt{5}$

查看试题解析
3. 计算 $\sqrt{45} + \sqrt{20}$ 的结果是（）

A、65 B、 $\sqrt{65}$ C、5 $\sqrt{5}$ D、5 $\sqrt{10}$

查看试题解析
4. 下列各组数中，是勾股数的是（）

A、0.3，0.4，0.5 B、 $\sqrt{5}$ ， $\sqrt{12}$ ， $\sqrt{13}$ C、6，8，10 D、1.5，2，2.5

查看试题解析
5. 如图所示的是由两个直角三角形和三个正方形组成的图形，其中阴影部分的面积是（）

A、50 B、16 C、25 D、41

查看试题解析
6. 如图，在直角三角形ABC中，∠B=90°，AB=CB，则以下式子一定成立的是（）

A、a²+b²=c² B、(a+c)²=b² C、(a+b)(a-b)=c² D、b²=2a²

查看试题解析
7. 如图，在平面直角坐标系中，点P的坐标为(-2，3)，以点O为圆心，OP的长为半径画弧，交x轴的负半轴于点A，则点A的横坐标为（）

A、 $\sqrt{13}$ B、 $2 - \sqrt{13}$ C、 $- \sqrt{13}$ D、 $- \sqrt{13} - 2$

查看试题解析
8. 在数学课上，老师将一长方形纸片的长增加2 $\sqrt{3}$ cm，宽增加7 $\sqrt{3}$ cm，就成为了一个面积为192cm²的正方形，则原长方形纸片的面积为（）

A、18cm² B、20cm² C、36cm² D、48cm²

查看试题解析
9. 勾股定理是人类最伟大的科学发现之一，在我国古代算书《周髀算经》中早有记载．如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大的正方形内．若知道图中阴影部分的面积，则一定能求出（）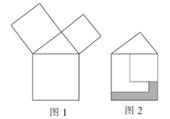

A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和

查看试题解析
10. 如图，在Rt△ABC中，∠ACB=90°，AB=5cm，AC=3cm，动点P从点B出发，沿射线BC以1cm/s的速度移动，设运动的时间为t秒，当△ABP为等腰三角形时，t的值不可能为（）

A、5 B、8 C、 $\frac{25}{4}$ D、 $\frac{25}{8}$

查看试题解析

二、填空题(本大题共5个小题，每小题3分，共15分)

11. $\sqrt{2} \cdot \sqrt{5}$ 的计算结果是。

查看试题解析
12. 若两个最简二次根式 $\sqrt{5}$ 与 $\sqrt{2 m - 5}$ 能够合并，则m=。

查看试题解析
13. 在△ABC中，∠C=90°，若AB= $\sqrt{5}$ ，则AB²+AC²+BC²=。

查看试题解析
14. 已知三角形的三边长分别为 $\sqrt{6}$ ， $\sqrt{6}$ ， $2 \sqrt{3}$ ，则此三角形的最长边上的高等于。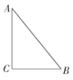

查看试题解析
15. 我们定义新运算：a⊕b= $\frac{\sqrt{a b}}{b}$ ，例如：3⊕2= $\frac{\sqrt{3 \times 2}}{2} = \frac{\sqrt{6}}{2}$ ，那么（12⊕3）⊕6的值为。

查看试题解析

三、解答题(本大题共8个小题，共75分．)

16.

(1)、计算：
$\frac{\sqrt{10} - \sqrt{15}}{\sqrt{5}} \times \sqrt{3}$

(2)、在Rt△ABC中，∠C=90°，∠A、∠B、∠C的对边分别为a、b、c．若a：c=15：17，b=24，求a的值。

查看试题解析
17. 计算：
$(2 \sqrt{5} + 5 \sqrt{2}) (2 \sqrt{5} - 5 \sqrt{2}) - {(\sqrt{5} + \sqrt{2})}^{2}$

查看试题解析
18. 我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”，即已知三角形的三边长，求它的面积。用符号表示为S= $\sqrt{\frac{1}{4} [(a^{2} b^{2} - {(\frac{a^{2} + b^{2} - c^{2}}{2})}^{2}]}$ (其中a，b，c为三角形的三边长，S为三角形的面积)．请利用这个公式求出当a= $\sqrt{5}$ ，b=3，c=2 $\sqrt{5}$ 时的三角形的面积。

查看试题解析
19. 如图，在平面直角坐标系中，点A的坐标为( $\sqrt{2}$ ，0)，点A关于y轴的对称点为B。以AB为一边向上作一个等边△ABC。

(1)、求点C的坐标。

(2)、求△ABC的周长和面积。

查看试题解析
20. 如图1，一架云梯斜靠在一竖直的墙上，云梯的顶端距地面15米，云梯的长度比云梯底端离墙的距离长5米。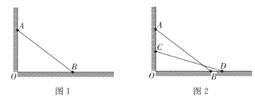

(1)、这个云梯的底端离墙多远？

(2)、如图2，如果云梯的顶端下滑了8m，那么云梯的底部在水平方向滑动了多少米？

查看试题解析
21. 【阅读理解】小明在学习二次根式后，发现一些含根号的式子可以写成另一个式子的平方，如：3+2 $\sqrt{2}$ =(1+ $\sqrt{2}$ )² ，善于思考的小明进行了以下探索：
设a+ $\sqrt{2}$ b=(m+ $\sqrt{2}$ n)²(其中a、b、m、n均为整数)，则有a+ $\sqrt{2}$ b=m²+2n²+2 $\sqrt{2}$ mn，∴a=m²+2n²，b=2mn，这样小明就找到了一种把类似a+ $\sqrt{2}$ b的式子化为平方式的方法。

(1)、【学习体会】
当a、b、m、n均为正整数时，若a+ $\sqrt{3}$ b=(m+n $\sqrt{3}$ )² ，用含m、n的式子分别表示a、b；a= ， b=。

(2)、利用探索后得到的结论，用完全平方式表示：7+4 $\sqrt{3}$ =。

(3)、【灵活运用】
请化简： $\sqrt{12 - 6 \sqrt{3}}$ 。

查看试题解析
22. 如图，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，AB=AC，AD=AE。

(1)、求证：△ACE≌△ABD。

(2)、若AC=2，EC=4，DC=2 $\sqrt{2}$ ，求∠ACD的度数。

(3)、在(2)的条件下，直接写出DE的长。

查看试题解析
23. 如图，在数轴上有两个长方形ABCD和EFGH，这两个长方形的宽都是2 $\sqrt{2}$ 个单位长度，长方形ABCD的长AD是4 $\sqrt{2}$ 个单位长度，长方形EFGH的长EH是8 $\sqrt{2}$ 个单位长度，点E在数轴上表示的数是5 $\sqrt{2}$ ，且E、D两点之间的距离为12 $\sqrt{2}$ 。

(1)、点H在数轴上表示的数是点，点A在数轴上表示的数是。

(2)、若线段AD的中点为M，线段EH上有一点N，EN= $\frac{1}{4}$ EH，M以每秒4个单位长度的速度向右匀速运动，N以每秒3个单位长度的速度向左运动，设运动的时间为x秒，问当x为多少时，原点O恰为线段MN的三等分点？

(3)、若线段AD的中点为M，线段EH上有一点N，EN= $\frac{1}{4}$ EH，长方形ABCD以每秒4个单位长度的速度向右匀速运动，长方形EFGH保持不动，设运动时间为t秒，是否存在一个t的值，使以M、N、F三点为顶点的三角形是直角三角形？若存在，求t的值；不存在，请说明理由。

查看试题解析