上海民办新竹园中2020年中考数学五模考试试卷
试卷更新日期:2020-04-01 类型:中考模拟
一、选择题(本大题共6小题,每题4分,满分24分)
-
1. 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=3:1,连接AE交BD于点F,则△DEF的面积与△BAF的面积之比为( )
 A、3:4 B、9:16 C、9:1 D、3:12. 在Rt△ABC中,∠C=90°,CD是高,如果AD=m,∠A=α,那么BC的长为( )A、m·tanα·cosα B、m·cotα·cosα C、 D、3. 如图,在△ABC中,点D是AB边上一点,若∠ACD=∠B,AD=1,AC=2,△ADC的面积为1,则△BCD的面积为( )
A、3:4 B、9:16 C、9:1 D、3:12. 在Rt△ABC中,∠C=90°,CD是高,如果AD=m,∠A=α,那么BC的长为( )A、m·tanα·cosα B、m·cotα·cosα C、 D、3. 如图,在△ABC中,点D是AB边上一点,若∠ACD=∠B,AD=1,AC=2,△ADC的面积为1,则△BCD的面积为( )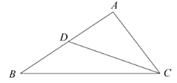 A、1 B、2 C、3 D、44. 下列说法中,错误的是( )A、长度为1的向量叫做单位向量 B、如果k≠0,且 ≠ ,那么k 的方向与 的方向相同 C、如果k=0或 = ,那么k = D、如果 = , = ,其中 是非零向量,那么 ∥5. 二次函数y=ax2+bx+c与一次函数y=ax+c的图像大致为( )A、
A、1 B、2 C、3 D、44. 下列说法中,错误的是( )A、长度为1的向量叫做单位向量 B、如果k≠0,且 ≠ ,那么k 的方向与 的方向相同 C、如果k=0或 = ,那么k = D、如果 = , = ,其中 是非零向量,那么 ∥5. 二次函数y=ax2+bx+c与一次函数y=ax+c的图像大致为( )A、 B、
B、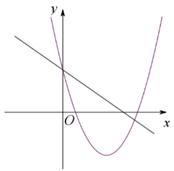 C、
C、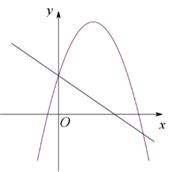 D、
D、 6. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE②△DFP∽△BPH③△PFD∽△PDB④DP2=PH·PC其中正确的有( )
6. 如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连接BD、DP,BD与CF相交于点H,给出下列结论:①BE=2AE②△DFP∽△BPH③△PFD∽△PDB④DP2=PH·PC其中正确的有( )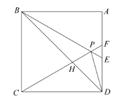 A、①②③④ B、②③ C、①②④ D、①③
A、①②③④ B、②③ C、①②④ D、①③二、填空题(本大题共12小题,每题4分,满分48分)
-
7. 计算: = 。
8. 已知线段a、b、c、d,如果 ,那么 =。9. 在比例尺为1:10000的地图上,一块面积为2平方厘米的区域表示的实际面积为平方米。10. 将抛物线y=x2沿x轴向右平移2个单位后所得的抛物线解析式是。11. 若点A(-3,y1)、B(0,y2)是二次函数y=-2(x-1)2+3图像上的点,那么y1与y2的大小关系是:y1 y2(填“>”,“<”或“=”)12. 如图,已知G是△ABC的重心,过点G作DE∥BC,分别交AB、AC于点D、E,那么用向量 表示向量 ,则 为。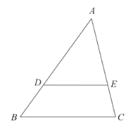 13. 如图,在△ABC中,M是AC中点,E是AB上一点,且AE= AB,连接EM并延长, 交BC的延长线于点D,则 =。
13. 如图,在△ABC中,M是AC中点,E是AB上一点,且AE= AB,连接EM并延长, 交BC的延长线于点D,则 =。 14. 一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3m,已知木箱高BE= m,斜面坡脚为30°,则木箱顶端E距离地面AC的高度EF为m。
14. 一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3m,已知木箱高BE= m,斜面坡脚为30°,则木箱顶端E距离地面AC的高度EF为m。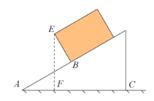 15. 一条斜坡长4米,高度为2米,那么这条斜坡的坡比i= 。16. 已知点P把线段AB分成AP和BP(AP>BP)两段,如果AP是AB和BP的比例中项,那么AP:AB的值为 。17. 在△ABC中,点D、E分别在边AB、AC上,∠AED=∠B,AB=6,BC=5,AC=4,如果四边形DBCE的周长为 ,那么AD的长为。18. 如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”,在Rt△ABC中,∠C=90°,若Rt△ABC是“好玩三角形”,则tanA= .
15. 一条斜坡长4米,高度为2米,那么这条斜坡的坡比i= 。16. 已知点P把线段AB分成AP和BP(AP>BP)两段,如果AP是AB和BP的比例中项,那么AP:AB的值为 。17. 在△ABC中,点D、E分别在边AB、AC上,∠AED=∠B,AB=6,BC=5,AC=4,如果四边形DBCE的周长为 ,那么AD的长为。18. 如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“好玩三角形”,在Rt△ABC中,∠C=90°,若Rt△ABC是“好玩三角形”,则tanA= .
三、解答题(本大题共7题,满分78分)(分值不明确)
-
19. 计算: ;20. 已知直线l1∥l2∥l3 , AG=1.2cm,BG=2.4cm,EF=3cm,CD=4cm,求CH、KF的值。
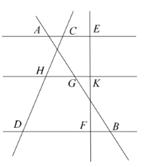 21. 如图,在△ABC中,BC=10,AB= ,∠ABC=45°
21. 如图,在△ABC中,BC=10,AB= ,∠ABC=45° (1)、求△ABC的面积;(2)、求cos∠C的值。22. 如图,A点、B点分别表示小岛码头、海岸码头的位置,离B点正东方向的7.00km处有一海岸瞭望塔C,又用经纬仪测出:A点分别在B点的北偏东57°处、在C点的东北方向。
(1)、求△ABC的面积;(2)、求cos∠C的值。22. 如图,A点、B点分别表示小岛码头、海岸码头的位置,离B点正东方向的7.00km处有一海岸瞭望塔C,又用经纬仪测出:A点分别在B点的北偏东57°处、在C点的东北方向。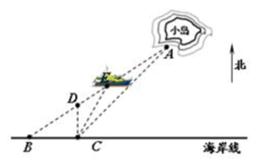
(注:tan33°≈0.65,sin33°≈0.54,cos33°≈0.84,结果精确到0.01km)
(1)、试求出小岛码头A点到海岸线BC的距离;(2)、有一观光客轮K从B至A方向沿直线航行;①某瞭望员在C处发现,客轮K刚好在正北方向的D处,试求出客轮驶出的距离BD的长;
②当客轮航行至E处时,发现E点在C的北偏东27°处,请求出E点到C点的距离;
23. 在△ABC中,AB=AC=4,D是AB上一点,且BD=1,连接CD,然后做∠CDE=∠B, 交平行于BC且过点A的直线于点E,DE交AC于点F,连接CE。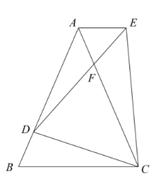 (1)、求证:△AFD∽△EFC;(2)、试求AE·BC的值。24. 二次函数y=-x2+bx+c的图像与x轴交于点B(-3,0),与y轴交于点C(0,-3)。
(1)、求证:△AFD∽△EFC;(2)、试求AE·BC的值。24. 二次函数y=-x2+bx+c的图像与x轴交于点B(-3,0),与y轴交于点C(0,-3)。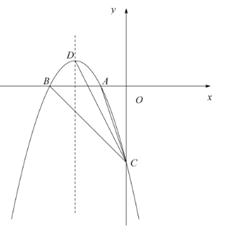 (1)、求二次函数解析式;(2)、设抛物线的顶点为D,与x轴的另一个交点为A,点P在抛物线的对称轴上,且∠APD=∠ACB,求点P的坐标;(3)、连接CD,求∠OCA与∠OCD的两个角的和的度数。25. 如图在Rt△ABC中,∠C=90°,AC=3,AB=5,点P从点C出发沿CA以每秒1个单位的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E。点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止。设点P、Q运动的时间是t秒(t>0)。
(1)、求二次函数解析式;(2)、设抛物线的顶点为D,与x轴的另一个交点为A,点P在抛物线的对称轴上,且∠APD=∠ACB,求点P的坐标;(3)、连接CD,求∠OCA与∠OCD的两个角的和的度数。25. 如图在Rt△ABC中,∠C=90°,AC=3,AB=5,点P从点C出发沿CA以每秒1个单位的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E。点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止。设点P、Q运动的时间是t秒(t>0)。 (1)、当t=2时,AP= , 点Q到AC的距离是;(2)、在点P从C向A运动的过程中,求△APQ的面积S与t的函数关系式;(不必写出t的取值范围)(3)、在点E从B向C运动的过程中,四边形QBED能否成为直角梯形?若能,求t的值。若不能,请说明理由;(4)、当DE经过点C时,请直接写出t的值。
(1)、当t=2时,AP= , 点Q到AC的距离是;(2)、在点P从C向A运动的过程中,求△APQ的面积S与t的函数关系式;(不必写出t的取值范围)(3)、在点E从B向C运动的过程中,四边形QBED能否成为直角梯形?若能,求t的值。若不能,请说明理由;(4)、当DE经过点C时,请直接写出t的值。