吉林省长春市2020年中考数学二模考试试卷
试卷更新日期：2020-04-01 类型：中考模拟
一、选择题（本大题共8小题，每小题3分，共24分）
-
1. -2020的绝对值是（ ）A、-2020 B、 C、 D、20202. 华为Mate20手机搭载了全球首款7纳米制程芯片，7纳米就是0.000 000 007米，数据0.000 000 007用科学记数法表示为（ ）A、7×10-7 B、0.7×10-8 C、0.7×10-7 D、7×10-93. 窗棂是中国传统木构建筑的框架结构设计，窗棂上雕刻有线槽和各种花纹，构成种类繁多的优美图案。下列表示我国古代窗棂样式结构的图案中，既是轴对称，又是中心对称的图形是（ ）A、
B、
C、
D、
4. 计算(x2y)3的结果是（ ）A、x6y3 B、x5y2 C、x5y D、x2y35. 若使 有意义，由x的取值范围是（ )A、x>3 B、x>-3 C、x≥3． D、x≥-36. 在数学活动也就是说上，九年级（1）班数学兴趣小组的同学们要测量某公园人工湖亭子A与它正东方向的主亭子B之间的距离，现测得亭子A位于点P北偏西30°方向，亭子B位于点P北偏东a方向，测得点P与亭子A之间的距离为200米，则亭子A与亭子B之间的距离为（ ）
A、 米 B、 米 C、 米 D、 米7. 如图，用三角板作△ABC的边AB上的高，下列三角板的摆放位置正确的是（ ）A、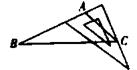
B、
C、
D、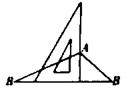
8. 如图，在平面直角坐标系中，Rt△ABC的顶点A，B分别在y轴、x轴上，OA=2，OB=1，斜边AC∥x轴，若反比例函数y= (k>0，x>0)的图象经过AC的中点D，则k的值为（ ）
A、4 B、5 C、6 D、8二、填空题(本大题共6小题，每小题3分，共18分)
-
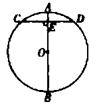
9. 因式分解：a3-16a=。10. 不等式组 的解集是。11. 用举反例的方法，说明命题“关于x的方程x2-4x+m=0一定有实数根”是假命题，则m的值可以是。12. 《九章算术》是我国古代数学的扛鼎之作，其中记载了这样一个问题：“今有圆材，埋在壁中，不知大小，以锯锯之，深一寸，铭道长一尺，问径几何？”。其大意为：如图AB为圆O的直径，弦CD⊥AB于点E，AE=1寸，CD=10寸，则直径AB的长为 寸。
13. 把正五边形和正六边形按如图所示方式放置，则∠a=。
14. 跳台滑雪是冬季奥运会比赛项目之一，运动员起跳后的飞行路线可以看作是抛物线的一部分，运动员起跳后的竖直高度y(单位；米)与水平距离a(单位：米)近似满足函数关系y=ax2+bx+c(a≠0) 。右图记录了某运动员起跳后的x与y的三组数据，根据上述函数模型和数据，可推断出该运动员起跳后飞行到最高点时，水平距离为米。
三、解答题(本大题共10小题，共78分)
-
15. 计算：16. 甲、乙两人做摸球游戏，在不透明的口袋里放人大小相同的两个黑球和两个白球，甲摸出两个球后放回并搅匀，乙再摸出两个球，若摸出一黑一白甲赢，若摸出两个相同颜色的乙赢．这个游戏公平吗？为什么？17. 在大城市，很多上班族选择“低碳出行”、电动车和共享单车成为他们的代步工具。某人去距离家8千米的单位上班，骑共享单车虽然比骑电动车多用20分钟，但却能强身健体．已知他骑电动车的速度是骑共享单车的1.5倍，求他骑共享单车从家到单位上班花费的时间。18. 中国古代有二十四节气歌：“春雨惊春清谷天，夏满芒夏暑相连，秋处露秋寒霜降，冬雪雪冬小大寒“它是为便于记忆我国古时历法中二十四节气而编成的小诗歌。流传至今，其中第一个”冬“是指立冬，为冬季的开始，但在气象学上的入冬日有是严格定义的，即日平均气温连续五天低于10℃，才算是进入冬天，其中5天中的第一天即为入冬日。
日平均气温是指一天24小时的平均值，气象上通常用一天中的2时、8时、14时、20时4个时刻的气温的平均值作为这一天的日平均气温（即4个气温相加除以4），结果保留一位小数。
下表是长春市某年10月6日至10月12日的气温纪录及日平均气温（单位：℃）
时间
2时
8时
14时
20时
平均气温
10月6日
2
8
18
13
10.3
10月7日
2
7
15
10
a
10月8日
2
7
14
9
8.0
10月9日
2
6
13
9
7.5
10月10日
3
5
9
6
5.8
10月11日
2
5
13
9
7.3
10月12日
4
8
17
13
10.5
根据以上材料解答下列问题：
(1)、求出10月7日的日平均气温a；(2)、采用适当的统计图将这7天的日平均气温的变化情况表示出来；(3)、请指出这一年的哪一天是长春市在气象学意义上的入冬日。19. 如图，△ABC是⊙O的内接三角形，∠ACB=45°，∠AOC=150°，过点C作⊙O的切线交AB的延长线于点D。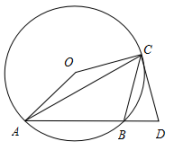
(1)、求证：CD=CB。(2)、如果⊙O的半径为2，求AC的长。20. 定义：我们把三边比为1： ： 的三角称为尾翼三角形。
(1)、请你在下面5×5和2×7的网格中分别画出面积最大的格点尾翼三角形。(2)、尾翼三角形的最大角为度。
21. 周末，甲、乙两名大学生骑自行车去距学校6000米的净月潭公园.两人同时从学校出发，以a米/分的速度匀速行驶.出发4.5分钟时，甲同学发现忘记带学生证，以1.5a米/分的速度按原路返回学校，取完学生证（在学校取学生证所用时间忽略不计），继续以返回时的速度追赶乙.甲追上乙后，两人以相同的速度前往净月潭.乙骑自行车的速度始终不变.设甲、乙两名大学生距学校的路程为s（米），乙同学行驶的时间为t（分），s与t之间的函数图象如图所示.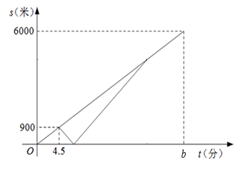
(1)、求a、b的值.(2)、求甲追上乙时，距学校的路程.(3)、当两人相距500米时，直接写出t的值是.22. 阅读下列材料，完成相应的任务。数学活动课上，老师提出如下问题：
如图①，在四边形ABCD中，AB⊥BC，DC⊥BC，AB=2，DC=4，BC=8，点P为BC边上的动点，求当BP的值是多少时，AP+DP有最小值，最小值是多少。
小丽和小明对老师提出的问题进行了合作探究：
小丽：设BP=x，则CP=8-x，
根据勾股定理，可得AP+DP=
但没有办法继续求解。
小明：利用轴对称作图，如图②，
作点A关于直线BC的对称点A'，连接A'D，与BC交于点P，
根据两点之间线段最短，将求AP+DP的最小值转化为求线段AD的长。
由△A‘BP∽△DCP，得
所以BP=
过点A'作A'H⊥DC，交DC的延长线于点H，
再由勾股定理，可得A'D= =10。
所以当BP= 时，AP+DP有最小值，最小值为10。
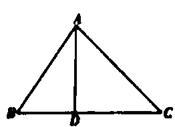图③任务：
(1)、类比探究：对于函数y= ，当x=时，y有最小值，最小值为。
(2)、应用拓展：如图③，若点D在BC上运动，AD上BC，AD=3，BC=5。连接AB，AC， 求△ABC周长的最小值。23. 综合与实践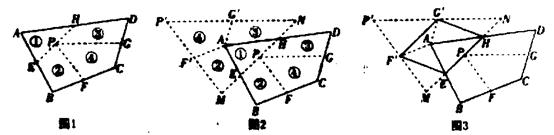
(1)、【动手操作】任意一个四边形ABCD通过剪裁，都可以拼接成一个三角形，方法如下：如图1．点E、F、G、H分别是边AB、BC、CD、DA的中点．连结EH，点P是线段EH的中点，连结PF、PG．沿线段EH、PF，PG剪开，将四边形ABCD分成①、②、③、④四部分，按如图所示的方式即可拼成一个无缝隙也不重叠的三角形P'MN。
在拼接过程中用到的图形的变换有。
A．轴对称 B．平移 C．中心对称 D．位似
(2)、【性质探究】如图3，连结EF'、F'G'、G'H，判断四边形EF'G'H的形状，并说明理由。(3)、【综合运用】若三角形P'MN是一个边长为4的正三角形，则四边形ABCD周长的最小值为。24. 如图①，在平面直角坐标系中，当线段AB与坐标轴不垂直时，以线段AB为斜边作Rt△ABC，且边BC⊥x轴，则称AC+BC的值为线段AB的直角距离，记作L(AB)；当线段AB与坐标轴垂直时，线段AB的直角距离不存在。
(1)、在平面直角坐标系中，A(1，4)，B(4，2)，求L(AB)。(2)、在平面直角坐标系中．点A与坐标原点重合．点B(x，y)，且L(AB)=2。①当点B(x：y)在第一象限时，易知AC=x，BC=y，由AC+BC=L(AB)，可得y与x之间的函数关系式为 ， 其中x的取值范围是。
(3)、在图②中画出这个函数的图象。②请模仿①的思考过程，分别探究点B在其它象限的情形，仍然在图②中分别画出点B在二、三、四象限时，y与x的函数图象。(不要求写出探究过程)
(4)、在平面直角坐标系中，点A(1，1），点B在抛物线y=a(x-h)2+5上，且2≤L(AB)≤4。①a= 时，直接写出h的取值范围。
②当h=0，且△ABC是等腰直角三角形时，直接写出a的取值范围。