上海市长宁区、金山区2020年中考数学一模考试试卷

试卷更新日期：2020-04-01 类型：中考模拟

进入出卷网下载

一、单选题

1. 下列函数中是二次函数的是（）

A、y＝ $\frac{2}{x^{2}}$ B、y＝（x+3）²﹣x² C、y＝ $\sqrt{x^{2} + 2 x - 1}$ D、y＝x（x﹣1）

查看试题解析
2. 如图，已知在平面直角坐标系xOy内有一点A（2，3），那么OA与x轴正半轴y的夹角α的余切值是（）

A、 $\frac{3}{2}$ B、 $\frac{2}{3}$ C、 $\frac{3 \sqrt{13}}{13}$ D、 $\frac{2 \sqrt{13}}{13}$

查看试题解析
3. 将抛物线y＝（x+1）²﹣3向右平移2个单位后得到的新抛物线的表达式为（）

A、y＝（x﹣1）²﹣3 B、y＝（x+3）²﹣3 C、y＝（x+1）²﹣1 D、y＝（x+1）²﹣5

查看试题解析
4. 下列命题正确是（）

A、如果| $\vec{a}$ |＝| $\vec{b}$ |，那么 $\vec{a}$ ＝ $\vec{b}$ B、如果 $\vec{a}$ 、 $\vec{b}$ 都是单位向量，那么 $\vec{a}$ ＝ $\vec{b}$ C、如果 $\vec{a}$ ＝k $\vec{b}$ （k≠0），那么 $\vec{a}$ ∥ $\vec{b}$ D、如果m＝0或 $\vec{a}$ ＝ $\vec{0}$ ，那么m $\vec{a}$ ＝0

查看试题解析
5. 已知在矩形ABCD中，AB＝5，对角线AC＝13．⊙C的半径长为12，下列说法正确是（）

A、⊙C与直线AB相交 B、⊙C与直线AD相切 C、点A在⊙C上 D、点D在⊙C内

查看试题解析
6. 如果点D、E ， F分别在△ABC的边AB、BC ， AC上，联结DE、EF ，且DE∥AC ，那么下列说法错误的是（）

A、如果EF∥AB ，那么AF：AC＝BD：AB B、如果AD：AB＝CF：AC ，那么EF∥AB C、如果△EFC∽△ABC ，那么 EF∥AB D、如果EF∥AB ，那么△EFC∽△BDE

查看试题解析

二、填空题

7. 计算：2（ $\vec{a}$ ﹣2 $\vec{b}$ ）+3（ $\vec{a}$ + $\vec{b}$ ）＝．

查看试题解析
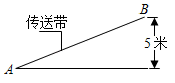
8. 如果 $\frac{x}{x - y}$ ＝ $\frac{3}{2}$ ，那么 $\frac{x}{y}$ 的值等于．

查看试题解析
9. 已知点P在线段AB上，且满足BP²＝AB•AP ，则 $\frac{BP}{AB}$ 的值等于．

查看试题解析
10. 已知抛物线y＝（1+a）x²的开口向上，则a的取值范围是．

查看试题解析
11. 抛物线y＝2x²﹣1在y轴左侧的部分是．（填“上升”或“下降”）

查看试题解析
12. 如果一条抛物线经过点A（2，5），B（﹣3，5），那么它的对称轴是直线．

查看试题解析
13. 如图，传送带把物体从地面送到离地面5米高的地方，如果传送带与地面所成的斜坡的坡度i＝1：2.4，那么物体所经过的路程AB为米．

查看试题解析
14. 如图，AC与BE交于点D ， ∠A＝∠E＝90°，若点D是线段AC的中点，且AB＝AC＝10．则BE的长等于．

查看试题解析
15. 如图，在Rt△ABC中，∠BAC＝90°，点G是重心，AC＝4，tan∠ABG＝ $\frac{1}{3}$ ，则BG的长是．

查看试题解析
16. 已知相交两圆的半径长分别为8与15，圆心距为17，则这两圆的公共弦长为．

查看试题解析
17. 如果直线l把△ABC分割后的两个部分面积相等，且周长也相等，那么就把直线l叫做△ABC的“完美分割线”，已知在△ABC中，AB＝AC ， △ABC的一条“完美分割线”为直线l ，且直线l平行于BC ，若AB＝2，则BC的长等于．

查看试题解析
18. 如图，在Rt△ABC中，∠ABC＝90°，AB＝2，BC＝4，点P在边BC上，联结AP ，将△ABP绕着点A旋转，使得点P与边AC的中点M重合，点B的对应点是点B′，则BB′的长等于．

查看试题解析

三、解答题

19. 计算： $\frac{\sin 30^{°} \cdot \tan^{2} 60^{°} - \cot 45^{°} + \cos 60^{°}}{\cos 30^{°} - \sin^{2} 45^{°}}$

查看试题解析
20. 如图，在梯形ABCD中，点E ， F分别在边AB ， CD上，AD∥EF∥BC ， EF与BD交于点G ， AD＝5，BC＝10， $\frac{AE}{EB}$ ＝ $\frac{2}{3}$ ．

(1)、求EF的长；

(2)、设 $\vec{A B}$ ＝ $\vec{a}$ ， $\vec{B C}$ ＝ $\vec{b}$ ，那么 $\vec{D B}$ ＝， $\vec{F C}$ ＝．（用向量 $\vec{a}$ 、 $\vec{b}$ 表示）

查看试题解析
21. 如图，已知AB是⊙O的弦，点C在⊙O上，且 $\overset{⌢}{A C} = \overset{⌢}{B C}$ ，联结AO ， CO ，并延长CO交弦AB于点D ， AB＝4 $\sqrt{3}$ ，CD＝6．

(1)、求∠OAB的大小；

(2)、若点E在⊙O上，BE∥AO ，求BE的长．

查看试题解析
22. 图1是一台实物投影仪，图2是它的示意图，折线O﹣A﹣B﹣C表示支架，支架的一部分O﹣A﹣B是固定的，另一部分BC是可旋转的，线段CD表示投影探头，OM表示水平桌面，AO⊥OM ，垂足为点O ，且AO＝7cm ， ∠BAO＝160°，BC∥OM ， CD＝8cm ．

将图2中的BC绕点B向下旋转45°，使得BCD落在BC′D′的位置（如图3所示），此时C′D′⊥OM ， AD′∥OM ， AD′＝16cm ，求点B到水平桌面OM的距离，（参考数据：sin70°≈0.94，cos70°≈0.34，cot70°≈0.36，结果精确到1cm）

查看试题解析
23. 如图，在△ABC中，点D、E分别在边AB、BC上，AE与CD交于点F ，若AE平分∠BAC ， AB•AF＝AC•AE ．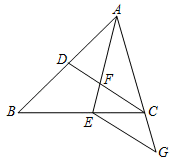

(1)、求证：∠AFD＝∠AEC；

(2)、若EG∥CD ，交边AC的延长线于点G ，求证：CD•CG＝FC•BD ．

查看试题解析
24. 如图，在平面直角坐标系xOy中，抛物线y＝ $\frac{1}{3}$ x²+mx+n经过点B（6，1），C（5，0），且与y轴交于点A ．

(1)、求抛物线的表达式及点A的坐标；

(2)、点P是y轴右侧抛物线上的一点，过点P作PQ⊥OA ，交线段OA的延长线于点Q ，如果∠PAB＝45°．求证：△PQA∽△ACB；

(3)、若点F是线段AB（不包含端点）上的一点，且点F关于AC的对称点F′恰好在上述抛物线上，求FF′的长．

查看试题解析
25. 如图，已知在Rt△ABC中，∠C＝90°，AC＝8，BC＝6，点P、Q分别在边AC、射线CB上，且AP＝CQ ，过点P作PM⊥AB ，垂足为点M ，联结PQ ，以PM、PQ为邻边作平行四边形PQNM ，设AP＝x ，平行四边形PQNM的面积为y ．

(1)、当平行四边形PQNM为矩形时，求∠PQM的正切值；

(2)、当点N在△ABC内，求y关于x的函数解析式，并写出它的定义域；

(3)、当过点P且平行于BC的直线经过平行四边形PQNM一边的中点时，直接写出x的值．

查看试题解析