上海市青浦区2020年中考数学一模考试试卷

试卷更新日期：2020-04-01 类型：中考模拟

进入出卷网下载

一、单选题

1. 如果两个相似三角形对应边之比是1∶2，那么它们的对应高之比是（）

A、1∶2； B、1∶4； C、1∶6； D、1∶8．

查看试题解析
2. 如图，DE∥AB ，如果CE∶AE =1∶2，DE=3，那么AB等于（）

A、6； B、9； C、12； D、13．

查看试题解析
3. 在Rt△ABC中，∠C=90º，AC=1，AB=3，则下列结论正确是（）

A、 $\sin B = \frac{\sqrt{2}}{4}$ ； B、 $\cos B = \frac{\sqrt{2}}{4}$ ； C、 $\tan B = \frac{\sqrt{2}}{4}$ ； D、 $\cot B = \frac{\sqrt{2}}{4}$ ．

查看试题解析
4. 已知非零向量 $\vec{a}$ 、 $\vec{b}$ ，且有 $\vec{a} = - 2 \vec{b}$ ，下列说法中，错误的是（）

A、 $| \vec{a} | = 2 | \vec{b} |$ ； B、 $\vec{a}$ ∥ $\vec{b}$ ； C、 $\vec{a}$ 与 $\vec{b}$ 方向相反； D、 $\vec{a} + 2 \vec{b} = 0$ ．

查看试题解析
5. 如图，在△ABC中，点D在边BC上，点G在线段AD上，GE∥BD ，且交AB于点E ， GF∥AC ，且交CD于点F ，则下列结论一定正确是（）

A、 $\frac{A E}{A B} = \frac{C F}{C D}$ ； B、 $\frac{A E}{E B} = \frac{D F}{F C}$ ； C、 $\frac{E G}{B D} = \frac{F G}{A C}$ ； D、 $\frac{A E}{A G} = \frac{A D}{A B}$ ．

查看试题解析
6. 抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 上部分点的横坐标x ，纵坐标y的对应值如下表，那么下列结论中正确是（）

x

…

-2

-1

0

1

2

…

y

…

0

4

6

6

4

…

A、 $a > 0$ ； B、 $b < 0$ ； C、 $c < 0$ ； D、 $a b c < 0$ ．

查看试题解析

二、填空题

7. 已知 $\frac{a}{b} = \frac{2}{5}$ ，那么 $\frac{a}{b - a}$ 的值为．

查看试题解析
8. 已知线段AB=2，P是AB的黄金分割点，且AP > BP ，那么AP= ．

查看试题解析
9. 已知向量 $\vec{a}$ 与单位向量 $\vec{e}$ 方向相反，且 $| \vec{a} | = 3$ ，那么 $\vec{a}$ =（用向量 $\vec{e}$ 的式子表示）

查看试题解析
10. 如果抛物线 $y = a x^{2} - 1$ 的顶点是它的最低点，那么 $a$ 的取值范围是．

查看试题解析
11. 如果点A（-3， $y_{1}$ ）和点B（-2， $y_{2}$ ）是抛物线 $y = x^{2} + a$ 上的两点，那么 $y_{1}$ $y_{2}$ ．（填“ $>$ ”、“=”、“ $<$ ”）．

查看试题解析
12. 某公司10月份的产值是100万元，如果该公司第四季度每个月产值的增长率相同，都为 $x （ x > 0)$ ，12月份的产值为 $y$ 万元，那么 $y$ 关于 $x$ 的函数解析式是．

查看试题解析
13. 在△ABC中，∠C=90°，如果tanB=2，AB=4，那么BC= ．

查看试题解析
14. 小明沿着坡度i=1∶2.5的斜坡前行了29米，那么他上升的高度是米．

查看试题解析
15. 已知点G是△ABC的重心，AB=AC=5,BC=8，那么AG= ．

查看试题解析
16. 如图，在菱形ABCD中，O、E分别是AC、AD的中点，联结OE ．如果AB=3，AC=4，那么cot∠AOE= ．

查看试题解析
17. 在方格纸中，每个小格的顶点叫做格点，以格点连线为边的三角形叫做格点三角形．如图，请在边长为1个单位的2×3的方格纸中，找出一个格点三角形DEF ．如果△DEF与△ABC相似（相似比不为1），那么△DEF的面积为．

查看试题解析
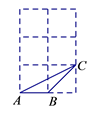18. 已知，在矩形纸片ABCD中，AB=5cm，点E、F分别是边AB、CD的中点，折叠矩形纸片ABCD ，折痕BM交AD边于点M ，在折叠的过程中，如果点A恰好落在线段EF上，那么边AD的长至少是cm．

查看试题解析

三、解答题

19. 计算： $3 \tan 30^{°} - \frac{1}{\cos 60^{°}} + \sqrt{8} \cos 45^{°} + \sqrt{{(1 - \tan 60^{°})}^{2}}$ ．

查看试题解析
20. 如图，在平行四边形ABCD中，E为DC上一点，AE与BD交于点F ， DE∶EC=2∶3．

(1)、求BF∶DF的值；

(2)、如果 $\vec{A D} = \vec{a}$ ， $\vec{A B} = \vec{b}$ ，试用 $\vec{a}$ 、 $\vec{b}$ 表示向量 $\vec{A F}$ ．

查看试题解析
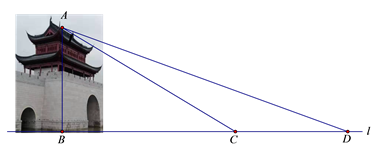
21. 如图，在Rt△ABC中，∠ACB=90º，AC=2，BC=3．点D为AC的中点，联结BD ，过点C作CG⊥BD ，交AC的垂线AG于点G ， GC分别交BA、BD于点F、E ．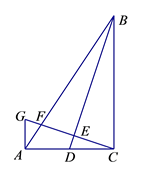

(1)、求GA的长；

(2)、求△AFC的面积．

查看试题解析
22. 水城门位于淀浦河和漕港河三叉口，是环城水系公园淀浦河梦蝶岛区域重要的标志性景观．在课外实践活动中，某校九年级数学兴趣小组决定测量该水城门的高．他们的操作方法如下：如图，先在D处测得点A的仰角为20°，再往水城门的方向前进13米至C处，测得点A的仰角为31°（点D、C、B在一直线上），求该水城门AB的高．（精确到0.1米）
（参考数据：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36，sin31°≈0.52，cos31°≈0.86，tan31°≈0.60）

查看试题解析
23. 已知：如图，在△ABC中，点D在边BC上，AE∥BC ， BE与AD、AC分别相交于点F、G ， $A F^{2} = F G \cdot F E$ ．

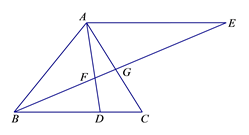(1)、求证：△CAD∽△CBG；

(2)、联结DG ，求证： $D G \cdot A E = A B \cdot A G$ ．

查看试题解析
24. 如图，在平面直角坐标系xOy中，抛物线 $y = x^{2} + b x + c$ 与x轴交于A、B两点，与y轴交于点C ，对称轴为直线x=2，点A的坐标为（1，0）．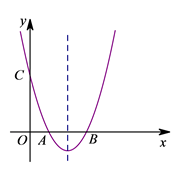

(1)、求该抛物线的表达式及顶点坐标；

(2)、点P为抛物线上一点（不与点A重合），联结PC ．当∠PCB=∠ACB时，求点P的坐标；

(3)、在（2）的条件下，将抛物线沿平行于 $y$ 轴的方向向下平移，平移后的抛物线的顶点为点D ，点P关于x轴的对应点为点Q ，当OD⊥DQ时，求抛物线平移的距离．

查看试题解析
25. 如图，在梯形ABCD中，AD∥BC ， BC=BD=10，CD=4，AD=6．点P是线段BD上的动点，点E、Q分别是线段DA、BD上的点，且DE=DQ=BP ，联结EP、EQ ．

(1)、求证：EQ∥DC；

(2)、如果△EPQ是以EQ为腰的等腰三角形，求线段BP的长；

(3)、当BP=m（0<m<5）时，求∠PEQ的正切值．（用含m的式子表示）

查看试题解析

x	…	-2	-1	0	1	2	…
y	…	0	4	6	6	4	…