上海市虹口区2020年中考数学一模考试试卷

试卷更新日期：2020-04-01 类型：中考模拟

进入出卷网下载

一、单选题

1. 若cosα＝ $\frac{1}{2}$ ，则锐角α的度数是（）

A、30° B、45° C、60° D、90°

查看试题解析
2. 在Rt△ABC中，∠C＝90°，如果BC＝2，tanB＝2，那么AC＝（）

A、1 B、4 C、 $\sqrt{5}$ D、2 $\sqrt{5}$

查看试题解析
3. 抛物线y＝3（x+1）²+1的顶点所在象限是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
4. 已知抛物线y＝x²经过A（﹣2，y₁）、B （1，y₂）两点，在下列关系式中，正确是（）

A、y₁＞0＞y₂ B、y₂＞0＞y₁ C、y₁＞y₂＞0 D、y₂＞y₁＞0

查看试题解析
5. 已知 $\vec{a}$ 、 $\vec{b}$ 和 $\vec{c}$ 都是非零向量，在下列选项中，不能判定 $\vec{a}$ ∥ $\vec{b}$ 的是（）

A、 $| \vec{a} | = | \vec{b} |$ B、 $\vec{a}$ ∥ $\vec{c}$ ， $\vec{b}$ ∥ $\vec{c}$ C、 $\vec{a}$ + $\vec{b}$ ＝0 D、 $\vec{a}$ + $\vec{b}$ ＝ $2 \vec{c}$ ， $\vec{a}$ ﹣ $\vec{b}$ ＝ $3 \vec{c}$

查看试题解析
6. 如图，点D是△ABC的边BC上一点，∠BAD＝∠C ， AC＝2AD ，如果△ACD的面积为15，那么△ABD的面积为（）

A、15 B、10 C、7.5 D、5

查看试题解析

二、填空题

7. 如果a：b＝2：3，且a+b＝10，那么a＝．

查看试题解析
8. 如果向量 $\vec{a}$ 、 $\vec{b}$ 和 $\vec{x}$ 满足关系式 $2 \vec{b} -3 (\vec{a} + \vec{x}) = 0$ ，那么用向量 $\vec{a}$ 、 $\vec{b}$ 表示向量 $\vec{x}$ ＝．

查看试题解析
9. 如果抛物线y＝（1﹣a）x²+1的开口向下，那么a的取值范围是．

查看试题解析
10. 沿着x轴正方向看，抛物线y＝﹣（x﹣1）²在对称轴侧的部分是下降的（填“左”、“右”）．

查看试题解析
11. 如果函数 $y = (m + 1) x^{m^{2} - m} +2$ 是二次函数，那么m＝．

查看试题解析
12. 如图，抛物线的对称轴为直线x＝1，点P、Q是抛物线与x轴的两个交点，点P在点Q的右侧，如果点P的坐标为（4，0），那么点Q的坐标为．

查看试题解析
13. 如图，点A（2，m）在第一象限，OA与x轴所夹的锐角为α，如果tanα＝ $\frac{3}{2}$ ．那么m＝．

查看试题解析
14. 已知△ABC∽△A₁B₁C₁ ，顶点A、B、C分别与A₁、B₁、C₁对应，AC＝12、A₁C₁＝8，△ABC的高AD为6，那么△A₁B₁C₁的高A₁D₁长为．

查看试题解析
15. 如图，在梯形AEFB中，AB∥EF ， AB＝6，EF＝10，点C、D分别在边AE、BF上且CD∥AB ，如果AC＝3CE ，那么CD＝．

查看试题解析
16. 公元三世纪，我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”，它由四个全等的直角三角形与中间的小正方形拼成的一个大正方形，如果小正方形面积是49，直角三角形中较小锐角θ的正切为 $\frac{5}{12}$ ，那么大正方形的面积是．

查看试题解析
17. 如图，在Rt△ABC中，∠C＝90°，AC＝1，BC＝2，点D为边AB上一动点，正方形DEFG的顶点E、F都在边BC上，联结BG ， tan∠DGB＝．

查看试题解析
18. 如图，在等腰梯形ABCD中，AD∥BC ， sinC＝ $\frac{4}{5}$ ，AB＝9，AD＝6，点E、F分别在边AB、BC上，联结EF ，将△BEF沿着EF所在直线翻折，使BF的对应线段B′F经过顶点A ， B′F交对角线BD于点P ，当B′F⊥AB时，AP的长为．

查看试题解析

三、解答题、

19. 计算： $\frac{4 \sin 30^{\circ}}{\cot 30^{\circ} - \tan 45^{\circ}} - \tan^{2} 60^{\circ}$

查看试题解析
20. 在平面直角坐标系中，将抛物线C₁：y＝x²﹣2x向左平移2个单位，向下平移3个单位得到新抛物线C₂ ．

(1)、求新抛物线C₂的表达式；

(2)、如图，将△OAB沿x轴向左平移得到△O′A′B′，点A（0，5）的对应点A′落在平移后的新抛物线C₂上，求点B与其对应点B′的距离．

查看试题解析
21. 如图，在Rt△ABC中，∠ABC＝90°，点G是Rt△ABC的重心，联结BG并延长交AC于点D ，过点G作GE⊥BC交边BC于点 E ．

(1)、如果 $\vec{A C} = \vec{a}$ ， $\vec{A B} = \vec{b}$ ， $\vec{a}$ 、 $\vec{b}$ 表示向量 $\vec{B G}$ ；

(2)、当AB＝12时，求GE的长．

查看试题解析
22. 某次台风来袭时，一棵笔直大树树干AB（假定树干AB垂直于水平地面）被刮倾斜7°（即∠BAB′＝7°）后折断倒在地上，树的顶部恰好接触到地面D处，测得∠CDA＝37°，AD＝5米，求这棵大树AB的高度．（结果保留根号）（参考数据：sin37≈0.6，cos37＝0.8，tan37≈0.75）

查看试题解析
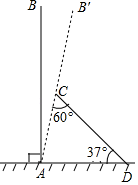23. 如图，在Rt△ABC中，∠ACB＝90°，点D是边BC的中点，联结AD ．过点C作CE⊥AD于点E ，联结BE ．

(1)、求证：BD²＝DE•AD；

(2)、如果∠ABC＝∠DCE ，求证：BD•CE＝BE•DE ．

查看试题解析
24. 在平面直角坐标系中，抛物线y＝﹣x²+bx+c与x轴交于A（﹣1，0）、B两点，与y轴交于点C （0，3），点P在该抛物线的对称轴上，且纵坐标为2 $\sqrt{3}$ ．

(1)、求抛物线的表达式以及点P的坐标；

(2)、当三角形中一个内角α是另一个内角β的两倍时，我们称α为此三角形的“特征角”．
①当D在射线AP上，如果∠DAB为△ABD的特征角，求点D的坐标；

②点E为第一象限内抛物线上一点，点F在x轴上，CE⊥EF ，如果∠CEF为△ECF的特征角，求点E的坐标．

查看试题解析
25. 如图，在Rt△ABC中，∠ACB＝90°，BC＝4，sin∠ABC＝ $\frac{3}{5}$ ，点D为射线BC上一点，联结AD ，过点B作BE⊥AD分别交射线AD、AC于点E、F ，联结DF ，过点A作AG∥BD ，交直线BE于点G ．

(1)、当点D在BC的延长线上时，如果CD＝2，求tan∠FBC；

(2)、当点D在BC的延长线上时，设AG＝x ， S_△_DAF＝y ，求y关于x的函数关系式（不需要写函数的定义域）；

(3)、如果AG＝8，求DE的长．

查看试题解析