上海松江区2020年中考数学一模考试试卷
试卷更新日期:2020-04-01 类型:中考模拟
一、单选题
-
1. 已知二次函数 的图像如图所示,那么下列判断正确( )
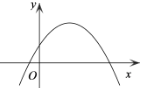 A、 , , B、 , , C、 , , D、 , ,2. 如果点A(1,3)、B(m , 3)是抛物线 上两个不同的点,那么m的值为( )A、2 B、3 C、4 D、53. 在以O为坐标原点的直角坐标平面内,有一点A(3,4),射线OA与x轴正半轴的夹角为 ,那么 的值为( )A、 B、 C、 D、4. 下列两个三角形不一定相似的是( )A、两条直角边的比都是 的两个直角三角形 B、腰与底的比都是 的两个等腰三角形 C、有一个内角为 的两个直角三角形 D、有一个内角为 的两个等腰三角形5. 如果 , ,且 ,下列结论正确是( )A、 B、 C、 与 方向相同 D、 与 方向相反6. 如图,两条宽度都为1的纸条,交叉重叠放在一起,它们的夹角为锐角 ,它们重叠部分(阴影部分)的面积是1.5,那么 的值为( )
A、 , , B、 , , C、 , , D、 , ,2. 如果点A(1,3)、B(m , 3)是抛物线 上两个不同的点,那么m的值为( )A、2 B、3 C、4 D、53. 在以O为坐标原点的直角坐标平面内,有一点A(3,4),射线OA与x轴正半轴的夹角为 ,那么 的值为( )A、 B、 C、 D、4. 下列两个三角形不一定相似的是( )A、两条直角边的比都是 的两个直角三角形 B、腰与底的比都是 的两个等腰三角形 C、有一个内角为 的两个直角三角形 D、有一个内角为 的两个等腰三角形5. 如果 , ,且 ,下列结论正确是( )A、 B、 C、 与 方向相同 D、 与 方向相反6. 如图,两条宽度都为1的纸条,交叉重叠放在一起,它们的夹角为锐角 ,它们重叠部分(阴影部分)的面积是1.5,那么 的值为( )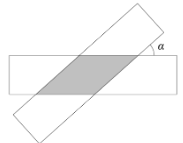 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
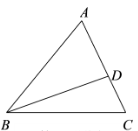
7. 已知: ,那么 .8. 已知线段a是线段b、c的比例中项,如果 , ,那么 .9. 若两个相似三角形的面积比为 ,则它们的相似比为 .10. 已知点 是线段 上的黄金分割点, ,且 ,那么 .11. 已知Rt△ABC中,若∠C=90°,AC=3,BC=2,则∠A的余切值为 .12. 已知二次函数 图像的对称轴为直线 ,则 .(填“>”或“<”)13. 在直角坐标平面中,将抛物线 先向上平移1个单位,再向右平移1个单位,那么平移后的抛物线表达式是 .14. 如图,已知D是△ABC的边AC上一点,且AD=2DC . 如果 , ,那么向量 关于 、 的分解式是 .
 15. 如图,在正方形网格中,点A , B , C是小正方形的顶点,那么tan∠BAC的值为 .
15. 如图,在正方形网格中,点A , B , C是小正方形的顶点,那么tan∠BAC的值为 .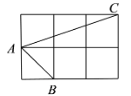 16. 如图,某幢楼的楼梯每一级台阶的高度为20厘米,宽度为30厘米.那么斜面AB的坡度为 .
16. 如图,某幢楼的楼梯每一级台阶的高度为20厘米,宽度为30厘米.那么斜面AB的坡度为 .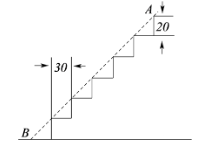 17. 以一个等腰直角三角形的腰为边分别向形外做等边三角形,我们把这两个等边三角形重心之间的距离称作这个等腰直角三角形的“肩心距”.如果一个等腰直角三角形的腰长为2,那么它的“肩心距” .18. 如图,矩形ABCD中,AD=1,AB= .将矩形ABCD绕着点B顺时针旋转90°得到矩形 .联结 ,分别交边CD , 于E、F . 如果AE= ,那么 = .
17. 以一个等腰直角三角形的腰为边分别向形外做等边三角形,我们把这两个等边三角形重心之间的距离称作这个等腰直角三角形的“肩心距”.如果一个等腰直角三角形的腰长为2,那么它的“肩心距” .18. 如图,矩形ABCD中,AD=1,AB= .将矩形ABCD绕着点B顺时针旋转90°得到矩形 .联结 ,分别交边CD , 于E、F . 如果AE= ,那么 = .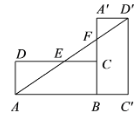
三、解答题
-
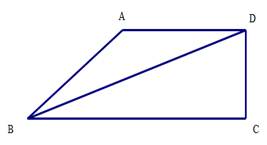
19. 计算:20. 已知二次函数 .(1)、将函数 的解析式化为 的形式,并指出该函数图象顶点B坐标;(2)、在平面直角坐标系中xOy中,设抛物线 与y轴交点为C , 抛物线的对称轴与x轴交点为A.求四边形OABC的面积.21. 如图:在梯形ABCD中,AD∥BC , ∠C=90°,AD=AB=13,BD=24.求边DC的长.
 22. 如图,小岛A在港口P的南偏西45°方向上,一艘船从港口P , 沿着正南方向,以每小时12海里的速度航行,1小时30分钟后到达B处,在B处测得小岛A在它的南偏西60°的方向上.小岛A离港口P有多少海里?
22. 如图,小岛A在港口P的南偏西45°方向上,一艘船从港口P , 沿着正南方向,以每小时12海里的速度航行,1小时30分钟后到达B处,在B处测得小岛A在它的南偏西60°的方向上.小岛A离港口P有多少海里?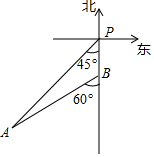 23. 已知:如图,点D、F在△ABC边AC上,点E在边BC上,且DE∥AB , .
23. 已知:如图,点D、F在△ABC边AC上,点E在边BC上,且DE∥AB , . (1)、求证:EF∥BD;(2)、如果 ,求证: .24. 如图,已知抛物线y= x2+bx+c过点A(3, 0)、点B(0, 3).点M(m , 0)在线段OA上(与点A、O不重合),过点M作x轴的垂线与线段AB交于点P , 与抛物线交于点Q , 联结BQ .
(1)、求证:EF∥BD;(2)、如果 ,求证: .24. 如图,已知抛物线y= x2+bx+c过点A(3, 0)、点B(0, 3).点M(m , 0)在线段OA上(与点A、O不重合),过点M作x轴的垂线与线段AB交于点P , 与抛物线交于点Q , 联结BQ .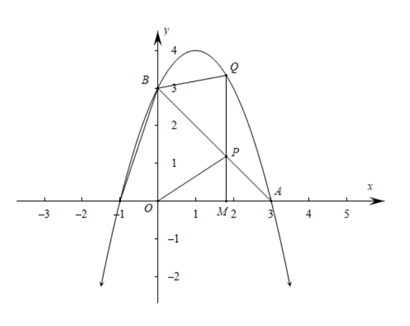 (1)、求抛物线表达式;(2)、联结OP , 当∠BOP=∠PBQ时,求PQ的长度;(3)、当△PBQ为等腰三角形时,求m的值.25. 已知tan∠MON=2,矩形ABCD的边AB在射线OM上,AD=2,AB=m,CF⊥ON , 垂足为点F.(1)、如图(1),作AE⊥ON , 垂足为点E. 当m=2时,求线段EF的长度;
(1)、求抛物线表达式;(2)、联结OP , 当∠BOP=∠PBQ时,求PQ的长度;(3)、当△PBQ为等腰三角形时,求m的值.25. 已知tan∠MON=2,矩形ABCD的边AB在射线OM上,AD=2,AB=m,CF⊥ON , 垂足为点F.(1)、如图(1),作AE⊥ON , 垂足为点E. 当m=2时,求线段EF的长度;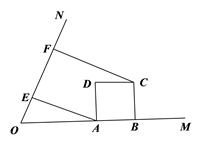
图(1)
(2)、如图(2),联结OC , 当m=2,且CD平分∠FCO时,求∠COF的正弦值;
图(2)
(3)、如图(3),当△AFD与△CDF相似时,求m的值.
图(3)