上海市杨浦区2019年中考数学三模考试试卷

试卷更新日期：2020-04-01 类型：中考模拟

进入出卷网下载

一、单选题

1. 在实数|﹣3|，﹣2，0，π中，最小的数是（）

A、|﹣3| B、﹣2 C、0 D、π

查看试题解析
2. 下列各式的变形中，正确是（）

A、(－x－y)(－x＋y)＝x²－y² B、 $\frac{1}{x}$ －x＝ $\frac{1 - x}{x}$ C、x²－4x＋3＝(x－2)²＋1 D、x÷(x²＋x)＝ $\frac{1}{x}$ ＋1

查看试题解析
3. 将样本容量为100的样本编制成组号①～⑧的八个组，简况如表所示：
组号
①
②
③
④
⑤
⑥
⑦
⑧
频数
14
11
12
13
■
13
12
10
那么第⑤组的频率是（　　）

A、14 B、15 C、0.14 D、0.15

查看试题解析
4. 在平面直角坐标系中，点A的坐标是(﹣1，2)，将点A向右平移4个单位，得到点A′，再作点A′关于y轴的对称点，得到点A″，则点A″的坐标是（）

A、(3，2) B、(3，﹣2) C、(﹣3，﹣2) D、(﹣3，2)

查看试题解析
5. 下列说法中正确是（）

A、三角形三条角平分线的交点到三个顶点的距离相等 B、三角形三条角平分线的交点到三边的距离相等 C、三角形三条中线的交点到三个顶点的距离相等 D、三角形三条中线的交点到三边的距离相等

查看试题解析
6. 如图，在四边形ABCD中，AC与BD相交于点O ， ∠BAD＝90°，BO＝DO ，那么添加下列一个条件后，仍不能判定四边形ABCD是矩形的是（）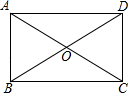

A、∠ABC＝90° B、∠BCD＝90° C、AB＝CD D、AB∥CD

查看试题解析

二、填空题

7. 计算：(﹣2)⁹÷2⁷＝．

查看试题解析
8. 计算： $\sqrt{18} + \sqrt{32}$ ＝．

查看试题解析
9. 如果关于x的一元二次方程x²﹣6x+m﹣1＝0有两个不相等的实数根，那么m的取值范围是．

查看试题解析
10. 函数y= $\sqrt{2 - x} + \frac{1}{x + 1}$ 中自变量x的取值范围是．

查看试题解析
11. 一次函数y＝kx+b(k≠0)的图象如图所示，如果y≤0，那么x的取值范围．

查看试题解析
12. 某班10名学生校服尺寸与对应人数如图所示，那么这10名学生校服尺寸的中位数为cm ．

查看试题解析
13. 在“石头、剪刀、布”的游戏中，两人打出相同标识手势的概率是．

查看试题解析
14. 某大型超市从生产基地以每千克a元的价格购进一种水果m千克，运输过程中重量损失了10%，超市在进价的基础上増加了30%作为售价，假定不计超市其他费用，那么售完这种水果，超市获得的利润是元(用含m、a的代数式表示)

查看试题解析
15. 如图，已知在▱ABCD中，E是边AB的中点，DE与对角线AC相交于点F ．如果 $\vec{A B} = \vec{a}$ ， $\vec{A D} = \vec{b}$ ，那么 $\vec{D F}$ ＝(用含 $\vec{a}$ 、 $\vec{b}$ 的式子表示)．

查看试题解析
16. 小明在空中距地面30米的热气球上看向地面上的一个雕塑，如果此时热气球与雕塑相距50米，那么小明看雕塑时的俯角约等于度(备用数据：sin37°＝cos53°≈0.6)

查看试题解析
17. 如图，正五边形ABCDE的边长为2，分别以点C、D为圆心，CD长为半径画弧，两弧交于点F，则 $\overset{⌢}{B F}$ 的长为.

查看试题解析
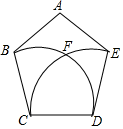18. 如图，矩形ABCD中，AB＝5，BC＝12，将矩形绕着点D顺时针旋转，当点C落在对角线BD上的点E处时，点A、B分别落在点G、F处，那么AG：BF：CE＝．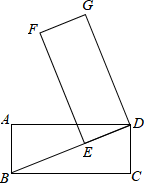

查看试题解析

三、解答题

19. 先化简，再计算： $\frac{x^{2} - x - 2}{x} \cdot \frac{1}{x - 2} - \frac{2 x + 2}{x^{2} + x}$ ，其中x＝ $\sqrt{2} + 1$ ．

查看试题解析
20. 已知：二次函数y＝2x²+bx+c的图象经过点A(1，0)，B(2，3)．求：这个二次函数的解析式，及这个函数图象的对称轴．

查看试题解析
21. 如图，已知某船向正东方向航行，在点A处测得某岛C在其北偏东60°方向上，前进8海里处到达点B处，测得岛C在其北偏东30°方向上．已知岛C周围6海里内有一暗礁，问：如果该船继续向东航行，有无触礁危险？请说明你的理由．

查看试题解析
22. 在女子800米耐力测试中，某考点同时起跑的小莹和小梅所跑的路程S(米)与所用时间t(秒)之间的函数关系分別如图中线段OA和折线OBCD所示．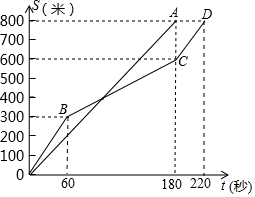

(1)、谁先到终点，当她到终点时，另一位同学离终点多少米？(请直接写出答案)

(2)、起跑后的60秒内谁领先？她在起跑后几秒时被追及？请通过计算说明．

查看试题解析
23. 已知，在△ACB和△DCE中，∠ACB＝∠DCE＝90°，AC＝BC ， DC＝EC ， M为DE的中点，联结BE ．

(1)、如图1，当点A、D、E在同一直线上，联结CM ，求证：CM＝ $\frac{A E}{2} - \frac{B E}{2}$ ；

(2)、如图2，当点D在边AB上时，联结BM ，求证：BM²＝( $\frac{A D}{2}$ )²+( $\frac{B D}{2}$ )² ．

查看试题解析
24. 在平面直角坐标系xOy中，第一象限内的点P在直线y＝ $\frac{1}{2}$ x上，过点P的直线交x轴正半轴于点A ，交直线y＝3x于点B ，点B在第一象限内．

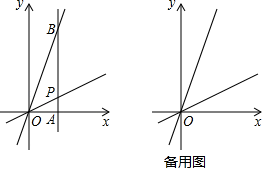(1)、如图1，当∠OAB＝90°时，求 $\frac{B P}{A P}$ 的值；

(2)、当点A的坐标为(6，0)，且BP＝2AP时，将过点A的抛物线y＝﹣x²+mx上下方平移，使它过点B ，求平移的方向和距离．

查看试题解析
25. △ABC中，∠ACB＝90°，tanB＝ $\frac{3}{4}$ ，AB＝5，点O为边AB上一动点，以O为圆心，OB为半径的圆交射线BC于点E ，以A为圆心，OB为半径的圆交射线AC于点G ．

(1)、如图1，当点E、G分别在边BC、AC上，且CE＝CG时，请判断圆A与圆O的位置关系，并证明你的结论；

(2)、当圆O与圆A存在公共弦MN时(如图2)，设OB＝x ， MN＝y ，求y关于x的函数解析式，并写出定义域；

(3)、设圆A与边AB的交点为F ，联结OE、EF ，当△OEF为以OE为腰的等腰三角形时，求圆O的半径长．

查看试题解析

组号	①	②	③	④	⑤	⑥	⑦	⑧
频数	14	11	12	13	■	13	12	10