上海市宝山区2019年中考数学一模考试试卷

试卷更新日期：2020-04-01 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图，已知 $A B / / C D / / E F$ ， $B D ： D F = 1 ： 2$ ，那么下列结论中，正确是（）

A、 $A C ： A E = 1 ： 3$ B、 $C E ： E A = 1 ： 3$ C、 $C D ： E F = 1 ： 2$ D、 $A B ： E F = 1 ： 2$

查看试题解析
2. 下列命题中，正确是（）

A、两个直角三角形一定相似 B、两个矩形一定相似 C、两个等边三角形一定相似 D、两个菱形一定相似

查看试题解析
3. 已知二次函数y＝ax²﹣1的图象经过点（1，﹣2），那么a的值为（）

A、a＝﹣2 B、a＝2 C、a＝1 D、a＝﹣1

查看试题解析
4. 如图，直角坐标平面内有一点 $P (2 ， 4)$ ，那么 $O P$ 与 $x$ 轴正半轴的夹角 $α$ 的余切值为（）

A、2 B、 $\frac{1}{2}$ C、 $\frac{\sqrt{5}}{5}$ D、 $\sqrt{5}$

查看试题解析
5. 设 $m, n$ 为实数，那么下列结论中错误的是（）

A、 $m （ n \vec{a} ）＝（ m n ） \vec{a}$ B、 $（ m + n ） \vec{a} ＝ m \vec{a} + n \vec{a}$ C、 $m （ \vec{a} + \vec{b} ）＝ m \vec{a} + m \vec{b}$ D、若 $m \vec{a} = \vec{0}$ ，那么 $\vec{a} = \vec{0}$

查看试题解析
6. 若⊙A的半径为5，圆心A的坐标是（1，2），点P的坐标是（5，2），那么点P的位置为（）

A、在⊙A内 B、在⊙A上 C、在⊙A外 D、不能确定

查看试题解析

二、填空题

7. 抛物线 $y = x^{2} - 1$ 的顶点坐标是.

查看试题解析
8. 将二次函数 $y = 2 x^{2}$ 的图象向右平移3个单位，所得图象的对称轴为.

查看试题解析
9. 请写出一个开口向下，且经过点 $(0, 2)$ 的二次函数解析式.

查看试题解析
10. 若 $2 | \vec{a} | = 3$ ，那么 $3 | \vec{a} | =$ .

查看试题解析
11. 甲、乙两地的实际距离为500千米，甲、乙两地在地图上的距离为10 cm，那么地图上距离为4.5 cm的两地之间的实际距离为千米．

查看试题解析
12. 如果两个相似三角形的周长的比等于1：4，那么它们的面积的比等于．

查看试题解析
13. Rt△ $A B C$ 中， $∠ C = 90 °$ ， $A B = 2 A C$ ，那么 $\sin B =$ .

查看试题解析
14. 直角三角形的重心到直角顶点的距离为4 $c m$ ，那么该直角三角形的斜边长为.

查看试题解析
15. 如图，四边形 $A B C D$ 中， $A B$ ∥ $C D$ ，点 $E$ 在 $C B$ 延长线上， $∠ A B D = ∠ C E A$ ，若3AE=2BD，BE=1，那么DC=.

查看试题解析
16. ⊙O的直径AB＝6，C在AB延长线上，BC＝2，若⊙C与⊙O有公共点，那么⊙C的半径r的取值范围是．

查看试题解析
17. 我们将等腰三角形腰长与底边长的差的绝对值称为该三角形的“边长正度值”，若等腰三角形腰长为5，“边长正度值”为3，那么这个等腰三角形底角的余弦值等于．

查看试题解析
18. 如图，Rt△ $A B C$ 中， $∠ A C B = 90 °$ ， $A C = 4$ ， $B C = 5$ ，点 $P$ 为 $A C$ 上一点，将△ $B C P$ 沿直线 $B P$ 翻折，点 $C$ 落在 $C^{'}$ 处，连接 $A C^{'}$ ，若 $A C^{'}$ ∥ $B C$ ，那么 $C P$ 的长为.

查看试题解析

三、解答题

19. 计算： $\sin 30 ° \cdot \tan 30 ° + \cos 60 ° \cdot \cot 30 °$ .

查看试题解析
20. 已知：如图，在△ABC中，AB＝AC，点E、F在边BC上，∠EAF＝∠B．求证：BF•CE＝AB² ．

查看试题解析
21. 如图，已知，△ $A B C$ 中，点 $D$ 、 $E$ 分别在 $A B$ 、 $A C$ 上， $A B = 9$ ， $A C = 6$ ， $A D = 2$ ， $A E = 3$

(1)、求 $\frac{D E}{B C}$ 的值；

(2)、设 $\vec{A B} = \vec{a}$ ， $\vec{A C} = \vec{b}$ ，求 $\vec{D E}$ .（用含 $\vec{a}$ 、 $\vec{b}$ 的式子表示）

查看试题解析
22. 如图，已知：Rt△ABC中，∠ACB＝90°，点E为AB上一点，AC＝AE＝3，BC＝4，过点A作AB的垂线交射线EC于点D ，延长BC交AD于点F ．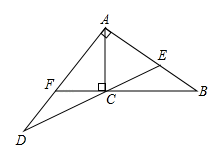

(1)、求CF的长；

(2)、求∠D的正切值．

查看试题解析
23. 地铁10号线某站点出口横截面平面图如图所示，电梯AB的两端分别距顶部9.9米和2.4米，在距电梯起点A端6米的P处，用1.5米的测角仪测得电梯终端B处的仰角为14°，求电梯AB的坡度与长度．
参考数据：sin14°≈0.24，tan14°≈0.25，cos14°≈0.97．

查看试题解析
24. 如图，已知：二次函数y＝x²+bx的图象交x轴正半轴于点A ，顶点为P ，一次函数y＝ $\frac{1}{2}$ x﹣3的图象交x轴于点B ，交y轴于点C ， ∠OCA的正切值为 $\frac{2}{3}$ ．

(1)、求二次函数的解析式与顶点P坐标；

(2)、将二次函数图象向下平移m个单位，设平移后抛物线顶点为P′，若S_△_ABP＝S_△_BCP ，求m的值．

查看试题解析
25. 如图，已知：梯形ABCD中，∠ABC＝90°，∠DAB＝45°，AB∥DC ， DC＝3，AB＝5，点P在AB边上，以点A为圆心AP为半径作弧交边DC于点E ，射线EP于射线CB交于点F ．

(1)、若AP $= \sqrt{13}$ ，求DE的长；

(2)、联结CP ，若CP＝EP ，求AP的长；

(3)、线段CF上是否存在点G ，使得△ADE与△FGE相似？若相似，求FG的值；若不相似，请说明理由．

查看试题解析