上海嘉定区2019年中考数学一模考试试卷
试卷更新日期:2020-04-01 类型:中考模拟
一、单选题
-
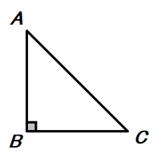
1. 下列选项中的两个图形一定相似的是. ( )A、两个等腰三角形 B、两个矩形 C、两个菱形 D、两个正五边形.2. 在Rt△ABC中,∠C=90°,AB=10,AC=8.下列四个选项,不符合题意是( )A、sinA= B、cosA= C、tanA= D、cotA=3. 如果A(-2,n),B(2,n),C(4,n+12)这三个点都在同一个函数的图象上,那么这个函数的解析式可能是 ( )A、 B、 C、 D、4. 如图,在平行四边形ABCD中,设 , ,那么向量 可以表示为. ( )
 A、 B、 C、 D、5. 三角形的重心是( )A、三角形三条边上中线的交点 B、三角形三条边上高线的交点 C、三角形三条边垂直平分线的交点 D、三角形三条内角平行线的交点6. 下列四个选项中的表述,一定正确是( )A、经过半径上一点且垂直于这条半径的直线是圆的切线; B、经过半径的端点且垂直于这条半径的直线是圆的切线; C、经过半径的外端且垂直于这条半径的直线是圆的切线; D、经过一条弦的外端且垂直于这条半径的直线是圆的切线.
A、 B、 C、 D、5. 三角形的重心是( )A、三角形三条边上中线的交点 B、三角形三条边上高线的交点 C、三角形三条边垂直平分线的交点 D、三角形三条内角平行线的交点6. 下列四个选项中的表述,一定正确是( )A、经过半径上一点且垂直于这条半径的直线是圆的切线; B、经过半径的端点且垂直于这条半径的直线是圆的切线; C、经过半径的外端且垂直于这条半径的直线是圆的切线; D、经过一条弦的外端且垂直于这条半径的直线是圆的切线.二、填空题
-
7. 如果2a=3b,那么 .8. 如果将一个三角形保持形状不变但周长扩大为原三角形周长的9倍,那么扩大后的三角形面积为原三角形面积的倍.9. 在某一时刻测得一根高为1.8m的竹竿的影长为0.9m,如果同时同地测得一栋的影长为27m,那么这栋楼的高度为m10. 在△ABC中,D、E分别是边AB、AC上的点,如果AD=2,DB=1,AE=4,EC=2,那么 的值为
 11. 抛物线 的顶点坐标为12. 如果抛物线 的对称轴为y轴,那么实数b的值等于13. 将抛物线 向右平移两个单位后,所得抛物线的表达式为14. 已知抛物线 经过点 和 ,那么y1y2(从“>”或“<”或“=”选择)15. 如图,有一个斜坡AB,坡顶B离地面的高度BC为30m,斜坡的坡度i=1:2.5,那么该斜坡的水平距离AC的长m
11. 抛物线 的顶点坐标为12. 如果抛物线 的对称轴为y轴,那么实数b的值等于13. 将抛物线 向右平移两个单位后,所得抛物线的表达式为14. 已知抛物线 经过点 和 ,那么y1y2(从“>”或“<”或“=”选择)15. 如图,有一个斜坡AB,坡顶B离地面的高度BC为30m,斜坡的坡度i=1:2.5,那么该斜坡的水平距离AC的长m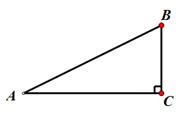 16. 如果正多边形的边数是n(n≥3),它的中心角是 °,那么 关于n的函数解析式是17. 如图, 的半径长为5cm, 内接于 ,圆心O在 的内部,如果 , cm,那么 的面积为cm
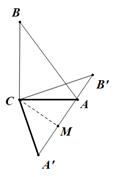
16. 如果正多边形的边数是n(n≥3),它的中心角是 °,那么 关于n的函数解析式是17. 如图, 的半径长为5cm, 内接于 ,圆心O在 的内部,如果 , cm,那么 的面积为cm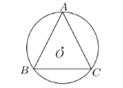 18. 在 中, , , ,把 绕着点C按照顺时针的方向旋转,将A、B的对应点分别记为点 、 ,如果 恰好经过点A,那么点A与点 的距离为
18. 在 中, , , ,把 绕着点C按照顺时针的方向旋转,将A、B的对应点分别记为点 、 ,如果 恰好经过点A,那么点A与点 的距离为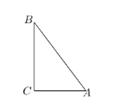
三、解答题
-
19. 计算:2cos30°+tan45°-2sin30°-cot30°20. 已知不等臂跷跷板AB长为3米,跷跷板AB的支撑点O到地面上的点H的距高OH=0.6米。当跷跷板AB的一个端点A碰到地面时,AB与地面上的直线AH的夹角∠OAH的度数为30°.
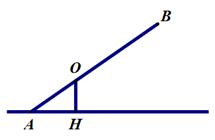
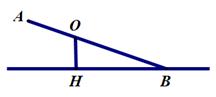 (1)、当AB的另一个端点B碰到地面时(如图),跷跷板AB与直线BH的夹角∠ABH的正弦值是多少?(2)、当AB的另一个端点B碰到地面时(如右图),点A到直线BH的距离是多少米?21. 如图,在⊙O中,AB、CD是两条弦,⊙O的半径长为rcm,弧AB的长度为 cm,弧CD的长度为 cm(温馨提醒:弧的度数相等,弧的长度相等,弧相等,有联系也有区别) 当 = 时,求证:AB=CD
(1)、当AB的另一个端点B碰到地面时(如图),跷跷板AB与直线BH的夹角∠ABH的正弦值是多少?(2)、当AB的另一个端点B碰到地面时(如右图),点A到直线BH的距离是多少米?21. 如图,在⊙O中,AB、CD是两条弦,⊙O的半径长为rcm,弧AB的长度为 cm,弧CD的长度为 cm(温馨提醒:弧的度数相等,弧的长度相等,弧相等,有联系也有区别) 当 = 时,求证:AB=CD 22. 如图,海中有一个小岛A,该岛的四周10海里的范围内有暗礁,有一货轮在海面上由西向东航行,到达B处时,该货轮位于小岛南偏西60°的方向上,再往东行驶20海里后到达小岛的南偏西30°的方向上的C处,如果货轮继续向东航行,是否会有触礁危险?请通过计算说明:
22. 如图,海中有一个小岛A,该岛的四周10海里的范围内有暗礁,有一货轮在海面上由西向东航行,到达B处时,该货轮位于小岛南偏西60°的方向上,再往东行驶20海里后到达小岛的南偏西30°的方向上的C处,如果货轮继续向东航行,是否会有触礁危险?请通过计算说明: 23. 已知:如图,在△ABC中,点D,E分别在边AB、 AC上,DE∥BC,∠ABE=∠C,
23. 已知:如图,在△ABC中,点D,E分别在边AB、 AC上,DE∥BC,∠ABE=∠C,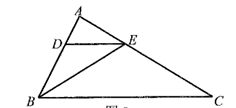 (1)、求证:(2)、当BE平分∠ABC时,求证:24. 在平面直角坐标系xOy中,将点 定义为点 的“关联点”. 已知点 在函数 的图像上,将点A的“关联点”记为点 .
(1)、求证:(2)、当BE平分∠ABC时,求证:24. 在平面直角坐标系xOy中,将点 定义为点 的“关联点”. 已知点 在函数 的图像上,将点A的“关联点”记为点 .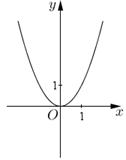 (1)、请在如图基础上画出函数 的图像,简要说明画图方法;(2)、如果点 在函数 的图像上,求点 的坐标;(3)、将点 称为点 的“待定关联点”(其中 ),如果点 的“待定关联点” 在函数 的图像上,试用含 的代数式表示点 的坐标.25. 已知:点P在△ABC内,且满足∠APB=∠APC(如下图),∠APB+∠BAC=180°,
(1)、请在如图基础上画出函数 的图像,简要说明画图方法;(2)、如果点 在函数 的图像上,求点 的坐标;(3)、将点 称为点 的“待定关联点”(其中 ),如果点 的“待定关联点” 在函数 的图像上,试用含 的代数式表示点 的坐标.25. 已知:点P在△ABC内,且满足∠APB=∠APC(如下图),∠APB+∠BAC=180°,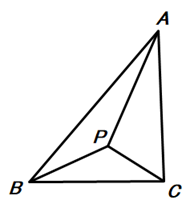 (1)、求证:△PAB∽△PCA:(2)、如下图,如果∠APB=120°,∠ABC=90°求 的值;
(1)、求证:△PAB∽△PCA:(2)、如下图,如果∠APB=120°,∠ABC=90°求 的值; (3)、如图,当∠BAC=45°,△ABC为等腰三角形时,求tan∠PBC的值.
(3)、如图,当∠BAC=45°,△ABC为等腰三角形时,求tan∠PBC的值.