黑龙江省哈尔滨市道外区2019年中考数学二模考试试卷
试卷更新日期:2020-04-01 类型:中考模拟
一、单选题
-
1. 小明观察自己家的冰箱时发现,冷藏室的温度为2℃,冷冻室的温度为﹣20℃,请你帮小明算一算冷藏室的温度比冷冻室的温度高( )A、18℃ B、﹣18℃ C、22℃ D、﹣22℃2. 下列运算正确是( )A、(a+b)2=a2+b2 B、(x2)2=x5 C、(﹣ab)2=a2b2 D、2a+2b=2ab3. 下列图形中,不是中心对称图形的是( )A、
 B、
B、 C、
C、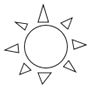 D、
D、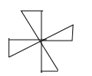 4. 将抛物线y=x2沿着x轴向左平移1个单位,再沿y轴向下平移1个单位,则得到的抛物线解析式为( )A、y=(x﹣1)2﹣1 B、y=(x﹣1)2+1 C、y=(x+1)2+1 D、y=(x+1)2﹣15. 如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是( )
4. 将抛物线y=x2沿着x轴向左平移1个单位,再沿y轴向下平移1个单位,则得到的抛物线解析式为( )A、y=(x﹣1)2﹣1 B、y=(x﹣1)2+1 C、y=(x+1)2+1 D、y=(x+1)2﹣15. 如图,由5个完全相同的小正方体组合成一个立体图形,它的左视图是( )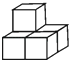 A、
A、 B、
B、 C、
C、 D、
D、 6. 如果反比例函数 的图像经过点(-3,-4),那么该函数的图象位于( )A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第三、四象限7. 如图,AB为⊙O直径,点D为AB延长线上一点,DC为⊙O切线,切点为C,若AC=CD,则AC:BD的值为( )
6. 如果反比例函数 的图像经过点(-3,-4),那么该函数的图象位于( )A、第一、二象限 B、第一、三象限 C、第二、四象限 D、第三、四象限7. 如图,AB为⊙O直径,点D为AB延长线上一点,DC为⊙O切线,切点为C,若AC=CD,则AC:BD的值为( ) A、 B、2 C、 D、8. 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,如果乙队单独完成总工程需多少个月?设乙队单独完成总工程共需 个月,则下列方程正确是( )A、 B、 C、 D、9. 如图,在▱ABCD中,对角线AC与BD相交于点O,且AB⊥AC.若AD=5,AB=3,则对角线BD的长为( )
A、 B、2 C、 D、8. 两个工程队共同参与一项筑路工程,甲队单独施工1个月完成总工程的 ,这时增加了乙队,两队又共同工作了半个月,总工程全部完成,如果乙队单独完成总工程需多少个月?设乙队单独完成总工程共需 个月,则下列方程正确是( )A、 B、 C、 D、9. 如图,在▱ABCD中,对角线AC与BD相交于点O,且AB⊥AC.若AD=5,AB=3,则对角线BD的长为( ) A、 B、2 C、9 D、810. 甲乙二人走步晨练,两人同时同地向距离600米的目标出发,二人所走的路程y(米)与所走的时间t(分)之间的函数关系如图所示,下列说法:①甲走全程的平均速度为75米/分:②第4分钟时,二人在途中相遇;③第2分钟时甲在乙前面100米处;④乙比甲提前2.5分钟到达终点;其中正确有( )个.
A、 B、2 C、9 D、810. 甲乙二人走步晨练,两人同时同地向距离600米的目标出发,二人所走的路程y(米)与所走的时间t(分)之间的函数关系如图所示,下列说法:①甲走全程的平均速度为75米/分:②第4分钟时,二人在途中相遇;③第2分钟时甲在乙前面100米处;④乙比甲提前2.5分钟到达终点;其中正确有( )个. A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 将数201900000用科学记数法表示为 .12. 函数y= 中,自变量x的取值范围是 .13. 把多项式x3﹣2x2+x因式分解的结果是 .14. 不等式组 所有整数解的和为 .15. 计算 的结果是 .16. 如图,AB为⊙O的直径,CD为⊙O的弦,连接AC、AD,若∠BAC=27°,则∠ADC的度数为度.
 17. 若扇形的弧长为6πcm,面积为15πcm2 , 则这个扇形所对的圆心角的度数为 .18. 2018﹣2019中国篮球职业联赛(CBM)季后赛,北京队与上海队争夺一个八强名额,假设比赛采取3场2胜制(即在比赛中先胜2场者晋级八强),则北京队2:0战胜上海队的概率为 .19. 在等边△ABC中,点D为BC边上一点,沿AD将△ABD翻折至△AED,使点B落在点E处,连接CE,若∠CDE=20⁰则∠CED的度数为 .20. 如图,在四边形ABCD中,AC=AD,∠ADB=∠ACB=30°,BD=5,BC=3,则AB的长为 .
17. 若扇形的弧长为6πcm,面积为15πcm2 , 则这个扇形所对的圆心角的度数为 .18. 2018﹣2019中国篮球职业联赛(CBM)季后赛,北京队与上海队争夺一个八强名额,假设比赛采取3场2胜制(即在比赛中先胜2场者晋级八强),则北京队2:0战胜上海队的概率为 .19. 在等边△ABC中,点D为BC边上一点,沿AD将△ABD翻折至△AED,使点B落在点E处,连接CE,若∠CDE=20⁰则∠CED的度数为 .20. 如图,在四边形ABCD中,AC=AD,∠ADB=∠ACB=30°,BD=5,BC=3,则AB的长为 .
三、解答题
-
21. 先化简,再求代数式 的值,其中x=tan60°﹣2sin30°22. 如图,在大小为8×8的正方形方格中,线段AB的两端点都在单位小正方形的顶点上.
 (1)、将线段AB绕点A顺时针旋转90°,使得点B落在点C处,画出△ABC,顶点C在方格的小正方形的顶点上.(2)、在方格中画出以线段AB为一边的菱形ABDE,使其面积为15面积单位,顶点D、E在方格的小正方形顶点上;连接CE和CD,△CDE的面积为面积单位.23. 某中学团委为了解本校学生的课余活动情况,采取随机抽样的方法从阅读、运动、娱乐、其它四个方面调查了若干名学生的课余活动情况每名学生必选且只选一项,并将调查的结果绘制了两幅不完整的统计图,请根据图中提供的信息解答下列问题.
(1)、将线段AB绕点A顺时针旋转90°,使得点B落在点C处,画出△ABC,顶点C在方格的小正方形的顶点上.(2)、在方格中画出以线段AB为一边的菱形ABDE,使其面积为15面积单位,顶点D、E在方格的小正方形顶点上;连接CE和CD,△CDE的面积为面积单位.23. 某中学团委为了解本校学生的课余活动情况,采取随机抽样的方法从阅读、运动、娱乐、其它四个方面调查了若干名学生的课余活动情况每名学生必选且只选一项,并将调查的结果绘制了两幅不完整的统计图,请根据图中提供的信息解答下列问题. (1)、在这次随机抽样中,一共调查了名学生;(2)、通过计算补全条形统计图 , 扇形统计图中阅读部分的扇形圆心角的度数为;(3)、若该校共有800名学生,请你估计该中学在课余时间参与阅读的学生一共有多少名?24. 已知,将矩形ABCD折叠,使点C与点A重合,点D落在点G处,折痕为EF.
(1)、在这次随机抽样中,一共调查了名学生;(2)、通过计算补全条形统计图 , 扇形统计图中阅读部分的扇形圆心角的度数为;(3)、若该校共有800名学生,请你估计该中学在课余时间参与阅读的学生一共有多少名?24. 已知,将矩形ABCD折叠,使点C与点A重合,点D落在点G处,折痕为EF. (1)、如图1,求证:BE=GF;(2)、如图2,连接CF、DG,若CE=2BE,在不添加任何辅助线的情况下,请直接写出图2中的四个三角形,使写出的每个三角形都为等腰三角形25. 某学校艺术节计划为学生购买A、B两种奖品,已知购买40件A种奖品和购买60件B种奖品共需2600元,购买35件A种奖品和购买70件B种奖品共需2800元.(1)、求A、B两种奖品的单价各为多少元?(2)、若学校购买A、B两种奖品共100件,且购买这批奖品的总费用不超过2800元,求最多购买B奖品多少件?26. 已知:AB为⊙O直径,弦CD⊥AB,垂足为H,点E为⊙O上一点, ,BE与CD交于点F.
(1)、如图1,求证:BE=GF;(2)、如图2,连接CF、DG,若CE=2BE,在不添加任何辅助线的情况下,请直接写出图2中的四个三角形,使写出的每个三角形都为等腰三角形25. 某学校艺术节计划为学生购买A、B两种奖品,已知购买40件A种奖品和购买60件B种奖品共需2600元,购买35件A种奖品和购买70件B种奖品共需2800元.(1)、求A、B两种奖品的单价各为多少元?(2)、若学校购买A、B两种奖品共100件,且购买这批奖品的总费用不超过2800元,求最多购买B奖品多少件?26. 已知:AB为⊙O直径,弦CD⊥AB,垂足为H,点E为⊙O上一点, ,BE与CD交于点F. (1)、如图1,求证:BH=FH;(2)、如图2,过点F作FG⊥BE,分别交AC、AB于点G、N,连接EG,求证:EB=EG;(3)、如图3,在(2)的条件下,延长EG交⊙O于M,连接CM、BG,若ON=1,△CMG的面积为6,求线段BG的长.27. 在平面直角坐标系中,点O为坐标原点,过点O的抛物线y=ax2﹣7ax与x轴正半轴交于点A,点D为第三象限抛物线上一点,AD交y轴于点B,OA=2OB,点D纵坐标为﹣4.
(1)、如图1,求证:BH=FH;(2)、如图2,过点F作FG⊥BE,分别交AC、AB于点G、N,连接EG,求证:EB=EG;(3)、如图3,在(2)的条件下,延长EG交⊙O于M,连接CM、BG,若ON=1,△CMG的面积为6,求线段BG的长.27. 在平面直角坐标系中,点O为坐标原点,过点O的抛物线y=ax2﹣7ax与x轴正半轴交于点A,点D为第三象限抛物线上一点,AD交y轴于点B,OA=2OB,点D纵坐标为﹣4. (1)、如图1,求抛物线的解析式;(2)、如图2,点P为第一象限抛物线上一点,过点P作PE⊥x轴,垂足为E,PD交y轴于点C,连接CE,求证:CE∥AD;(3)、如图3,在(2)的条件下,将线段EC绕点E顺时针旋转90°,使点C恰好落在抛物线的点F处,连接OP,点Q为线段OP上一点,若∠FQC=135°,求点Q坐标.
(1)、如图1,求抛物线的解析式;(2)、如图2,点P为第一象限抛物线上一点,过点P作PE⊥x轴,垂足为E,PD交y轴于点C,连接CE,求证:CE∥AD;(3)、如图3,在(2)的条件下,将线段EC绕点E顺时针旋转90°,使点C恰好落在抛物线的点F处,连接OP,点Q为线段OP上一点,若∠FQC=135°,求点Q坐标.