备考2020年中考数学二轮复习拔高训练卷 专题7 四边形
试卷更新日期：2020-04-01 类型：二轮复习
一、单选题
-
1. 一个凸多边形的内角和比它的外角和的 3 倍还多 180°，则这个多边形是（ ）A、九边形 B、八边形 C、七边形 D、六边形2. 下列命题中，真命题是（ ）A、对角线相等的四边形是矩形 B、对角线互相垂直的四边形是菱形 C、对角线互相平分的四边形不一定是平行四边形 D、对角线互相垂直平分且相等的四边形一定是正方形3. 如图，平行四边形ABCD中，E为AD的中点，已知△DEF的面积为S，则四边形ABCE的面积为（ ）
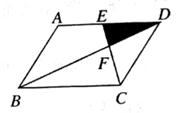A、11S B、10S C、9S D、8S4. 如图，E是平行四边形ABCD的边BA延长线上的一点，CE交AD于点F，下列各式中不正确的是（ ）
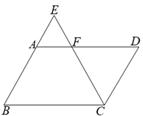A、 B、 C、 D、5. 如图，在平行四边形ABCD和平行四边形BEFG中，AB=AD，BG=BE，点A， B， E在同一直线上，P是线段DF的中点，连接PG、PC，若∠ABC=∠BEF=60°，则 =（ ）
A、 B、 C、 D、6. 如图，在矩形ABCD中，AB=2，BC=3，点E、F、G、H分别在矩形ABCD的各边上，EF∥AC∥HG，EH∥BD∥FG，则四边形EFGH的周长是（ ）
A、 B、13 C、 D、7. 如图，四边形ABCD中，AC=BD，顺次连结四边形各边中点得到的图形是（ ）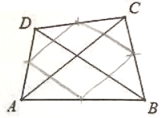
A、菱形 B、矩形 C、正方形 D、以上都不对8. 边长为5的菱形ABCD按如图所示放置在数轴上，其中A点表示数﹣2，C点表示数6，则BD=（ ）
A、4 B、6 C、8 D、109. 如图，在菱形ABCD中，对角线AC与BD相交于点O，OE⊥AB，垂足为E，若∠ADC=130°，则∠AOE的大小为（ ）
A、75° B、65° C、55° D、50°10. 如图，菱形ABCD的周长为40cm，对角线AC，BD相交于点O，DE⊥AB，垂足为E，DE：AB=4：5，则下列结论：①DE=8cm；②BE=4cm；③BD=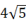
cm；④AC= 
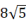cm；⑤S菱形ABCD=80cm，正确的有（ ） 
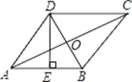A、①②④⑤ B、①②③④ C、①③④⑤ D、①②③⑤11. 如图，四边形ABCD是正方形，直线L1、L2、L3 ， 若L1与L2的距离为5，L2与L3的距离7，则正方形ABCD的面积等于（ ）
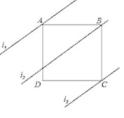A、70 B、74 C、144 D、14812. 如图，正方形ABCD中，M为BC上一点，ME⊥AM，ME交CD于点F，交AD的延长线于点E，若AB＝4，BM＝2，则△DEF的面积为（ ）
A、9 B、8 C、15 D、14.513. 如图，大正方形与小正方形的面积之差是60，则阴影部分的面积是（ ）
A、30 B、20 C、60 D、4014. 如图，在正方形ABCD中，点E是BC延长线上的一点，且AC＝EC，连接AE，交CD于点F，若AB＝1，则线段DF的长是（ ）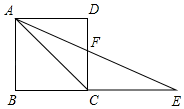
A、 B、 C、2﹣ D、 ﹣115. 如图，已知正方形ABCD的边长为4，点E、F分别在边AB、BC上，且AE=BF=1，CE、DF交于点O.下列结论：①∠DOC=90°， ②OC=OE， ③tan∠OCD = ，④ 中，正确的有（ ）
A、1个 B、2个 C、3个 D、4个二、填空题
-
16. 小明在用计算器计算一个多边形的内角和时，得出的结果为2005°，小芳立即判断他的结果是错误的，小明仔细地复算了一遍，果然发现自己把一个角的度数输入了两遍．你认为正确的内角和应该是°.
17. ▱ABCD中对角线AC和BD交于点O，AC=12，BD=10，AB=m，则m取值范围是.18. 如图，在矩形ABCD中，AB=4，AD=8，将矩形ABCD折叠使点D和点B重合，折痕为EF，则DE=.
19. 如图，正方形ABCD的边长为4，∠DAC的平分线交DC于点E，若点P，Q分别是AD和AE上的动点，则DQ＋PQ的最小值是.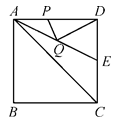
20. 如图，10个边长为1的正方形摆放在平面直角坐标系中，经过A(1，0)点的一条直线，将这10个正方形分成面积相等的两部分，则该直线的解析式为。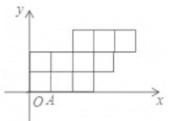
三、解答题
-
21. 如图，矩形ABCD中，E是AD的中点，将△ABE沿BE折叠得到△GBE，且点G在矩形ABCD内部．将BG延长交DC于点F，若DC=nDF，则 为？
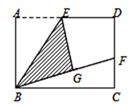22. 如图，点E，F分别为正方形ABCD边AB和CD上的中点， BE与AF交于点G.求证：AD2＝DG·DE
23. 如图，边长为1的正方形OABC绕着点O逆时针旋转30°得到正方形ODEF，连接AF，求 的周长.
24. 如图，已知四边形ABCD为正方形，AB=2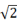
，点E为对角线AC上一动点，连接DE，过点E作EF⊥DE．交射线BC于点F，以DE、EF为邻边作矩形DEFG，连接CG． ①求证：矩形DEFG是正方形；
②探究：CE+CG的值是否为定值？若是，请求出这个定值；若不是，请说明理由．
25. 如图，在矩形ABCD中，AB=18，AD=12，点M是边AB的中点，连结DM，DM与AC交于点G。点E，F分别是CD与DG上的点，连结EF。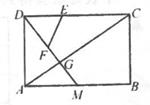
(1)、求证：CG=2AG；(2)、若DE=6，当以E，F，D为顶点的三角形与△CDG相似时，求EF的长；(3)、若点E从点D出发，以每秒2个单位的速度向点C运动，点F从点G出发，以每秒1个单位的速度向点D运动。当一个点到达，另一个随即停止运动。在整个运动过程中，求四边形CEFG的面积的最小值。