浙江省绍兴市2019-2020学年九年级下学期数学教学质量检测（一）
试卷更新日期：2020-04-01 类型：中考模拟
一、选择题（本大题有10小题，每小题4分，共40分.）
-
1. 若小王沿坡度i=3：4的斜坡向上行走10m，则他所在的位置比原来的位置升高了（ ）A、3m B、4m C、6m D、8m2. 如图①是由大小相同的小正方体搭成的几何体，将上层的小正方体平移后得到图②.关于平移前后几何体的三视图，下列说法正确的是（ ）
A、主视图相同 B、左视图相同 C、俯视图相同 D、三种视图均不同3. 按如图所示的运算程序，能使输出的y值为 的是（ ）
A、α=60°，β=45° B、α=30°，β=45° C、α=30°，β=30° D、α=45°，β=30°4. 如图，AB为 O的切线，切点为A.连结AO，BO，BO与 O交于点C，延长BO与 O交于点D，连结AD.若∠ABO=36°，则∠ADC的度数为（ ）
A、27° B、32° C、36° D、54°5. 如图，已知 O的半径为5，直线EF经过 O上一点P（点E，F在点P的两旁），下列条件能判定直线EF与 O相切的是（ ）
A、OP=5 B、OE=OF C、点O到直线EF的距离是4 D、OP⊥EF6. 如图，直线PA、PB、MN分别与 O相切于点A，B，D，PA=PB=8cm，则△PMN的周长为（ ）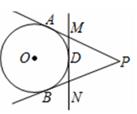
A、8cm B、 cm C、16cm D、 cm7. 如图，O为圆锥的顶点，M为圆锥底面上一点，点P在OM上，一只蜗牛从点P出发，绕圆锥侧面沿最短路线爬行一圈回到点P，若沿OM将圆锥侧面剪开并展开，则所得的侧面展开图是（ ）
A、
B、
C、
D、
8. 如图，AB是 O的直径，DB、DE分别切 O于点B、C，若∠ACE=20°，则∠D的度数是（ ）
A、40° B、50° C、60° D、70°9. 如图，一块矩形木板ABCD斜靠在墙边（OC⊥OB，点A，B，C，D，O在同一平面内），已知AB=a，AD=b，∠BCO=x，则点A到OC的距离等于（ ）
A、asinx+bsinx B、acosx+bsinx C、asinx+bcosx D、acosx+bcosx10. 如图，有一内部装有水的直圆柱形水桶，桶高20dm；另有一直圆柱形的实心铁柱，柱高30dm，直立放置于水桶底面上，水桶内的水面高度为12dm，且水桶与铁柱的底面半径比为2：1.今小贤将铁柱移至水桶外部，过程中水桶内的水量未改变，若不计水桶厚度，则水桶内的水面高度变为（ ）
A、4.5dm B、6dm C、8dm D、9dm二、填空题（本大题有6小题，每小题5分，共30分）
-
11. 如图，在△ABC中，sinB= ，tanC= ，AB=3，则AC的长为 .
12. 如图，∠MAN=60°，若△ABC的顶点B在射线AM上，且AB=2，点C在射线AN上运动，当△ABC是锐角三角形时，BC的取值范围是.
13. 已知等边三角形ABC的边长为3，则它的内切圆半径为.14. 如图所示，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，若以点C为圆心，r为半径的圆与边AB所在直线有公共点，则r的取值范围为.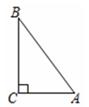
15. 如图是由6个形状、大小完全相同的菱形组成的网格，菱形的顶点称为格点.已知菱形的一个角（∠O）为60°，点A，B，C都在格点上，则sin∠ABC的值是..
16. 已知直线m与半径为10cm的 O相切于点P，AB是 O的一条弦，且 = ，若AB=12cm，则直线m与弦AB之间的距离为.三、解答题（本大题有8小题，第17~20小题每小题8分，第21小题10分，第22、23小题每小题12分，第24小题14分，共80分.）
-
17. 计算：-3sin60°-cos30°+2tan45°．
18. 如图，在离铁塔150m的A处，用测倾仪测得塔顶的仰角为30°12'，测倾仪高AD为1.52m.求铁塔的高BC.（精确到0.1m）（参考数据：sin30°12'≈0.5030，cos30°12'≈0.8643，tan30°12'≈0.5820）
19. 如图，在正方形网格图中建立平面直角坐标系，一条圆弧经过格点A（0，4）、B（-4，4）、C（-6，2），若该圆弧所在圆的圆心为D点，请你利用网格图回答下列问题：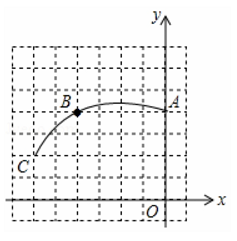
(1)、圆心D的坐标为；(2)、若扇形ADC是一个圆锥的侧面展开图，求该圆锥底面圆的半径长（结果保留根号）.20. 如图，在10×6的正方形网格中，每个小正方形的边长均为1，线段AB、线段EF的端点均在小正方形的顶点上.
①在图中以AB为边画Rt△ABC，使点C在小正方形的顶点上，且∠BAC=90°，tan∠ACB= ；
②在①的条件下，在图中画以EF为边且面积为3的△DEF，使点D在小正方形的顶点上，且∠CBD=45°，连结CD，直接写出线段CD的长.
21. 如图，在△ABC中，AB=AC，∠BAC=120°，点D在BC边上， D经过点A和点B且与BC边相交于点E.
(1)、求证：AC是 D的切线.(2)、若CE= ，求 D的半径.22. 小明家的门框上装有一把防盗门锁（如图1），其平面结构图如图2所示，锁身可以看成由两条等弧 ， 和矩形ABCD组成的， 的圆心是倒锁按钮点M.已知 的弓形高GH=2cm，AD=8cm，EP=11cm.当锁柄PN绕着点N顺时针旋转至NQ位置时，门锁打开，此时直线PQ与 所在的圆相切，且PQ∥DN，tan∠NQP=2.
(1)、求 所在圆的半径；(2)、求线段AB的长度.（ ≈2.236，结果精确到0.1cm）23. 如图，在△ABC中，BA=BC，以AB为直径的 O分别交AC，BC于点D，E，BC的延长线与 O的切线AF交于点F.
(1)、求证：∠ABC=2∠CAF.(2)、若AC= ，CE：EB=1：4，求CE的长.24. 如图，已知直线l：y=- x+8交x轴于点E，点A为x轴上的一个动点（点A不与点E重合），在直线l上取一点B（点B在x轴上方），使BE=5AE，连结AB，以AB为边在AB的右侧作正方形ABCD，连结OB，以OB为直径作 P.
(1)、当点A在点E左侧时，若点B落在y轴上，则AE的长为 ， 点D的坐标为.(2)、若 P与正方形ABCD的边相切于点B，求点B的坐标；(3)、 P与直线BE的交点为Q，连结CQ，当CQ平分∠BCD时，BE的长为.（直接写出答案）