浙江省温州市龙湾区2020年数学中考二模试卷
试卷更新日期:2020-04-01 类型:中考模拟
一、选择题(共10小题)
-
1. -2019的相反数是( )A、2019 B、-2019 C、 D、2. 如图所示的支架是由两个长方体构成的组合体,则它的俯视图是( )
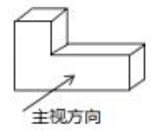 A、
A、 B、
B、 C、
C、 D、
D、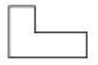 3. 安居物业管理公司对某小区一天的垃圾进行了分类统计,并将统计结果绘制成如图所示的扇形统计图。若某一天产生的垃圾约为300kg,则该小区这一天产生的可回收垃圾约为( )
3. 安居物业管理公司对某小区一天的垃圾进行了分类统计,并将统计结果绘制成如图所示的扇形统计图。若某一天产生的垃圾约为300kg,则该小区这一天产生的可回收垃圾约为( )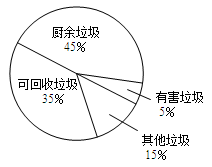 A、15kg B、45kg C、105kg D、135kg4. 一次函数y=2x+4的图象与y轴交点的坐标是( )A、(0,-4) B、(0,4) C、(2,0) D、(-2,0)5. 如图,一个小球沿倾斜角为a的斜坡向下滚动,cosa= .当小球向下滚动了2.5米时,则小球下降的高度是( )
A、15kg B、45kg C、105kg D、135kg4. 一次函数y=2x+4的图象与y轴交点的坐标是( )A、(0,-4) B、(0,4) C、(2,0) D、(-2,0)5. 如图,一个小球沿倾斜角为a的斜坡向下滚动,cosa= .当小球向下滚动了2.5米时,则小球下降的高度是( )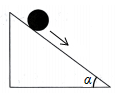 A、2.5米 B、2米 C、1.5米 D、1米6. 若关于x的一元二次方程4x2-4x+c=0有两个相等的实数根,则c的值是( )A、4 B、-4 C、1 D、-17. 如图,在△ABC中,∠ACB=90°,∠B=28°.分别以点A,B为圆心大于 AB的长为半径画弧,两弧交于点D和E,直线DE交AB于点F,连结CF,则∠AFC的度数为( )
A、2.5米 B、2米 C、1.5米 D、1米6. 若关于x的一元二次方程4x2-4x+c=0有两个相等的实数根,则c的值是( )A、4 B、-4 C、1 D、-17. 如图,在△ABC中,∠ACB=90°,∠B=28°.分别以点A,B为圆心大于 AB的长为半径画弧,两弧交于点D和E,直线DE交AB于点F,连结CF,则∠AFC的度数为( ) A、62° B、60° C、58° D、56°8. 有甲、乙两种糖果,原价分别为每千克a元和b元。根据调查,将两种糖果按甲种糖果x千克与乙种糖果y千克的比例混合,取得了较好的销售效果。现在糖果价格有了调整:甲种糖果单价下降15%、乙种糖果单价上涨20%,但按原比例混合的糖果单价恰好不变,则 等于( )A、 B、 C、 D、9. 如图,已知点A,点C在反比例函数y= 上(k>0,x>0)的图象上,AB⊥x轴于点B,连结OC交AB于点D,若CD=2OD,则△BDC与△ADO的面积比为( )
A、62° B、60° C、58° D、56°8. 有甲、乙两种糖果,原价分别为每千克a元和b元。根据调查,将两种糖果按甲种糖果x千克与乙种糖果y千克的比例混合,取得了较好的销售效果。现在糖果价格有了调整:甲种糖果单价下降15%、乙种糖果单价上涨20%,但按原比例混合的糖果单价恰好不变,则 等于( )A、 B、 C、 D、9. 如图,已知点A,点C在反比例函数y= 上(k>0,x>0)的图象上,AB⊥x轴于点B,连结OC交AB于点D,若CD=2OD,则△BDC与△ADO的面积比为( )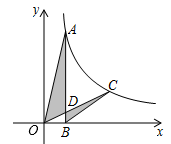 A、 B、 C、 D、10. 如图,一个正六棱柱的表面展开后恰好放入一个矩形内,把其中一部分图形挪动了位置,发现矩形的长留出5cm,宽留出1cm,则该六棱柱的侧面积是( )
A、 B、 C、 D、10. 如图,一个正六棱柱的表面展开后恰好放入一个矩形内,把其中一部分图形挪动了位置,发现矩形的长留出5cm,宽留出1cm,则该六棱柱的侧面积是( )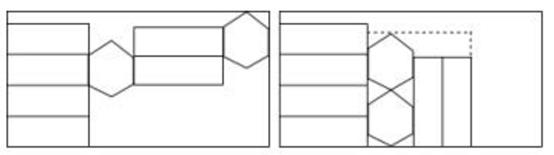 A、(108- )cm2 B、(108- )cm2 C、(54- )cm2 D、(54- )cm2
A、(108- )cm2 B、(108- )cm2 C、(54- )cm2 D、(54- )cm2二、填空题(共6小题)
-
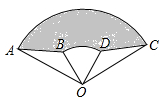
11. 分解因式:m2-8m+16=.12. 小明有5把钥匙,其中有2把钥匙是能打开教室门,则小明任取一把钥匙,恰好能打开教室门的概率是.13. 如果式子 有意义,则x的取值范围是.14. 如图所示,在扇形AOC中,∠AOC=120°,OA=4,以点O为圆心在其同侧画扇形BOD,∠BOD=60°,OB=2,且△AOB≌△COD,则阴影部分的面积是.
 15. 如图,以菱形ABCD的对角线AC为边,在AC的左侧作正方形ACEF、连结FD并延长交EC于点H,若正方形ACEF的面积是菱形ABCD面积的1.4倍,CH=6,则EF=.
15. 如图,以菱形ABCD的对角线AC为边,在AC的左侧作正方形ACEF、连结FD并延长交EC于点H,若正方形ACEF的面积是菱形ABCD面积的1.4倍,CH=6,则EF=.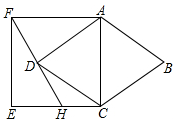 16. 小明家的门框上装有一把防盗门锁(如图1).其平面结构图如图2所示,锁身可以看成由两条等弧
16. 小明家的门框上装有一把防盗门锁(如图1).其平面结构图如图2所示,锁身可以看成由两条等弧 ,
,  和矩形ABCD组成,
和矩形ABCD组成,  的圆心是倒锁按钮点M.其中
的圆心是倒锁按钮点M.其中  的弓高GH=2cm,AD=8cm,EP=11cm.当锁柄PN绕着点N旋转至AQ位置时,门锁打开,此时直线PQ与
的弓高GH=2cm,AD=8cm,EP=11cm.当锁柄PN绕着点N旋转至AQ位置时,门锁打开,此时直线PQ与  所在的圆相切,且PQ∥DN,tan∠NQP=2,则AB的长度约为cm.(结果精确到0.1cm 参考数据: ≈1.732, ≈2.236)
所在的圆相切,且PQ∥DN,tan∠NQP=2,则AB的长度约为cm.(结果精确到0.1cm 参考数据: ≈1.732, ≈2.236) 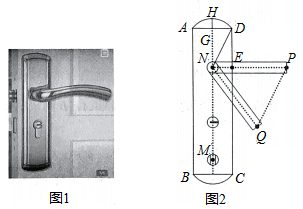
三、解答题(共8小题)
-
17.(1)、计算:(-2)0+|1-5|-( )-1
(2)、化简:(a+1)(a-1)-a(a-2).18. 如图,点D是等边△ABC内一点,将线段AD绕着点A逆时针旋转60°得到线段AE,连结CD并延长交AB于点F,连结BD,CE.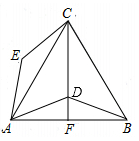 (1)、求证:△ACE≌△ABD(2)、当CF⊥AB时,∠ADB=140°,求∠ECD的度数。19. 如图,这是一张6×6的方格纸,方格纸中的每个小正方形的边长均为1,线段AB的端点均在格点上.请按要求完成下列作图:①仅用无刻度直尺,且不能用直尺中的直角;②保留作图痕迹。
(1)、求证:△ACE≌△ABD(2)、当CF⊥AB时,∠ADB=140°,求∠ECD的度数。19. 如图,这是一张6×6的方格纸,方格纸中的每个小正方形的边长均为1,线段AB的端点均在格点上.请按要求完成下列作图:①仅用无刻度直尺,且不能用直尺中的直角;②保留作图痕迹。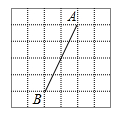 (1)、请以线段AB为斜边作等腰直角△ABC(作出一个即可)。(2)、在(1)的基础上,作出BC边上的中线AD.20. 为让学生感受中华诗词之类,某校九级举行了“诗词大奏”,为了解九年级A,B两班学生的“诗词大赛”成绩,分别从每班50名学生中各随机抽取20人的“诗词大赛”成绩(满分为40分,成绩续均为整数),制成如图所示的统计图。
(1)、请以线段AB为斜边作等腰直角△ABC(作出一个即可)。(2)、在(1)的基础上,作出BC边上的中线AD.20. 为让学生感受中华诗词之类,某校九级举行了“诗词大奏”,为了解九年级A,B两班学生的“诗词大赛”成绩,分别从每班50名学生中各随机抽取20人的“诗词大赛”成绩(满分为40分,成绩续均为整数),制成如图所示的统计图。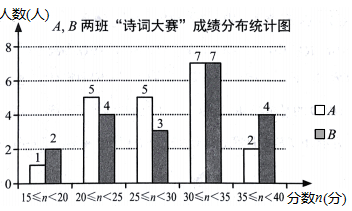 (1)、若将不低于35分的成绩评为优秀,请你估计一下哪个班级优秀人数多?多几人?(2)、请你选择适当的统计量来说到A,B两班哪个班级的整体成绩较好?21. 如图,抛物线M1:y=-x2+4x交x轴正半轴于点A,将抛物线M1平移得到抛物线M2:y=-x2+bx+c,M1与M2交于点B,直线OB交M2于点C,点C的横坐标为6,且OB=BC
(1)、若将不低于35分的成绩评为优秀,请你估计一下哪个班级优秀人数多?多几人?(2)、请你选择适当的统计量来说到A,B两班哪个班级的整体成绩较好?21. 如图,抛物线M1:y=-x2+4x交x轴正半轴于点A,将抛物线M1平移得到抛物线M2:y=-x2+bx+c,M1与M2交于点B,直线OB交M2于点C,点C的横坐标为6,且OB=BC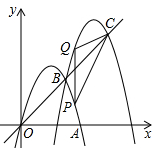 (1)、①直接写出点B,点C的坐标;
(1)、①直接写出点B,点C的坐标;②求抛物线M2的表达式;
(2)、点P是抛物线M1上AB间一点,作PQ⊥x轴交抛物线M2于点Q连结CP,CQ,设点P的横标为m.当m为何值时,使△CPQ的面积最大,并求出最大值。22. 如图1,平面内有一点P到△ABC的三个顶点的距离分别为PA,PB,PC.若满足PA2=PB2+PC2 , 则称点P为△ABC关于点A的勾股点。如图2,E是矩形ABCD内一点,且点C是△ABE关于点A的勾股点,连接DE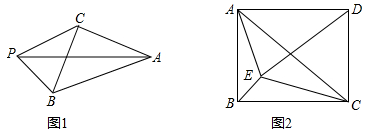 (1)、求证:CE=CD.(2)、若AB=5,BC=6,DA=DE,求AE的长。23. 某礼品店从文化用品市场批发甲、乙、丙三种礼品(每种礼品都有),各礼品的数量和批发单价列表如下:
(1)、求证:CE=CD.(2)、若AB=5,BC=6,DA=DE,求AE的长。23. 某礼品店从文化用品市场批发甲、乙、丙三种礼品(每种礼品都有),各礼品的数量和批发单价列表如下:甲
乙
丙
数量(个)
m
3m
n
批发单价(元)
a(1≤m≤10)
b
10
0.8a(m>10)
(1)、当m=5时,若这三种礼器共批发35个,甲礼品的总价不低于丙礼品的总价,求a的最小值;(2)、已知该店用1320元批发了这三种礼品,且a=5b:①当m=25时,若批发这三种礼品的平均单价为11元/个,求b的值;
②当7<m<20时,若该店批发了20个丙礼品,且a为正整数,求a的值。
24. 如图,在Rt△ABC中,∠ABC=90°,⊙O(圆心O在△ABC内部)经过B,C两点,交线段AC于点D,直径BH交AC于点E,点A关于直线BD的对称点F落在 ⊙O上.连结BF.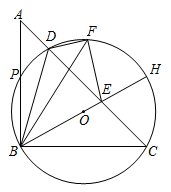 (1)、求证:∠C=45°:(2)、在圆心O的运动过程中;
(1)、求证:∠C=45°:(2)、在圆心O的运动过程中;①若 tan∠EDF= ,AB=6,求CE的长;
②若点F关于AC的对称点落在△BFE边上时,求点 的值。(直接写出答案);
(3)、令 ⊙O与边AB的另一个交点为P,连结PC,交BD于点Q,若PC⊥BF,垂足为点G,求证:BD=AD+CE