浙江省台州市温岭市2020年数学中考一模试卷

试卷更新日期：2020-04-01 类型：中考模拟

进入出卷网下载

一、选择题（本大题共10小题，共40分）

1. 如果a与﹣3互为相反数，那么a等于（　　）

A、-3 B、3 C、 $- \frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 习近平主席在2018年新年贺词中指出，2017年，基本医疗保险已经覆盖1350000000人．将1350000000用科学记数法表示为（）

A、135×10⁷ B、1.35×10⁹ C、13.5×10⁸ D、1.35×10¹⁴

查看试题解析
3. 下列计算正确的是（）

A、a³+a²＝a⁵ B、a³•a²＝a⁵ C、(2a²)³＝6a⁶ D、a⁶÷a²＝a³

查看试题解析
4.
如图，是某个几何体从不同方向看到的形状图（视图），这个几何体的表面能展开成下面的哪个平面图形？（　　）

A、 B、 C、 D、

查看试题解析
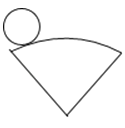5. 如图，数轴A、B上两点分别对应实数a、b，则下列结论正确的是（　　）

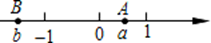A、a+b＞0 B、ab＝0 C、 $\frac{1}{a} - \frac{1}{b} < 0$ D、 $\frac{1}{a} + \frac{1}{b} > 0$

查看试题解析
6. 某车间20名工人每天加工零件数如表所示：

每天加工零件数

4

5

6

7

8

人数

3

6

5

4

2

这些工人每天加工零件数的众数、中位数分别是（）

A、5，5 B、5，6 C、6，6 D、6，5

查看试题解析
7. 如图，点A，B，P是⊙O上的三点，若∠AOB＝40°，则∠APB的度数为（　　）

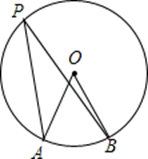A、80° B、140° C、20° D、50°

查看试题解析
8. 如图，在▱ABCD中，用直尺和圆规作∠BAD的平分线AG交BC于点E，若BF＝6，AB＝4，则AE的长为（　　）

A、 $\sqrt{7}$ B、 $2 \sqrt{7}$ C、 $3 \sqrt{7}$ D、 $4 \sqrt{7}$

查看试题解析
9. 我们知道：四边形具有不稳定性．如图，在平面直角坐标系中，矩形ABCD的边AB在x轴上，其中O点是坐标原点，AO＝2，BO＝3，BC＝4，点A、B是固定点，把正方形沿箭头方向推，使点D落在y轴正半轴上点D′处，则点C的对应点C′的坐标为（　　）

A、 $(2 \sqrt{3} ， 3)$ B、 $(2 \sqrt{3} ， 5)$ C、 $(3 ， 2 \sqrt{3})$ D、 $(5 ， 2 \sqrt{3})$

查看试题解析
10. 如图1，动点K从△ABC的顶点A出发，沿AB﹣BC匀速运动到点C停止，在动点K运动过程中，线段AK的长度y与运动时间x的函数关系如图2所示，其中点D为曲线部分的最低点，若△ABC的面积是10 $\sqrt{6}$ 则a＝（　　）

A、7 B、 $3 \sqrt{6}$ C、8 D、 $4 \sqrt{6}$

查看试题解析

二、填空题（本大题共 6 小题，共 30 分）

11. 分解因式：x²﹣4x＝

查看试题解析
12. 若a，b都是实数， $b = \sqrt{1 - 2 a} + \sqrt{2 a - 1} - 2$ ，则a^b的值为.

查看试题解析
13. 如图，已知点E为矩形ABCD内的点，若EB＝EC，则EAED（填“＞”、“＜”或“＝”）

查看试题解析
14. 如果抛物线y＝（x﹣m）²+m+1的对称轴是直线x＝1，那么它的顶点坐标那么它的顶点坐标为

查看试题解析
15. 如果点（-1，y₁）、B（1，y₂）、C（2，y₃）是反比例函数y= $\frac{1}{x}$ 图象上的三个点，则y₁、y₂、y₃的大小关系是．

查看试题解析
16. 如图，在直径为8的弓形ACB中，弦AB＝4 $\sqrt{3}$ ，C是弧AB的中点，点M为弧上动点，CN⊥AM于点N，当点M从点B出发逆时针运动到点C，点N所经过的路径长为.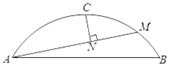

查看试题解析

三、解答题（本大题共 8 小题，共 80 分）

17. $| - 1 + \sqrt{2} | - \frac{1}{2} \sqrt{8} - {(5 - π)}^{0} + 4 cos 45^{\circ}$

查看试题解析
18. 附加题：（y﹣z）²+（x﹣y）²+（z﹣x）²=（y+z﹣2x）²+（z+x﹣2y）²+（x+y﹣2z）² ．求 $\frac{(y z + 1) (z x + 1) (x y + 1)}{(x^{2} + 1) (y^{2} + 1) (z^{2} + 1)}$ 的值．

查看试题解析
19. 我市某中学艺术节期间，向全校学生征集书画作品，九年级美术王老师从全年级14个班中随机抽取了4个班，对征集到的作品的数量进行了分析统计，制作了如图两幅不完整的统计图．

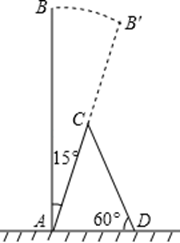
(1)、王老师采取的调查方式是（填“普查”或“抽样调查”），请把图2补充完整；

(2)、王老师所调查的四个班平均每个班征集作品多少件？请估计全年级共征集到作品多少件？

(3)、如果全年级参展作品中有5件获得一等奖，其中有3名作者是男生，2名作者是女生，现在要在其中抽两人去参见学校总结表彰座谈会，求恰好抽中一男一女的概率要求写出用树状图或列表分析过程）

查看试题解析
20. 每年的6至8月份是台风多发季节，某次台风来袭时，一棵大树树干AB（假定树干AB垂直于地面）被刮倾斜15°后折断倒在地上，树的项部恰好接触到地面D（如图所示），量得树干的倾斜角为∠BAC＝15°，大树被折断部分和地面所成的角∠ADC＝60°，AD＝4米，求这棵大树AB原来的高度是多少米？（结果精确
到个位，参考数据： $\sqrt{2} \approx 1.4 ， \sqrt{3} \approx 1.7 ， \sqrt{6} \approx 2.4$ ）

查看试题解析
21. 如图，点C在以AB为直径的⊙O上，AD与过点C的切线垂直，垂足为点D，AD交⊙O于点E

(1)、

求证：AC平分∠DAB；

(2)、连接BE交AC于点F，若AB＝10，AC＝8，求EF的长．

查看试题解析
22. 某公司销售一种新型节能产品，现准备从国内和国外两种销售方案中选择一种进行销售．
若只在国内销售，销售价格y（元/件）与月销量x（件）的函数关系式为y＝ $- \frac{1}{100}$ x+150，成本为20元/件，无论销售多少，每月还需支出广告费62500元，设月利润为w_内（元）（利润＝销售额﹣成本﹣广告费）．
若只在国外销售，销售价格为150元/件，受各种不确定因素影响，成本为a元/件（a为常数，10≤a≤40），当月销量为x（件）时，每月还需缴纳 $\frac{1}{100}$ x²元的附加费，设月利润为w_外（元）（利润＝销售额﹣成本﹣附加费）

(1)、当x＝1000时，y＝元/件，w_内＝元；

(2)、分别求出w_内， w_外与x间的函数关系式（不必写x的取值范围）；

(3)、当x为何值时，在国内销售的月利润最大？若在国外销售月利润的最大值与在国内销售月利润的最大值相同，求a的值；

查看试题解析
23. 问题发现．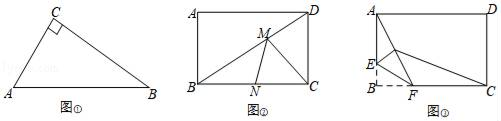

(1)、如图①，Rt△ABC中，∠C＝90°，AC＝3，BC＝4，点D是AB边上任意一点，则CD的最小值为．

(2)、如图②，矩形ABCD中，AB＝3，BC＝4，点M、点N分别在BD、BC上，求CM+MN的最小值．

(3)、如图③，矩形ABCD中，AB＝3，BC＝4，点E是AB边上一点，且AE＝2，点F是BC边上的任意一点，把△BEF沿EF翻折，点B的对应点为G，连接AG、CG，四边形AGCD的面积是否存在最小值，若存在，求这个最小值及此时BF的长度．若不存在，请说明理由．

查看试题解析
24.
如图1，在平面直角坐标系中，一次函数y＝﹣2x+8的图象与x轴，y轴分别交于点A，点C，过点A作AB⊥x轴，垂足为点A，过点C作CB⊥y轴，垂足为点C，两条垂线相交于点B．

(1)、线段AB、BC、AC的长分别为AB ， BC= ， AC；

(2)、折叠图1中的△ABC，使点A与点C重合，再将折叠后的图形展开，折痕DE交AB于点D，交AC于点E，连接CD，如图2．
请从下列A、B两题中任选一题作答，我选择（）题．
A：①求线段AD的长；
②在y轴上，是否存在点P，使得△APD为等腰三角形？若存在，请直接写出符合条件的所有点P的坐标；若不存在，请说明理由．
B：①求线段DE的长；
②在坐标平面内，是否存在点P（除点B外），使得以点A，P，C为顶点的三角形与△ABC全等？若存在，请直接写出所有符合条件的点P的坐标；若不存在，请说明理由．

查看试题解析

每天加工零件数	4	5	6	7	8
人数	3	6	5	4	2