江苏省南通市2020年数学中考模拟试卷(三)
试卷更新日期:2020-04-01 类型:中考模拟
一、单选题
-
1. 下列图形中,是中心对称图形,但不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列运算正确的是( )A、 B、 C、 D、3. 有31位学生参加学校举行的“最强大脑”智力游戏比赛,比赛结束后根据每个学生的最后得分计算出中位数、平均数、众数和方差,如果去掉一个最高分和一个最低分,则一定不发生变化的是( )A、中位数 B、平均数 C、众数 D、方差4. 式子 有意义的x的取值范围是( )A、 且x≠1 B、x≠1 C、 D、 且x≠15. 点A(x1 , y1)、B(x2 , y2)都在直线y=kx+2(k<0)上,且x1<x2则y1、y2的大小关系是( )A、y1 =y2 B、y1 <y2 C、y1 >y2 D、y1 ≥y26. 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,AC=8,BC=6,则∠ACD的正切值是( )
2. 下列运算正确的是( )A、 B、 C、 D、3. 有31位学生参加学校举行的“最强大脑”智力游戏比赛,比赛结束后根据每个学生的最后得分计算出中位数、平均数、众数和方差,如果去掉一个最高分和一个最低分,则一定不发生变化的是( )A、中位数 B、平均数 C、众数 D、方差4. 式子 有意义的x的取值范围是( )A、 且x≠1 B、x≠1 C、 D、 且x≠15. 点A(x1 , y1)、B(x2 , y2)都在直线y=kx+2(k<0)上,且x1<x2则y1、y2的大小关系是( )A、y1 =y2 B、y1 <y2 C、y1 >y2 D、y1 ≥y26. 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的中线,AC=8,BC=6,则∠ACD的正切值是( )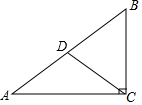 A、 B、 C、 D、7. 如图,在⊙O中,点A、B、C在⊙O上,且∠ACB=110°,则∠α=( )
A、 B、 C、 D、7. 如图,在⊙O中,点A、B、C在⊙O上,且∠ACB=110°,则∠α=( )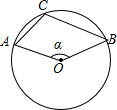 A、70° B、110° C、120° D、140°8. 如图,平行四边形ABCD中,对角线AC,BD相交于点O,点E是CD的中点,则△ODE与△AOB的面积比为( )
A、70° B、110° C、120° D、140°8. 如图,平行四边形ABCD中,对角线AC,BD相交于点O,点E是CD的中点,则△ODE与△AOB的面积比为( )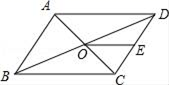 A、1:2 B、1:3 C、1:4 D、1:59. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )
A、1:2 B、1:3 C、1:4 D、1:59. 已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是( )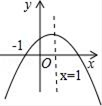 A、abc>0 B、b2﹣4ac<0 C、9a+3b+c>0 D、c+8a<010.
A、abc>0 B、b2﹣4ac<0 C、9a+3b+c>0 D、c+8a<010.如图,矩形ABCD中,AB=3,BC=4,动点P从A点出发,按A→B→C的方向在AB和BC上移动,记PA=x,点D到直线PA的距离为y,则y关于x的函数图象大致是( )
 A、
A、 B、
B、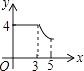 C、
C、 D、
D、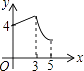
二、填空题
-
11. 舌尖上的浪费让人触目惊心,据统计中国每年浪费的食物总量折合粮食约499.5亿千克,这个数用科学记数法应表示为 .12. 因式分解:3a3﹣6a2b+3ab2= .13. 已知 、 在同一个反比例函数图象上,则 .14. 分式方程 + =1的解为.15. 如图,等边 的边长为2,则点B的坐标为.
 16. 《九章算术》是中国传统数学名著,其中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两问牛,羊各直金几何?”译文:“假设有5头牛,2只羊,值金10两;2头牛,5只羊,值金8两.问每头牛、每只羊各值金多少两?”若设每头牛、每只羊分别值金 两、 两,根据题意,则可列方程组为17. 如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为 .
16. 《九章算术》是中国传统数学名著,其中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两问牛,羊各直金几何?”译文:“假设有5头牛,2只羊,值金10两;2头牛,5只羊,值金8两.问每头牛、每只羊各值金多少两?”若设每头牛、每只羊分别值金 两、 两,根据题意,则可列方程组为17. 如图,在矩形ABCD中,AB=4,BC=6,E是矩形内部的一个动点,且AE⊥BE,则线段CE的最小值为 .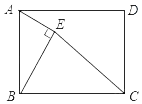 18. 如图,点A在双曲线y= 上,点B在双曲线y= (k≠0)上,AB∥x轴,过点A作AD⊥x轴 于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为 .
18. 如图,点A在双曲线y= 上,点B在双曲线y= (k≠0)上,AB∥x轴,过点A作AD⊥x轴 于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为 .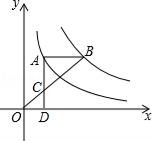
三、解答题
-
19.(1)、先化简,再求值:(2﹣ )÷ ,其中x=2.(2)、计算:| ﹣2|+2010°﹣(﹣ )﹣1+3tan30°.20. 解方程:(1)、x2﹣8x+1=0(2)、(3)、解不等式组: .21.
“端午节”是我国的传统佳节,民间历来有吃“粽子”的习俗.我市某食品厂为了解市民对去年销量较好的肉馅粽、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不同口味粽子的喜爱情况,在节前对某居民区市民进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整).
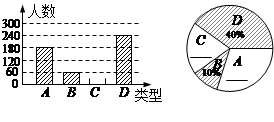
请根据以上信息回答:(1)、本次参加抽样调查的居民有多少人?
(2)、将两幅不完整的图补充完整;
(3)、若居民区有8000人,请估计爱吃D粽的人数;
(4)、若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个.用列表或画树状图的方法,求他第二个吃到的恰好是C粽的概率.
22. 在国家的宏观调控下,某市的商品房成交价由去年10月份的14000元/ 下降到12月份的11340元/ .(1)、求11、12两月份平均每月降价的百分率是多少?(2)、如果房价继续回落,按此降价的百分率,你预测到今年2月份该市的商品房成交均价是否会跌破10000元/ ?请说明理由23. 小亮一家到桃林口水库游玩.在岸边码头 处,小亮和爸爸租船到库区游玩,妈妈在岸边码头 处观看小亮与爸爸在水面划船,小船从 处出发,沿北偏东60°方向划行,划行速度是20米/分钟,划行10分钟后到 处,接着向正南方向划行一段时间到 处,在 处小亮观测到妈妈所在的 处在北偏西37°的方向上,这时小亮与妈妈相距多少米?(精确到 ,参考数据: ) 24. 如图,在等边三角形ABC中,点D,E分别在BC, AB上,且∠ADE=60°.求证:△ADC~△DEB.
24. 如图,在等边三角形ABC中,点D,E分别在BC, AB上,且∠ADE=60°.求证:△ADC~△DEB.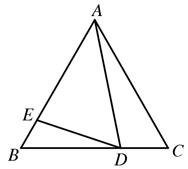 25. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连接AC,过 上一点E作EG∥AC交CD的延长线于点G,连接AE交CD于点F,且EG=FG,连接CE.
25. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连接AC,过 上一点E作EG∥AC交CD的延长线于点G,连接AE交CD于点F,且EG=FG,连接CE.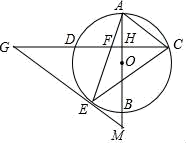 (1)、求证:EG是⊙O的切线;(2)、延长AB交GE的延长线于点M,若AH=3,CH=4,求EM的值.26. 如图,▱ABCD的对角线AC,BD相交于点O.E,F是AC上的两点,并且AE=CF,连接DE,BF.
(1)、求证:EG是⊙O的切线;(2)、延长AB交GE的延长线于点M,若AH=3,CH=4,求EM的值.26. 如图,▱ABCD的对角线AC,BD相交于点O.E,F是AC上的两点,并且AE=CF,连接DE,BF. (1)、求证:△DOE≌△BOF;(2)、若BD=EF,连接DE,BF.判断四边形EBFD的形状,并说明理由.27. 已知点A在x轴负半轴上,点B在y轴正半轴上,线段OB的长是方程x2﹣2x﹣8=0的解,tan∠BAO= .
(1)、求证:△DOE≌△BOF;(2)、若BD=EF,连接DE,BF.判断四边形EBFD的形状,并说明理由.27. 已知点A在x轴负半轴上,点B在y轴正半轴上,线段OB的长是方程x2﹣2x﹣8=0的解,tan∠BAO= .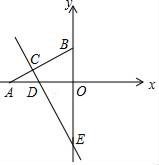 (1)、求点A的坐标;(2)、点E在y轴负半轴上,直线EC⊥AB,交线段AB于点C,交x轴于点D,S△DOE=16.若反比例函数y= 的图象经过点C,求k的值;(3)、在(2)条件下,点M是DO中点,点N,P,Q在直线BD或y轴上,是否存在点P,使四边形MNPQ是矩形?若存在,请直接写出点P的坐标;若不存在,请说明理由.28. 如图①已知抛物线y=ax2﹣3ax﹣4a(a<0)的图象与x轴交于A、B两点(A在B的左侧),与y的正半轴交于点C,连结BC,二次函数的对称轴与x轴的交点为E.
(1)、求点A的坐标;(2)、点E在y轴负半轴上,直线EC⊥AB,交线段AB于点C,交x轴于点D,S△DOE=16.若反比例函数y= 的图象经过点C,求k的值;(3)、在(2)条件下,点M是DO中点,点N,P,Q在直线BD或y轴上,是否存在点P,使四边形MNPQ是矩形?若存在,请直接写出点P的坐标;若不存在,请说明理由.28. 如图①已知抛物线y=ax2﹣3ax﹣4a(a<0)的图象与x轴交于A、B两点(A在B的左侧),与y的正半轴交于点C,连结BC,二次函数的对称轴与x轴的交点为E.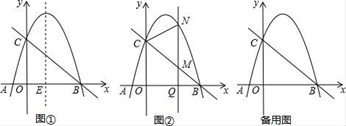 (1)、抛物线的对称轴与x轴的交点E坐标为 , 点A的坐标为;(2)、若以E为圆心的圆与y轴和直线BC都相切,试求出抛物线的解析式;(3)、在(2)的条件下,如图②Q(m,0)是x的正半轴上一点,过点Q作y轴的平行线,与直线BC交于点M,与抛物线交于点N,连结CN,将△CMN沿CN翻折,M的对应点为M′.在图②中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
(1)、抛物线的对称轴与x轴的交点E坐标为 , 点A的坐标为;(2)、若以E为圆心的圆与y轴和直线BC都相切,试求出抛物线的解析式;(3)、在(2)的条件下,如图②Q(m,0)是x的正半轴上一点,过点Q作y轴的平行线,与直线BC交于点M,与抛物线交于点N,连结CN,将△CMN沿CN翻折,M的对应点为M′.在图②中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.