江苏省扬州市宝应县2020年数学中考一模试卷
试卷更新日期:2020-04-01 类型:中考模拟
一、单选题
-
1. 的倒数是( )A、 B、 C、 D、2. 下列各式中,计算正确的是( )A、 B、 C、 D、3. 将一副三角板按如图所示的位置摆放在直尺上,则∠1的度数为( )
 A、60° B、65° C、75° D、85°4. 一个由圆柱和长方体组成的几何体如图水平放置,它的俯视图是( )
A、60° B、65° C、75° D、85°4. 一个由圆柱和长方体组成的几何体如图水平放置,它的俯视图是( ) A、
A、 B、
B、 C、
C、 D、
D、 5. 已知反比例函数 ,在下列结论中,不正确的是( ).A、图象必经过点(1,2); B、 随 的增大而减少; C、图象在第一.三象限 ; D、若 >1,则 <2 .6. 若一元二次方程x2﹣2x+m=0有两个不相同的实数根,则实数m的取值范围是( )A、m≥1 B、m≤1 C、m>1 D、m<17. 十堰即将跨入高铁时代,钢轨铺设任务也将完成.现还有 米的钢轨需要铺设,为确保年底通车,如果实际施工时每天比原计划多铺设 米,就能提前 天完成任务.设原计划每天铺设钢轨 米,则根据题意所列的方程是( )A、 B、 C、 D、8. 如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN等于( )
5. 已知反比例函数 ,在下列结论中,不正确的是( ).A、图象必经过点(1,2); B、 随 的增大而减少; C、图象在第一.三象限 ; D、若 >1,则 <2 .6. 若一元二次方程x2﹣2x+m=0有两个不相同的实数根,则实数m的取值范围是( )A、m≥1 B、m≤1 C、m>1 D、m<17. 十堰即将跨入高铁时代,钢轨铺设任务也将完成.现还有 米的钢轨需要铺设,为确保年底通车,如果实际施工时每天比原计划多铺设 米,就能提前 天完成任务.设原计划每天铺设钢轨 米,则根据题意所列的方程是( )A、 B、 C、 D、8. 如图,在△ABC中,AB=AC=5,BC=6,点M为BC的中点,MN⊥AC于点N,则MN等于( )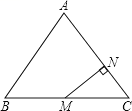 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
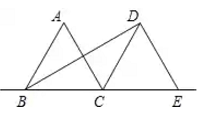
9. 若分式 有意义,则x的取值范围是 。10. 分解因式:2a3﹣8a= .11. 中国“神威·太湖之光”计算机最高运行速度为1250000000亿次/秒,将数1250000000用科学记数法可表示为.12. 如图,△ABC和△DCE都是边长为2的等边三角形,点B、C、E在同一条直线上,连接BD,则BD的长为 .
 13. 某品牌旗舰店平日将某商品按进价提高40%后标价,在某次电商购物节中,为促销该商品,按标价8折销售,售价为2240元,则这种商品的进价是元.14. 如图所示,一次函数 ( 、 为常数,且 )的图象经过点 ,则不等式 的解集为 .
13. 某品牌旗舰店平日将某商品按进价提高40%后标价,在某次电商购物节中,为促销该商品,按标价8折销售,售价为2240元,则这种商品的进价是元.14. 如图所示,一次函数 ( 、 为常数,且 )的图象经过点 ,则不等式 的解集为 .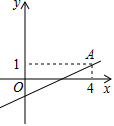 15. 已知不等式组 的解集为 ,则 的取值范围是 .16. 如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,sin∠CAM= ,则tan∠B= .
15. 已知不等式组 的解集为 ,则 的取值范围是 .16. 如图,在Rt△ABC中,∠C=90°,AM是BC边上的中线,sin∠CAM= ,则tan∠B= .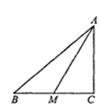 17. 关于 的分式方程 的解为正数,则 的取值范围是.18. 如图,在平面直角坐标中,一次函数y=﹣4x+4的图象与x轴、y轴分别交于A、B两点.正方形ABCD的顶点C、D在第一象限,顶点D在反比例函数 (k≠0)的图象上.若正方形ABCD向左平移n个单位后,顶点C恰好落在反比例函数的图象上,则n的值是.
17. 关于 的分式方程 的解为正数,则 的取值范围是.18. 如图,在平面直角坐标中,一次函数y=﹣4x+4的图象与x轴、y轴分别交于A、B两点.正方形ABCD的顶点C、D在第一象限,顶点D在反比例函数 (k≠0)的图象上.若正方形ABCD向左平移n个单位后,顶点C恰好落在反比例函数的图象上,则n的值是.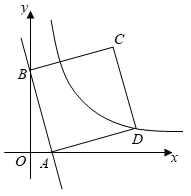
三、解答题
-
19.(1)、计算:|﹣ |+(﹣1)2019+2sin30°+( )0(2)、解方程:20. 先化简,再求值 ,其中 满足
21. 关于x的方程 有实数根,且m为正整数,求m的值及此时方程的根.22. 如图,在四边形ABCD中,AD∥BC,E为CD的中点,连接AE、BE,BE⊥AE,延长AE交BC的延长线于点F.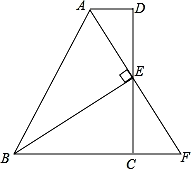
求证:
(1)、FC=AD;(2)、AB=BC+AD.23. 在平面直角坐标系中,一次函数的图象与坐标轴围成的三角形,叫做此一次函数的坐标三角形.例如,图中的一次函数的图象与x,y轴分别交于点A,B,则△OAB为此函数的坐标三角形.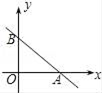 (1)、求函数y= x+3的坐标三角形的三条边长;(2)、若函数y= x+b(b为常数)的坐标三角形周长为16,求此三角形面积.24. 已知电视发射塔BC,为稳固塔身,周围拉有钢丝地锚线(如图线段AB),若AB=60m,并且AB与地面成45°角,欲升高发射塔的高度到CB′,同时原地锚线仍使用,若塔升高后使地锚线与地面成60°角,求电视发射塔升高了多少米?(即BB′的高度)
(1)、求函数y= x+3的坐标三角形的三条边长;(2)、若函数y= x+b(b为常数)的坐标三角形周长为16,求此三角形面积.24. 已知电视发射塔BC,为稳固塔身,周围拉有钢丝地锚线(如图线段AB),若AB=60m,并且AB与地面成45°角,欲升高发射塔的高度到CB′,同时原地锚线仍使用,若塔升高后使地锚线与地面成60°角,求电视发射塔升高了多少米?(即BB′的高度) 25. 如图,帆船A和帆船B在太湖湖面上训练,O为湖面上的一个定点,教练船静候于O点,训练时要求A、B两船始终关于O点对称.以O为原点,建立如图所示的坐标系,x轴、y轴的正方向分别表示正东、正北方向.设A、B两船可近似看成在双曲线y= 上运动,湖面风平浪静,双帆远影优美,训练中当教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).
25. 如图,帆船A和帆船B在太湖湖面上训练,O为湖面上的一个定点,教练船静候于O点,训练时要求A、B两船始终关于O点对称.以O为原点,建立如图所示的坐标系,x轴、y轴的正方向分别表示正东、正北方向.设A、B两船可近似看成在双曲线y= 上运动,湖面风平浪静,双帆远影优美,训练中当教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).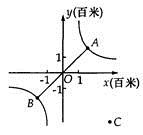 (1)、发现C船时,A、B、C三船所在位置的坐标分别为A( , )、B( , )和C( , );(2)、发现C船,三船立即停止训练,并分别从A、O、B三点出发沿最短路线同时前往救援,设A、B两船的速度相等,教练船与A船的速度之比为3:4,问教练船是否最先赶到?请说明理由.26. 一种火爆的网红电子产品,每件产品成本 元、工厂将该产品进行网络批发,批发单价 (元)与一次性批发量 (件)( 为正整数)之间满足如图所示的函数关系.
(1)、发现C船时,A、B、C三船所在位置的坐标分别为A( , )、B( , )和C( , );(2)、发现C船,三船立即停止训练,并分别从A、O、B三点出发沿最短路线同时前往救援,设A、B两船的速度相等,教练船与A船的速度之比为3:4,问教练船是否最先赶到?请说明理由.26. 一种火爆的网红电子产品,每件产品成本 元、工厂将该产品进行网络批发,批发单价 (元)与一次性批发量 (件)( 为正整数)之间满足如图所示的函数关系.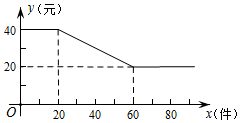 (1)、直接写出 与 之间所满足的函数关系式,并写出自变量 的取值范围;(2)、若一次性批发量不超过 件,当批发量为多少件时,工厂获利最大?最大利润是多少?27. 数学课上,李老师出示范了如下框中的题目.
(1)、直接写出 与 之间所满足的函数关系式,并写出自变量 的取值范围;(2)、若一次性批发量不超过 件,当批发量为多少件时,工厂获利最大?最大利润是多少?27. 数学课上,李老师出示范了如下框中的题目.
小敏与同桌小聪讨论后,进行了如下解答:
(1)、特殊情况,探索结论当点E为AB的中点时,如图1,确定线段AE与DB的大小关系.请你直接写出结论:AEDB(填“>”、“<”或“=”);
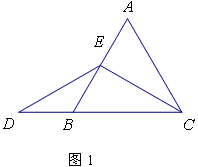 (2)、特例启发,解答题目
(2)、特例启发,解答题目解:题目中,AE与DB的大小关系是:AEDB(填“>”、“<”或“=”).理由如下:
如图2过点E作EF∥BC,交AC于点F;(请你完成以下解答过程)
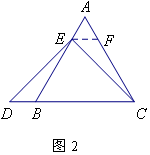 (3)、拓展结论,设计新题
(3)、拓展结论,设计新题在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).
28. 如图(1),矩形ABCD的一边BC在直角坐标系中x轴上,折叠边AD,使点D落在x轴上点F处,折痕为AE,已知AB=8,AD=10,并设点B坐标为(m,0),其中m>0.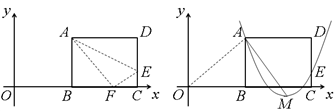 (1)、求点E、F的坐标(用含m的式子表示);(2)、连接OA,若△OAF是等腰三角形,求m的值;(3)、如图(2),设抛物线y=a(x-m-6)2+h经过A、E两点,其顶点为M,连接AM,若∠OAM=90°,求a、h、m的值.
(1)、求点E、F的坐标(用含m的式子表示);(2)、连接OA,若△OAF是等腰三角形,求m的值;(3)、如图(2),设抛物线y=a(x-m-6)2+h经过A、E两点,其顶点为M,连接AM,若∠OAM=90°,求a、h、m的值.