湖北省襄阳市枣阳市太平三中2020年数学中考模拟试卷
试卷更新日期:2020-04-01 类型:中考模拟
一、单选题
-
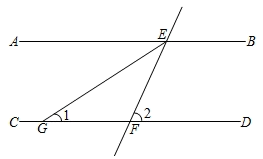
1. |﹣3|的相反数是( )A、﹣3 B、3 C、 D、﹣2. 若 ,则 的值是( )A、﹣2 B、2 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 如图,直线AB∥CD,直线EF分别交AB、CD于E、F两点,EG平分∠AEF,如果∠1=32°,那么∠2的度数是( )
 A、64° B、68° C、58° D、60°5. 一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面积为( )
A、64° B、68° C、58° D、60°5. 一个长方体的左视图、俯视图及相关数据如图所示,则其主视图的面积为( )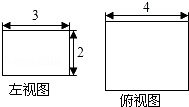 A、6 B、8 C、12 D、246. 二次根式 、 、 、 、 、 中,最简二次根式的概率是( )A、 B、 C、 D、7. 在平面直角坐标系中,已知点A(﹣2,3),若将OA绕原点O逆时针旋转180°得到OA',则点A'在平面直角坐标系中的位置是在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 函数y=ax+a与y= 在同一直角坐标系中的图象可能是( )A、
A、6 B、8 C、12 D、246. 二次根式 、 、 、 、 、 中,最简二次根式的概率是( )A、 B、 C、 D、7. 在平面直角坐标系中,已知点A(﹣2,3),若将OA绕原点O逆时针旋转180°得到OA',则点A'在平面直角坐标系中的位置是在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 函数y=ax+a与y= 在同一直角坐标系中的图象可能是( )A、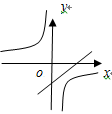 B、
B、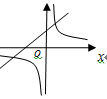 C、
C、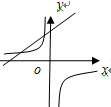 D、
D、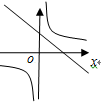 9. 甲、乙两人在相同的条件下,各射靶10次,经过计算:甲、乙射击成绩的平均数都是8环,甲的方差是1.2,乙的方差是2.8.下列说法中正确的是( )A、甲的众数与乙的众数相同 B、甲的成绩比乙稳定 C、乙的成绩比甲稳定 D、甲的中位数与乙的中位数相同10. 下列命题中是假命题的是( ).A、一组对边平行且相等的四边形是平行四边形 B、一组对边相等且有一个角是直角的四边形是矩形 C、一组邻边相等的平行四边形是菱形 D、一组邻边相等的矩形是正方形11. 已知△ABC内接于⊙O,若∠AOB=120°,则∠C的度数是( )A、60° B、120° C、60°或120° D、30°或150°12. 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:
9. 甲、乙两人在相同的条件下,各射靶10次,经过计算:甲、乙射击成绩的平均数都是8环,甲的方差是1.2,乙的方差是2.8.下列说法中正确的是( )A、甲的众数与乙的众数相同 B、甲的成绩比乙稳定 C、乙的成绩比甲稳定 D、甲的中位数与乙的中位数相同10. 下列命题中是假命题的是( ).A、一组对边平行且相等的四边形是平行四边形 B、一组对边相等且有一个角是直角的四边形是矩形 C、一组邻边相等的平行四边形是菱形 D、一组邻边相等的矩形是正方形11. 已知△ABC内接于⊙O,若∠AOB=120°,则∠C的度数是( )A、60° B、120° C、60°或120° D、30°或150°12. 已知二次函数y=ax2+bx+c的图象如图所示,有以下结论:①a+b+c<0;②a﹣b+c>1;③abc>0;④9a﹣3b+c<0;⑤c﹣a>1.其中所有正确结论的序号是( )
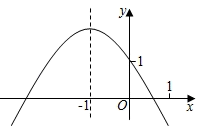 A、①② B、①③④ C、①②③④ D、①②③④⑤
A、①② B、①③④ C、①②③④ D、①②③④⑤二、填空题
-
13. 中华人民共和国国家统计局于2011年4月28日公布全国总人口为1370536875人,将1370536875用科学记数法保留三位有效数字,结果是.14. 两圆的直径分别为4和6,若两圆有唯一公共点,这两圆的圆心距是.15. 如图,EF过矩形ABCD对角线的交点O,且分别交AB、CD于E、F,若矩形ABCD的面积是12,那么阴影部分的面积是.
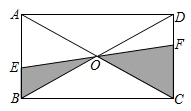 16. 目前甲型H1N1流感病毒在全球已有蔓延趋势,世界卫生组织提出各国要严加防控,因为曾经有一种流感病毒,若一人患了流感,经过两轮传染后共有81人患流感.如果设每轮传染中平均一个人传染x个人,那么可列方程为.17. 如图,圆锥的轴截面(过圆锥顶点和底面圆心的截面)是边长为4cm的等边三角形 ,点 是母线 的中点,一只蚂蚁从点 出发沿圆锥的表面爬行到点 处,则这只蚂蚁爬行的最短距离是cm.
16. 目前甲型H1N1流感病毒在全球已有蔓延趋势,世界卫生组织提出各国要严加防控,因为曾经有一种流感病毒,若一人患了流感,经过两轮传染后共有81人患流感.如果设每轮传染中平均一个人传染x个人,那么可列方程为.17. 如图,圆锥的轴截面(过圆锥顶点和底面圆心的截面)是边长为4cm的等边三角形 ,点 是母线 的中点,一只蚂蚁从点 出发沿圆锥的表面爬行到点 处,则这只蚂蚁爬行的最短距离是cm.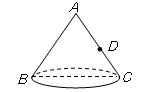
三、解答题
-
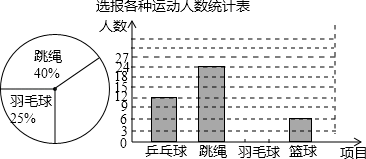
18. 请你先化简 ,再从-2,2, 中选择一个合适的a值代入求值.19. 某校为了提高学生身体素质,组织学生参加乒乓球、跳绳、羽毛球、篮球四项课外体育活动,要求学生根据自己的爱好只选报其中一项.学生会随机抽取了部分学生的报名表,并对抽取的学生的报名情况进行统计,绘制了两幅统计图(如图,不完整),请你结合图中的信息,解答下列问题:
 (1)、抽取的报名表的总数是多少?(2)、将两个统计图补充完整(不写计算过程);(3)、该校共有200人报名参加这四项课外体育活动,选报羽毛球的大约有多少人?20. 某校九年级学生去某处旅游,租用了若干辆汽车,如果每辆汽车坐45人,那么有15个学生无车可坐;如果每辆汽车坐60人,那么空出1辆汽车,其它汽车全部坐满.一共有多少名学生、多少辆汽车?21. 如图,矩形ABCD中,点E为AD上一点,∠BEC=90°,AB=2,DE=1,求BC的长.
(1)、抽取的报名表的总数是多少?(2)、将两个统计图补充完整(不写计算过程);(3)、该校共有200人报名参加这四项课外体育活动,选报羽毛球的大约有多少人?20. 某校九年级学生去某处旅游,租用了若干辆汽车,如果每辆汽车坐45人,那么有15个学生无车可坐;如果每辆汽车坐60人,那么空出1辆汽车,其它汽车全部坐满.一共有多少名学生、多少辆汽车?21. 如图,矩形ABCD中,点E为AD上一点,∠BEC=90°,AB=2,DE=1,求BC的长.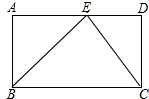 22. 小莉的爸爸买了一张唐梓山门票,她和哥哥两人都很想去观看,可门票只有一张,读九年级的哥哥想了一个办法,拿了八张扑克牌,将数字为1,2,3,4的四张牌给小莉,将数字为5,6,7,8的四张牌留给自己,并按如下游戏规则进行:小莉和哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌数字相加,如果和为偶数,则小莉去;如果和为奇数,则哥哥去.哥哥设计的游戏规则公平吗?若公平,请说明理由;若不公平,请你设计一种公平的游戏规则.23. 已知:如图,一次函数 的图象与反比例函数 ( )的图象交于点 . 轴于点 , 轴于点 . 一次函数的图象分别交 轴、 轴于点 、点 ,且 , .
22. 小莉的爸爸买了一张唐梓山门票,她和哥哥两人都很想去观看,可门票只有一张,读九年级的哥哥想了一个办法,拿了八张扑克牌,将数字为1,2,3,4的四张牌给小莉,将数字为5,6,7,8的四张牌留给自己,并按如下游戏规则进行:小莉和哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌数字相加,如果和为偶数,则小莉去;如果和为奇数,则哥哥去.哥哥设计的游戏规则公平吗?若公平,请说明理由;若不公平,请你设计一种公平的游戏规则.23. 已知:如图,一次函数 的图象与反比例函数 ( )的图象交于点 . 轴于点 , 轴于点 . 一次函数的图象分别交 轴、 轴于点 、点 ,且 , .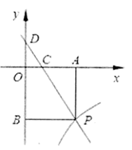 (1)、求点 的坐标;(2)、求一次函数与反比例函数的解析式;(3)、根据图象写出当 取何值时,一次函数的值小于反比例函数的值?24. “五一”前夕,某经销商计划花23500元购买A、B、C三种新款时装共50套进行试销,并且购进的C种时装套数不少于B种时装套数,且不超过A种时装套数,设购进A种时装x套,B种时装y套,三种时装的进价和售价如下表所示.
(1)、求点 的坐标;(2)、求一次函数与反比例函数的解析式;(3)、根据图象写出当 取何值时,一次函数的值小于反比例函数的值?24. “五一”前夕,某经销商计划花23500元购买A、B、C三种新款时装共50套进行试销,并且购进的C种时装套数不少于B种时装套数,且不超过A种时装套数,设购进A种时装x套,B种时装y套,三种时装的进价和售价如下表所示.型号
A
B
C
进价(元/套)
400
550
500
售价(元/套)
500
700
650
(1)、求y与x之间的函数关系式;(2)、满足条件的进货方案有哪几种?写出解答过程;(3)、假设所购进的这三种时装能全部卖出,且在购销这批时装的过程中需要另外支出各种费用1000元.通过计算判断哪种进货方案利润最大.25. 如图,AB是直经,D是 的中点,DE⊥AC交AC的延长线于E,⊙O的切线BF交AD的延长线于点F.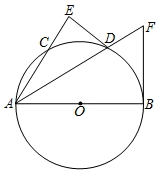 (1)、求证:DE是⊙O的切线.(2)、试探究AE,AD,AB三者之间的等量关系.(3)、若DE=3,⊙O的半径为5,求BF的长.26. 如图,等腰直角△OEF在坐标系中,有E(0,2),F(﹣2,0),将直角△OEF绕点E逆时针旋转90°得到△ADE,且A在第一象限内,抛物线y=ax2+bx+c经过点A,E.且2a+3b+5=0.
(1)、求证:DE是⊙O的切线.(2)、试探究AE,AD,AB三者之间的等量关系.(3)、若DE=3,⊙O的半径为5,求BF的长.26. 如图,等腰直角△OEF在坐标系中,有E(0,2),F(﹣2,0),将直角△OEF绕点E逆时针旋转90°得到△ADE,且A在第一象限内,抛物线y=ax2+bx+c经过点A,E.且2a+3b+5=0.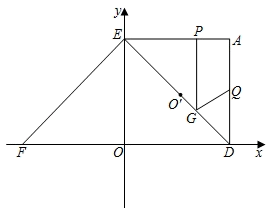 (1)、求抛物线的解析式.(2)、过ED的中点O'作O'B⊥OE于B,O'C⊥OD于C,求证:OBO'C为正方形.(3)、如果点P由E开始沿EA边以每秒2厘米的速度向点A移动,同时点Q由点A沿AD边以每秒1厘米的速度向点D移动,当点P移动到点A时,P,Q两点同时停止,且过P作GP⊥AE,交DE于点G,设移动的开始后为t秒.
(1)、求抛物线的解析式.(2)、过ED的中点O'作O'B⊥OE于B,O'C⊥OD于C,求证:OBO'C为正方形.(3)、如果点P由E开始沿EA边以每秒2厘米的速度向点A移动,同时点Q由点A沿AD边以每秒1厘米的速度向点D移动,当点P移动到点A时,P,Q两点同时停止,且过P作GP⊥AE,交DE于点G,设移动的开始后为t秒.①若S=PQ2(厘米),试写出S与t之间的函数关系式,并写出t的取值范围?
②当S取最小时,在抛物线上是否存在点R,使得以P,A,Q,R为顶点的四边形是平行四边形?如果存在,求出R的坐标;如果不存在,请说明理由.