湖北省黄石市2020年数学中考一模试卷
试卷更新日期:2020-04-01 类型:中考模拟
一、单选题
-
1. 下列各数是有理数的是( )A、 B、 C、 D、2. 地球与月球之间的距离约为38万千米,则38万用科学记数法表示为( )A、 B、 C、 D、3. 下列四个图形:
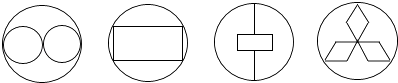
其中是轴对称图形,且对称轴的条数为2的图形的个数是( )
A、4 B、3 C、2 D、14. 如图是一个由5个完全相同的小正方体组成的立体图形,它的俯视图是( )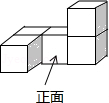 A、
A、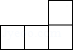 B、
B、 C、
C、 D、
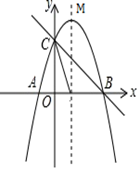
D、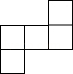 5. 使代数式 有意义的x的取值范围是( )A、 且 B、 C、 且 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 如图,在平面直角坐标系中, , , ,点P为 的外接圆的圆心,将 绕点O逆时针旋转 ,点P的对应点P’的坐标为( )
5. 使代数式 有意义的x的取值范围是( )A、 且 B、 C、 且 D、6. 下列运算正确的是( )A、 B、 C、 D、7. 如图,在平面直角坐标系中, , , ,点P为 的外接圆的圆心,将 绕点O逆时针旋转 ,点P的对应点P’的坐标为( ) A、 B、 C、 D、8. 已知如图,点 C 是线段 AB 的黄金分割点(AC>BC),则下列结论中正确的是( )
A、 B、 C、 D、8. 已知如图,点 C 是线段 AB 的黄金分割点(AC>BC),则下列结论中正确的是( ) A、AB2=AC2+BC2 B、BC2=AC•BA C、 D、9. 如图,在平面直角坐标系中,矩形OABC的面积为10,反比例函数 与AB、BC分别交于点D、E,若AD=2BD,则 的值为( )
A、AB2=AC2+BC2 B、BC2=AC•BA C、 D、9. 如图,在平面直角坐标系中,矩形OABC的面积为10,反比例函数 与AB、BC分别交于点D、E,若AD=2BD,则 的值为( ) A、 B、 C、 D、10. 如图,在边长为3的菱形ABCD中,点P从A点出发,沿A→B→C→D运动,速度为每秒3个单位;点Q同时从A点出发,沿A→D运动,速度为每秒1个单位,则 的面积S关于时间 的函数图象大致为( )
A、 B、 C、 D、10. 如图,在边长为3的菱形ABCD中,点P从A点出发,沿A→B→C→D运动,速度为每秒3个单位;点Q同时从A点出发,沿A→D运动,速度为每秒1个单位,则 的面积S关于时间 的函数图象大致为( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 在实数范围内分解因式: .12. 分式方程 的解为 .13. 如图所示,海面上有一座小岛A,一艘船在B处观测A位于西南方向20 km处,该船向正西方向行驶2小时至C处,此时观测A位于南偏东 ,则船行驶的路程约为 . (结果保留整数, , , )
 14. 甲、乙两位同学各抛掷一枚质地均匀的骰子,他们抛掷的点数分别记为 、 ,则 能被 整除的概率为 .15. 对两个不相等的实数根a、b,我们规定符号 表示a、b中较大的数,如: ,按照这个规定:方程 的解为 .16. 如图,已知点A1 , A2 , …,An均在直线 上,点B1 , B2 , …,Bn均在双曲线 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为 (n为正整数).若 ,则 , .
14. 甲、乙两位同学各抛掷一枚质地均匀的骰子,他们抛掷的点数分别记为 、 ,则 能被 整除的概率为 .15. 对两个不相等的实数根a、b,我们规定符号 表示a、b中较大的数,如: ,按照这个规定:方程 的解为 .16. 如图,已知点A1 , A2 , …,An均在直线 上,点B1 , B2 , …,Bn均在双曲线 上,并且满足:A1B1⊥x轴,B1A2⊥y轴,A2B2⊥x轴,B2A3⊥y轴,…,AnBn⊥x轴,BnAn+1⊥y轴,…,记点An的横坐标为 (n为正整数).若 ,则 , .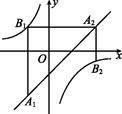
三、解答题
-
17. 计算: .18. 先化简,再求值: ,其中 满足 .19. 解不等式组: ,并求出所有整数解之和.20. 已知 是关于 的方程 的两个实数根.(1)、若 ,求实数 的取值范围;(2)、是否存在实数 使得 成立?若存在,请求出 的值;若不存在,请说明理由.21. 如图,在平行四边形ABCD中,AE、CF分别平分 、 .

求证:
(1)、AE=CF;(2)、AE∥CF.22. 某高校为了解本校学生出行使用共享单车的情况,随机调查了某天部分出行学生使用共享单车的情况,并整理成如下统计表.使用次数
0
1
2
3
4
5
人数
11
15
23
28
18
5
(1)、这天部分出行学生使用共享单车次数的中位数是 , 众数是 .(2)、这天33部分出行学生平均每人使用共享单车约多少次?(结果保留整数)(3)、若该校某天有1500名学生出行,请你估计这天使用共享单车次数在3次以上(含3次)的学生有多少名.23. 某商店打算以40元/千克的价格购进一批商品,经市场调查发现,该商品的销售量 (千克)与售价 (元)之间的关系如下表:x
45
50
55
60
......
y
190
180
170
160
......
(1)、求 关于 的函数关系式;(2)、若要控制成本不超过3200元的情况下,保证利润达到3200元,该如何定价?