湖北省黄冈市2020年数学中考模拟试卷(三)
试卷更新日期:2020-04-01 类型:中考模拟
一、单选题
-
1. ( )A、4 B、-4 C、2 D、-22. 下列计算中,正确的是( )A、 B、 C、 D、3. 某企业2017年总收入约为7380000元,这一数据用科学记数法表示为( )A、7.38×104元 B、73.8×105元 C、7.38×106元 D、0.738×106元4. 下列图形中,既是中心对称图形,又是轴对称图形的是( )A、矩形 B、三角形 C、平行四边形 D、等腰梯形5. 在一次歌唱比赛中,10名评委给某一歌手打分如下表:
成绩(分)
8.9
9.3
9.4
9.5
9.7
9.8
评委(名)
1
2
1
4
1
1
则这名歌手成绩的中位数和众数分别是( )
A、9.3, 2 B、9.5 ,4 C、9.5,9.5 D、9.4 ,9.56. 一个底面直径为2,高为3的圆锥的体积是( )A、π B、2π C、3π D、4π7. 如图的几何体是由六个完全相同的正方体组成的,这个几何体的主视图是( )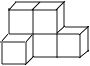 A、
A、 B、
B、 C、
C、 D、
D、 8. 一个菱形的四个内角度数之比依次为1:2:3:4,这个事件是( )A、必然事件 B、随机事件 C、不可能事件 D、以上都不是9. 关于x的分式方程 = 有解,则字母a的取值范围是( )A、a=5或a=0 B、a≠0 C、a≠5 D、a≠5且a≠010. 将矩形 沿对角线 折叠,使得 与 重合,若 ,则 ( )
8. 一个菱形的四个内角度数之比依次为1:2:3:4,这个事件是( )A、必然事件 B、随机事件 C、不可能事件 D、以上都不是9. 关于x的分式方程 = 有解,则字母a的取值范围是( )A、a=5或a=0 B、a≠0 C、a≠5 D、a≠5且a≠010. 将矩形 沿对角线 折叠,使得 与 重合,若 ,则 ( ) A、1 B、2 C、3 D、411. 如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )
A、1 B、2 C、3 D、411. 如图,已知AB、CD、EF都与BD垂直,垂足分别是B、D、F,且AB=1,CD=3,那么EF的长是( )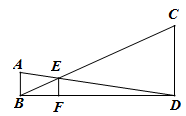 A、 B、 C、 D、12.
A、 B、 C、 D、12.如图,点P是定线段OA上的动点,点P从O点出发,沿线段OA运动至点A后,再立即按原路返回至点O停止,点P在运动过程中速度大小不变,以点O为圆心,线段OP长为半径作圆,则该圆的周长l与点P的运动时间t之间的函数图象大致为( )
 A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
13. 分解因式:14. 一个不透明的袋子里装有除颜色不同外其他都相同的5个小球,其中红球3个、白球2个,一次从中摸出两个小球,全是红球的概率为 .15. 如图,⊙O的半径为1cm,正六边形ABCDEF内接于⊙O,则图中阴影部分面积为 cm2 . (结果保留π)
 16. 对于反比例函数 ,下列说法:①点 在它的图象上;②它的图象在第一、三象限;③当 时, 随 的增大而增大;④当 时,随 的增大而减小.上述说法中,正确的序号是.(填上所有你认为正确的序号)17. 观察下列等式:
16. 对于反比例函数 ,下列说法:①点 在它的图象上;②它的图象在第一、三象限;③当 时, 随 的增大而增大;④当 时,随 的增大而减小.上述说法中,正确的序号是.(填上所有你认为正确的序号)17. 观察下列等式:12×231=132×21,
13×341=143×31,
23×352=253×32,
34×473=374×43,
62×286=682×26,
…………………….
以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”.
根据上述规律填空:27×=×.
三、解答题
-
18. 如图,在正方形 中,点 在对角线 上,点 在边 上,连接 、 , 交对角线 于点 ,且 .
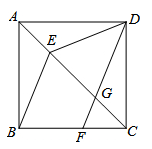 (1)、求证: ;(2)、试判断 和 的位置关系,并说明理由.19. 学校准备在各班设立图书角以丰富同学们的课余文化生活,为了更合理的搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:
(1)、求证: ;(2)、试判断 和 的位置关系,并说明理由.19. 学校准备在各班设立图书角以丰富同学们的课余文化生活,为了更合理的搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图1和图2提供的信息,解答下列问题:
 (1)、在这次抽样调查中,一共调查了多少名学生;(2)、请把折线统计图(图1)补充完整;(3)、求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;(4)、如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数;(5)、学校若在喜爱艺术、文学、科普、体育四类中任意抽取两类建立兴趣小组,求出恰好选中是体育和科普两类的概率.20. 如图,点 在双曲线上, 垂直 轴,垂足为 ,点 在 上, 平行于 轴交曲线于点 ,直线 与 轴交于点 ,已知 ,点 的坐标为 .
(1)、在这次抽样调查中,一共调查了多少名学生;(2)、请把折线统计图(图1)补充完整;(3)、求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;(4)、如果这所中学共有学生1800名,那么请你估计最喜爱科普类书籍的学生人数;(5)、学校若在喜爱艺术、文学、科普、体育四类中任意抽取两类建立兴趣小组,求出恰好选中是体育和科普两类的概率.20. 如图,点 在双曲线上, 垂直 轴,垂足为 ,点 在 上, 平行于 轴交曲线于点 ,直线 与 轴交于点 ,已知 ,点 的坐标为 .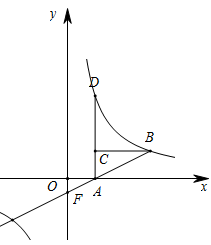 (1)、求该双曲线的解析式;(2)、求 的面积.21. 如图,在 中, , 的垂直平分线分别与 , 及 的延长线相交于点 , , ,且 . ⊙O是 的外接圆, 的平分线交 于点 ,交⊙O于点 ,连接 , .
(1)、求该双曲线的解析式;(2)、求 的面积.21. 如图,在 中, , 的垂直平分线分别与 , 及 的延长线相交于点 , , ,且 . ⊙O是 的外接圆, 的平分线交 于点 ,交⊙O于点 ,连接 , . (1)、求证: ;(2)、试判断 与⊙O的位置关系,并说明理由;(3)、若 , 求 的值.22. 如图,经过原点的抛物线y=﹣x2﹣2mx(m>1)与x轴的另一个交点为A.过点P(﹣1,m)作直线PD⊥x轴于点D,交抛物线于点B,BC∥x轴交抛物线于点C.
(1)、求证: ;(2)、试判断 与⊙O的位置关系,并说明理由;(3)、若 , 求 的值.22. 如图,经过原点的抛物线y=﹣x2﹣2mx(m>1)与x轴的另一个交点为A.过点P(﹣1,m)作直线PD⊥x轴于点D,交抛物线于点B,BC∥x轴交抛物线于点C. (1)、当m=2时.
(1)、当m=2时.①求线段BC的长及直线AB所对应的函数关系式;
②若动点Q在直线AB上方的抛物线上运动,求点Q在何处时,△QAB的面积最大?
③若点F在坐标轴上,且PF=PC,请直接写出符合条件的点F在坐标;
(2)、当m>1时,连接CA、CP,问m为何值时,CA⊥CP?