湖北省恩施市崔坝、沙地、双河、新塘四校2019-2020学年七年级下学期数学第一次月考试卷

试卷更新日期：2020-04-01 类型：月考试卷

进入出卷网下载

一、单选题

1. 2018年5月3日，中国科学院在上海发布了中国首款人工智能芯片：寒武纪（MLU100），该芯片在平衡模式下的等效理论峰值速度达每秒128 000 000 000 000次定点运算，将数
128 000 000 000 000用科学记数法表示为（）

A、 1.28 $\times$ 10¹⁴ B、1.28 $\times$ 10^-14 C、128 $\times$ 10¹² D、0.128 $\times$ 10¹¹

查看试题解析
2. 某潜水艇停在海面下500米处，先下降200米，又上升130米，这时潜水艇停在海面下多少米处（）

A、430 B、530 C、570 D、470

查看试题解析
3. 下列说法：①整数和分数统称为有理数；②绝对值是它本身的数只有0；③两数之和一定大于每个加数；④如果两个数积为0，那么至少有一个因数为0；⑤0是最小的有理数，其中正确的个数是（）

A、2个 B、3个 C、4个 D、5个

查看试题解析
4. 关于单项式2³x²y²z，下列结论正确的是（）

A、系数是-2，次数是 4 B、系数是-2，次数是 5 C、系数是-2，次数是 8 D、系数是 2³ ，次数是 5

查看试题解析
5. 若数轴上点A、B分别表示数2、﹣2，则A、B两点之间的距离可表示为（）

A、2+（﹣2） B、2﹣（﹣2） C、（﹣2）+2 D、（﹣2）﹣2

查看试题解析
6. 下列算式中，运算结果为负数的是（）

A、|-1| B、(-2)³ C、(-1)×(-2) D、(-3)²

查看试题解析
7. 按括号内的要求用四舍五人法取近似数，下列正确的是（）

A、403.53≈403（精确到个位） B、2.604≈2.60（精确到十分位） C、0.0296≈0.03（精确到0.01） D、0.0136≈0.014（精确到0.0001）

查看试题解析
8. 如图，a、b 两个数在数轴上的位置如图所示，则下列各式正确的是（）

A、a+b＜0 B、ab＜0 C、b﹣a＜0 D、 $\frac{b}{a}$ >0

查看试题解析
9. 一组按规律排列的多项式：ab，a²b³ ， a³b⁵ ， a⁴b⁷ ， ⋯⋯，其中第 10 个式子是（）

A、a¹⁰ b¹⁵ B、a¹⁰ b¹⁹ C、a¹⁰ b¹⁷ D、a¹⁰ b²¹

查看试题解析
10. 已知|a|=5，b³=﹣27，且a＞b，则a﹣b值为（）

A、2 B、﹣2或8 C、8 D、﹣2

查看试题解析
11. 我国是最早认识负数，并进行相关运算的国家.在古代数学名著《九章算术》里，就记载了利用算筹实施“正负术”的方法，图1表示的是计算3+(﹣4)的过程.按照这种方法，图2表示的过程应是在计算（）

A、(﹣5)+(﹣2) B、(﹣5)+2 C、5+(﹣2) D、5+2

查看试题解析
12. 下列说法：①若|a|=a，则a=0；②若a，b互为相反数，且ab≠0，则 $\frac{b}{a}$ =﹣1；③若a²=b² ，则a=b；④若a＜0，b＜0，则|ab﹣a|=ab﹣a．其中正确的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 如果 ${(x - 6)}^{2} + | y - 2 | = 0$ ，则 x-y= .

查看试题解析
14. 已知3x－8与2互为相反数，则x＝．

查看试题解析
15. 如果多项式 x⁴－（a－1）x³＋3x²－（b＋1）x－1 中不含 x³ 和 x 项，则 a＝， b＝.

查看试题解析
16. 观察下列各式： $\frac{1}{1 \times 3} = \frac{1}{2} (1 - \frac{1}{3})$ ， $\frac{1}{3 \times 5} = \frac{1}{2} (\frac{1}{3} - \frac{1}{5})$ ， $\frac{1}{5 \times 7} = \frac{1}{2} (\frac{1}{5} - \frac{1}{7})$ ，…，根据观察计算： $\frac{1}{1 \times 3} + \frac{1}{3 \times 5} + \frac{1}{5 \times 7} + \dots + \frac{1}{(2 n - 1) (2 n + 1)}$ ＝.（n为正整数）

查看试题解析
17. 请你把下列各数填入表示它所在的数集的圈里：
﹣2，﹣20%，﹣0.13，﹣7 $\frac{3}{4}$ ，10， $\frac{1}{4}$ ，21，6.2，4.7，﹣8

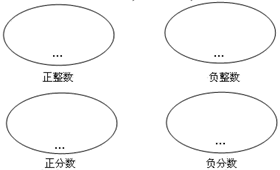
这四个集合合并在一起填(“是”或“不是”）全体有理数集合，若不是，缺少的是.

查看试题解析

三、解答题

18. 计算：

(1)、﹣20+（﹣14）﹣（﹣18）﹣13

(2)、4﹣8×（﹣ $\frac{1}{2}$ ）³

(3)、 $(- \frac{3}{4} - \frac{5}{9} + \frac{7}{12}) \div \frac{1}{36}$

(4)、 $| - \frac{7}{9} | \div (\frac{2}{3} - \frac{1}{5}) - \frac{1}{3} \times {(- 4)}^{2}$

查看试题解析
19. 有一列数： $\frac{1}{2}$ ，1，3，﹣3，﹣1，﹣2.5；

(1)、画一条数轴，并把上述各数在数轴上表示出来；

(2)、把这一列数按从小到大的顺序排列起来，并用“＜”连接.

查看试题解析
20. 如图所示，其中长方形的长为a，宽为b.

(1)、图中阴影部分的面积是多少？

(2)、你能判断它是单项式或多项式吗？它的次数是多少？

查看试题解析
21. 有理数a、b、c在数轴上的位置如图，化简：|b|-|a|+|c|的值.

查看试题解析
22. 若 $a$ 、 $b$ 互为相反数， $c$ 、 $d$ 互为倒数， $m$ 的绝对值是 $2$ .

(1)、分别直接写出 $a + b$ ， $c d$ ， $m$ 的值；

(2)、求 $m + c d + \frac{a + b}{m}$ 的值.

查看试题解析
23. 一辆货车从超市出发，向东走了3千米到达小彬家，继续走2.5米到达小颖家，然后向西走了10千米到达小明家，最后回到超市.

(1)、小明家距小彬家多远？

(2)、货车一共行驶了多少千米？

(3)、货车每千米耗油0.2升，这次共耗油多少升？

查看试题解析
24. 已知数轴上有A、B、C三点，分别表示有理数－26，－10，10，动点P从A出发，以每秒1个单位的速度向终点C移动，设点P移动时间为t秒.

(1)、用含t的代数式表示P到点A和点C的距离：PA= ， PC=。

(2)、当点P运动到B点时，点Q从A点出发，以每秒3个单位的速度向C点运动，Q点到达C点后，再立即以同样的速度返回，当点P运动到点C时，P、Q两点运动停止，
①当P、Q两点运动停止时，求点P和点Q的距离；

②求当t为何值时P、Q两点恰好在途中相遇.

查看试题解析