浙江省金华十校联考2016-2017学年高一上学期数学期末考试试卷
试卷更新日期:2017-08-31 类型:期末考试
一、选择题
-
1. 设全集U={1,2,3,4,5,6,7,8},集合S={1,3,5},T={3,6},则∁U(S∪T)等于( )A、∅ B、{2,4,7,8} C、{1,3,5,6} D、{2,4,6,8}2. cos210°=( )A、﹣ B、﹣ C、 D、3. 函数y=f(x)和x=2的交点个数为( )A、0个 B、1个 C、2个 D、0个或1个4. 已知扇形的半径为2,面积为4,则这个扇形圆心角的弧度数为( )A、 B、2 C、2 D、25. 如果lgx=lga+3lgb﹣5lgc,那么( )A、x=a+3b﹣c B、 C、 D、x=a+b3﹣c36. 已知sin = ,cos =﹣ ,则角α终边所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 函数 的图象为( )A、
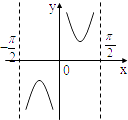 B、
B、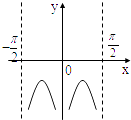 C、
C、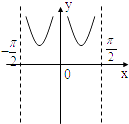 D、
D、 8. 已知函数f(x)=ax2+2ax+4(0<a<3),若x1<x2 , x1+x2=1﹣a,则( )A、f(x1)<f(x2) B、f(x1)>f(x2) C、f(x1)=f(x2) D、f(x1)<f(x2)和f(x1)=f(x2)都有可能9. 已知函数f(x)=sin(ωx﹣ )( <ω<2),在区间(0, )上( )A、既有最大值又有最小值 B、有最大值没有最小值 C、有最小值没有最大值 D、既没有最大值也没有最小值10. 已知f(x)=loga(a﹣x+1)+bx(a>0,a≠1)是偶函数,则( )A、b= 且f(a)>f( ) B、b=﹣ 且f(a)<f( ) C、b= 且f(a+ )>f( ) D、b=﹣ 且f(a+ )<f( )
8. 已知函数f(x)=ax2+2ax+4(0<a<3),若x1<x2 , x1+x2=1﹣a,则( )A、f(x1)<f(x2) B、f(x1)>f(x2) C、f(x1)=f(x2) D、f(x1)<f(x2)和f(x1)=f(x2)都有可能9. 已知函数f(x)=sin(ωx﹣ )( <ω<2),在区间(0, )上( )A、既有最大值又有最小值 B、有最大值没有最小值 C、有最小值没有最大值 D、既没有最大值也没有最小值10. 已知f(x)=loga(a﹣x+1)+bx(a>0,a≠1)是偶函数,则( )A、b= 且f(a)>f( ) B、b=﹣ 且f(a)<f( ) C、b= 且f(a+ )>f( ) D、b=﹣ 且f(a+ )<f( )二、填空题
-
11. 已知角α的终边过点P(﹣8m,﹣6sin30°),且cosα=﹣ ,则m的值为 , sinα= .12. 计算lg4+lg500﹣lg2= , +(log316)•(log2 )= .13. 已知sinα= +cosα,且α∈(0, ),则sin2α= , cos2α= .14. 如果幂函数f(x)的图象经过点(2,8),则f(3)= . 设g(x)=f(x)+x﹣m,若函数g(x)在(2,3)上有零点,则实数m的取值范围是 .15. 已知tan(π﹣x)=﹣2,则4sin2x﹣3sinxcosx﹣5cos2x= .16. 已知函数f(x)=﹣2sin(2x+φ)(|φ|<π),若 是f(x)的一个单调递增区间,则φ的取值范围为 .17. 已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=2x﹣x2 , 若存在实数a,b,使f(x)在[a,b]上的值域为[ , ],则ab= .
三、解答题
-
18. 函数f(x)= 的定义域为集合A,函数g(x)=x﹣a(0<x<4)的值域为集合B.
(Ⅰ)求集合A,B;
(Ⅱ)若集合A,B满足A∩B=B,求实数a的取值范围.
19. 设函数f(x)=Asin(ωx+φ)(A>0,ω>0,﹣ <φ< ,x∈R)的部分图象如图所示.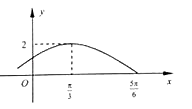
(Ⅰ)求函数y=f(x)的解析式;
(Ⅱ)将函数y=f(x)的图象沿x轴方向向右平移 个单位长度,再把横坐标缩短到原来的 (纵坐标不变),得到函数y=g(x)的图象,当x∈[﹣ , ]时,求函数g(x)的值域.
20. 已知函数f(x)=lg .(Ⅰ)求函数f(x)的定义域,并证明其在定义域上是奇函数;
(Ⅱ)对于x∈[2,6],f(x)>lg 恒成立,求m的取值范围.