广西来宾市忻城县2018-2019学年八年级下学期数学期中考试试卷
试卷更新日期：2020-04-01 类型：期中考试
一、单选题
-
1. 已知在△ABC中，∠ACB＝90° ，∠A＝60°，则∠B的度数是（ ）
A、30° B、35° C、40° D、50°2. 在Rt△ABC中，∠C＝90°，a＝8，c＝17，则b的长是（ ）A、25 B、 C、15 D、133. 如图，在 中， ， ， ， 平分 ，则点 到 的距离等于（ ）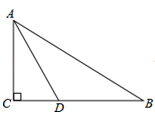
A、3 B、4 C、5 D、94. 如图，在Rt△ABC中，CD是斜边AB上的中线，若∠A＝26°，则∠BDC的度数是（ ）
A、26° B、38° C、42° D、52°5. 如图，在Rt△ABC中，∠C＝90°，∠A＝30°，D是AC边的中点，DE⊥AC于点D，交AB于点E，若AB＝16，则DE的长是（ ）
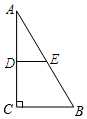A、8 B、6 C、4 D、26. 在三边分别为下列长度的三角形中，不能组成直角三角形的是（ ）A、4，7，5 B、2，3， C、5，13，12 D、1， ，7. 若一个正多边形的每一个内角为156°，则这个正多边形的边数是（ ）A、14 B、15 C、16 D、178. 从n边形的一个顶点出发作对角线，这些对角线把这个n边形分成的三角形个数为（ ）A、（n+1）个 B、n个 C、（n﹣1）个 D、（n﹣2）个9. 将一个n边形变成(n＋1)边形，内角和将( )A、减少180° B、增加90° C、增加180° D、增加360°10. 下列说法中能判定四边形是矩形的是（ ）A、有两个角为直角的四边形 B、对角线互相平分的四边形 C、对角线相等的四边形 D、四个角都相等的四边形11. 下列图形：①平行四边形；②矩形；③菱形；④等边三角形中，是中心对称图形的有（ ）A、①②③ B、②③④ C、①②④ D、①②③④12. 如图，点P是边长为2的菱形ABCD对角线AC上的一个动点，点E、F分别是边AB、BC的中点，则PE+PF的最小值是（ ）
A、1 B、2 C、2 D、4二、填空题
-
13. 如图，在△ABC中，∠ACB＝90°，∠A＝30°，D是AB的中点，BC＝3，则CD＝.
14. 一个多边形的内角和是720°，这个多边形的边数是 ．15. 如图，在▱ABCD中，EC平分∠BCD，交AD边于点E，AE＝3，BC＝5，则AB的长等于.
16. 如图，在矩形ABCD中，AC是对角线，且∠ACD＝60°，AB＝2，则矩形ABCD的面积等于.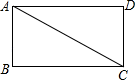
17. 如图，点E在正方形ABCD的边BA的延长线上，连接AC，AC＝AE，CE交AD于点F，则∠ACE的度数等于.
18. 如图，在菱形ABCD中，点E、F、G、H分别是AB、BC、CD、AD的中点，EF＝2EH，则AB与EH的数量关系是AB＝EH.
三、解答题
-
19. 如图，点A、B、C、D在同一直线上，∠E＝∠F＝90°，AE＝BF，AB＝CD，求证：∠ACE＝∠BDF.
20. 如图，在▱ABCD中，点E、F分别在AD、BC上，且AE＝CF.
(1)、求证：△AEB≌△CFD；(2)、求证：四边形BFDE是平行四边形.21. 如图，在△ABC中，∠C＝90°，AC＝BC，AD平分∠BAC交BC于点D，过点D作DE⊥AB，垂足为E.
(1)、求证：AC＝AE；(2)、若△BDE的周长为20，求AB的长.22. 如图，BD是▱ABCD的对角线，点E、F分别在BD上，连接AE、CF.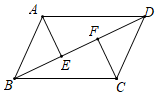
(1)、请你添加一个条件，使△AED≌△CFB，并给予证明；(2)、在你添加的条件后，不再添加其它条件，写出图中所有全等的三角形.23.如图，AC是▱ABCD的一条对角线，过AC中点O的直线分别交AD，BC于点E，F．
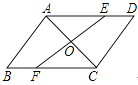(1)、求证：△AOE≌△COF；
(2)、当EF与AC满足什么条件时，四边形AFCE是菱形？并说明理由．24. 如图，在矩形ABCD中，对角线AC与BD交于点O，DE∥AC交BA的延长线于点E.
(1)、求证：BD＝DE；(2)、若∠ACB＝30°，BD＝8，求四边形BCDE的面积.
