广西合浦县2018-2019学年八年级下学期数学期中考试试卷
试卷更新日期:2020-04-01 类型:期中考试
一、单选题
-
1. 如图,图形中是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 在一个直角三角形中,有一个锐角等于 ,则另一个锐角的度数是( )A、 B、 C、 D、3. 以下说法正确的是( )A、各边都相等的多边形是正多边形 B、到线段两个端点距离相等的点在线段的垂直平分线上 C、角的平分线就是角的对称轴 D、形状相同的两个三角形是全等三角形4. 一个正多边形的内角和是540°,则这个正多边形的边数是( )A、4 B、5 C、6 D、75. 如图,在给定的一张平行四边形纸片上按如下操作:连结 ,作 的垂直平分线 分别交 , , 于 , , ,连结 , ,则四边形 是( )
2. 在一个直角三角形中,有一个锐角等于 ,则另一个锐角的度数是( )A、 B、 C、 D、3. 以下说法正确的是( )A、各边都相等的多边形是正多边形 B、到线段两个端点距离相等的点在线段的垂直平分线上 C、角的平分线就是角的对称轴 D、形状相同的两个三角形是全等三角形4. 一个正多边形的内角和是540°,则这个正多边形的边数是( )A、4 B、5 C、6 D、75. 如图,在给定的一张平行四边形纸片上按如下操作:连结 ,作 的垂直平分线 分别交 , , 于 , , ,连结 , ,则四边形 是( ) A、菱形 B、矩形 C、正方形 D、无法判断6. 如图,一根竹竿 ,斜靠在竖直的墙上, 是 中点, 表示竹竿 端沿墙上、下滑动过程中的某个位置,则在竹竿 滑动过程中 ( )
A、菱形 B、矩形 C、正方形 D、无法判断6. 如图,一根竹竿 ,斜靠在竖直的墙上, 是 中点, 表示竹竿 端沿墙上、下滑动过程中的某个位置,则在竹竿 滑动过程中 ( ) A、下滑时, 增大 B、上升时, 减小 C、只要滑动, 就变化 D、无论怎样滑动, 不变7. 如图,在 中, , , 分别为 , , 边的中点, 于 , ,则 等于( )
A、下滑时, 增大 B、上升时, 减小 C、只要滑动, 就变化 D、无论怎样滑动, 不变7. 如图,在 中, , , 分别为 , , 边的中点, 于 , ,则 等于( ) A、8 B、10 C、12 D、168. 在 中, , 于 , 平分 交 于 ,则下列结论一定成立的是( )
A、8 B、10 C、12 D、168. 在 中, , 于 , 平分 交 于 ,则下列结论一定成立的是( )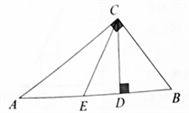 A、 B、 C、 D、9. 如图,在 中, , , 于 , 是 的平分线,且交 于 ,如果 ,则 的长为( )
A、 B、 C、 D、9. 如图,在 中, , , 于 , 是 的平分线,且交 于 ,如果 ,则 的长为( ) A、2 B、4 C、6 D、810. 如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )
A、2 B、4 C、6 D、810. 如图,在平行四边形ABCD中,∠BAD的平分线交BC于点E,∠ABC的平分线交AD于点F,若BF=12,AB=10,则AE的长为( )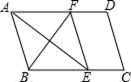 A、10 B、12 C、16 D、18
A、10 B、12 C、16 D、18二、填空题
-
11.
如图,有一个与地面成30°角的斜坡,现要在斜坡上竖一电线杆,当电线杆与地面垂直时,它与斜坡所成的角α=°.
 12. 如图,在 中, ,CD是 的平分线,若 ,则D到AC的距离为.
12. 如图,在 中, ,CD是 的平分线,若 ,则D到AC的距离为. 13. 一个多边形的内角和与外角和相等,则这个多边形的对角线条数是.14. 如图, 为等腰直角三角形, , 为等边三角形,则 .
13. 一个多边形的内角和与外角和相等,则这个多边形的对角线条数是.14. 如图, 为等腰直角三角形, , 为等边三角形,则 . 15. 如图,在 中, , , 是 的中点,点 在 的延长线上,连接 ,若 ,则 的长为.
15. 如图,在 中, , , 是 的中点,点 在 的延长线上,连接 ,若 ,则 的长为.
三、解答题
-
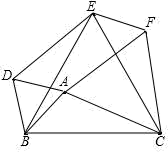
16. 如图,在 中, 、 分别是 、 边上的中线,若 , ,且 的周长为15,求 的长.
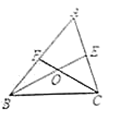 17.
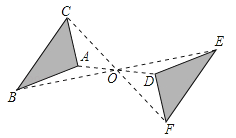
17.如图,△ABC与△DEF关于点O对称,请你写出两个三角形中的对称点,相等的线段,相等的角.
 18. 如图,在平行四边形ABCD中,对角线AC与BD相交于点O,△ABO是等边三角形,AB=6,求BC的长.
18. 如图,在平行四边形ABCD中,对角线AC与BD相交于点O,△ABO是等边三角形,AB=6,求BC的长. 19. 如图所示,在 中, , , 为 延长线上一点,点 在 上,且 .求证: .
19. 如图所示,在 中, , , 为 延长线上一点,点 在 上,且 .求证: . 20. 如图,在 中, , , 平分 , 于点 , 的延长线交 于点 , 为 的中点,求 的长.
20. 如图,在 中, , , 平分 , 于点 , 的延长线交 于点 , 为 的中点,求 的长. 21. 如图,在 中, ,点 是 中点, , .
21. 如图,在 中, ,点 是 中点, , . (1)、求证:四边形 是菱形;(2)、过点 作 于点 , , ,求 的长.
(1)、求证:四边形 是菱形;(2)、过点 作 于点 , , ,求 的长.