吉林省长春市2019年中考数学五模考试试卷
试卷更新日期:2020-03-30 类型:中考模拟
一、单选题
-
1. 在实数﹣2,1,0,﹣3中,最小的数是( )A、﹣2 B、1 C、0 D、﹣32. 某市2019市2月5日至2月12日春节期间,道路旅客运输车辆安全发送旅客41497人次,道路旅客运输秩序总体平稳,安全生产情况良好,无旅客滞留情况.数据41497用科学记数法表示为( )A、 B、 C、 D、3. 如图,智博会上使用的演讲台俯视图是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 不等式组 ,的解集是( )A、 B、 C、 D、5. 边长相等的正方形与正六边形按如图方式拼接在一起,则 的度数为( )
4. 不等式组 ,的解集是( )A、 B、 C、 D、5. 边长相等的正方形与正六边形按如图方式拼接在一起,则 的度数为( ) A、 B、 C、 D、6. 如图,把一张长方形的纸片ABCD沿EF折叠,若∠AED′=40°,则∠DEF的度数为( )
A、 B、 C、 D、6. 如图,把一张长方形的纸片ABCD沿EF折叠,若∠AED′=40°,则∠DEF的度数为( ) A、40° B、50° C、60° D、70°7. 如图,小明为了测量校园里旗杆 的高度,将测角仪 竖直放在距旗杆底部 点 的位置,在 处测得旗杆顶端 的仰角为 ,若测角仪的高度是 ,则旗杆 的高度约为(精确到 ,参考数据: , , )( )
A、40° B、50° C、60° D、70°7. 如图,小明为了测量校园里旗杆 的高度,将测角仪 竖直放在距旗杆底部 点 的位置,在 处测得旗杆顶端 的仰角为 ,若测角仪的高度是 ,则旗杆 的高度约为(精确到 ,参考数据: , , )( ) A、8.5米 B、9米 C、9.5米 D、10米8. 如图,在第一象限内,点P(2,3)、M(a,2)是双曲线 上的两点,PA⊥x轴于点A,MB⊥x轴于点B,PA与OM交于点C,则△OAC的面积为( )
A、8.5米 B、9米 C、9.5米 D、10米8. 如图,在第一象限内,点P(2,3)、M(a,2)是双曲线 上的两点,PA⊥x轴于点A,MB⊥x轴于点B,PA与OM交于点C,则△OAC的面积为( ) A、1. B、3. C、2. D、 .
A、1. B、3. C、2. D、 .二、填空题
-
9. 计算: .10. 已知一组数据2,6,5,2,4,则这组数据的中位数是 .11. 分解因式: .12. 如图, 是 的直径,点 、 在 上,若 ,则 .
 13. 如图,在 中, , ,以点 为圆心,以任意长为半径作弧,分别交 、 于点 、 ,再分别以点 、 为圆心,以大于 的长为半径作弧,两弧在 内交于点 ,连结 并延长,交 于点 ,则 的长为.
13. 如图,在 中, , ,以点 为圆心,以任意长为半径作弧,分别交 、 于点 、 ,再分别以点 、 为圆心,以大于 的长为半径作弧,两弧在 内交于点 ,连结 并延长,交 于点 ,则 的长为.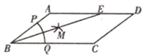
三、解答题
-
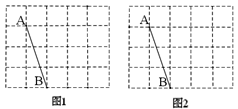
14. 先化简,再求值: ,其中 .15. 在学校组织的朗诵比赛中,甲、乙两名学生以抽签的方式从3篇不同的文章中抽取一篇参加比赛,抽签规则是:在3个相同的标签上分别标注字母A、B、C,各代表1篇文章,一名学生随机抽取一个标签后放回,另一名学生再随机抽取.用画树状图或列表的方法列出所有等可能的结果,并求甲、乙抽中同一篇文章的概率.16. 我国古代数学著作《九章算术》中有如下问题:“今有牛五,羊二,直金十二两.牛二,羊五,直金九两,牛羊各直金几何?”意思是:5头牛,2只羊共价值12两“金”.2头牛,5只羊共价值9两“金”.求每头牛,每只羊各价值多少两“金”?17. 图1、图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AB的两个端点均在小正方形的顶点上.(1)、在图1中画出一个以AB为一边面积为 5的等腰RtABC,且点C在小正方形顶点上;(2)、在图2中画出一个以AB为一边面积为 4的平行四边形ABDE,且点D和点E均在小正方形的顶点上;写出所画四边形周长=.
 18. 如图,在 中, ,以 为直径的 交 于点 ,过点 作 于点 .
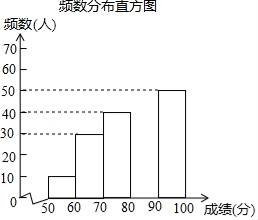
18. 如图,在 中, ,以 为直径的 交 于点 ,过点 作 于点 . (1)、求证:直线 是 的切线;(2)、若 , ,求 的值.19. 中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
(1)、求证:直线 是 的切线;(2)、若 , ,求 的值.19. 中华文明,源远流长;中华汉字,寓意深广.为传承中华优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,校团委随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:频数频率分布表
成绩x(分)
频数(人)
频率
50≤x<60
10
0.05
60≤x<70
30
0.15
70≤x<80
40
n
80≤x<90
m
0.35
90≤x≤100
50
0.25
根据所给信息,解答下列问题:
(1)、m= , n=;(2)、补全频数分布直方图;(3)、这200名学生成绩的中位数会落在分数段;(4)、若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的3000名学生中成绩是“优”等的约有多少人?20. 某种机器在加工零件的过程中,机器的温度会不断变化.当机器温度升高至 时,机器会自动启动冷却装置控制温度上升的速度;当温度升到 时,机器自动停止加工零件,冷却装置继续工作进行降温;当温度恢复至 时,机器自动开始继续加工零件,如此往复,机器从 时开始,机器的温度 ( )随时间 (分)变化的函数图象如图所示. (1)、当机器的温度第一次从 升至 时,求 与 之间的函数关系式;(2)、冷却装置将机器温度第一次从 降至 时,需要多少分钟?(3)、机器的温度在 以上(含 )时,机器会自动发出鸣叫进行报警.当 时,直接写出机器的鸣叫时间.21. 如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC
(1)、当机器的温度第一次从 升至 时,求 与 之间的函数关系式;(2)、冷却装置将机器温度第一次从 降至 时,需要多少分钟?(3)、机器的温度在 以上(含 )时,机器会自动发出鸣叫进行报警.当 时,直接写出机器的鸣叫时间.21. 如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连结AE、DE、DC (1)、求证:△ABE≌△CBD;(2)、若∠CAE=30°,求∠BDC的度数.22. 如图,在△ABC中,∠A=90°,∠ABC=30°,AC=3,动点D从点A出发,在AB边上以每秒1个单位的速度向点B运动,连结CD,作点A关于直线CD的对称点E,设点D运动时间为t(s).
(1)、求证:△ABE≌△CBD;(2)、若∠CAE=30°,求∠BDC的度数.22. 如图,在△ABC中,∠A=90°,∠ABC=30°,AC=3,动点D从点A出发,在AB边上以每秒1个单位的速度向点B运动,连结CD,作点A关于直线CD的对称点E,设点D运动时间为t(s).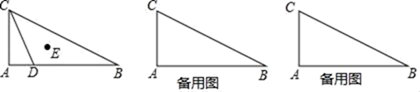 (1)、若△BDE是以BE为底的等腰三角形,求t的值;(2)、若△BDE为直角三角形,求t的值;(3)、当S△BCE≤ 时,所有满足条件的t的取值范围(所有数据请保留准确值,参考数据:tan15°=2﹣ ).23. 对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若⊙C上存在一个点M,使得MP=MC,则称点P为⊙C的“等径点”,已知点D( , ),E(0,2 ),F(﹣2,0).(1)、当⊙O的半径为1时,
(1)、若△BDE是以BE为底的等腰三角形,求t的值;(2)、若△BDE为直角三角形,求t的值;(3)、当S△BCE≤ 时,所有满足条件的t的取值范围(所有数据请保留准确值,参考数据:tan15°=2﹣ ).23. 对于平面直角坐标系xOy中的点P和⊙C,给出如下定义:若⊙C上存在一个点M,使得MP=MC,则称点P为⊙C的“等径点”,已知点D( , ),E(0,2 ),F(﹣2,0).(1)、当⊙O的半径为1时,①在点D,E,F中,⊙O的“等径点”是哪几个点;
②作直线EF,若直线EF上的点T(m,n)是⊙O的“等径点”,求m的取值范围.
(2)、过点E作EG⊥EF交x轴于点G,若△EFG各边上所有的点都是某个圆的“等径点”,求这个圆的半径r的取值范围.