广东省江门市新会区2019年中考数学一模考试试卷

试卷更新日期：2020-03-30 类型：中考模拟

进入出卷网下载

一、单选题

1. 如图，数轴上的点A，B分别对应实数a，b，下列结论正确是（　　）

A、a+b＜0 B、|a|＞|b| C、a+b＞0 D、a•b＞0

查看试题解析
2. 化简代数式 $\frac{x^{2} + x}{x - 1}$ + $\frac{1 + x}{1 - x}$ 的结果是（　　）

A、x+1 B、x﹣1 C、 $\frac{{(x + 1)}^{2}}{x - 1}$ D、 $\frac{x^{2} + 1}{x - 1}$

查看试题解析
3. 据权威统计，去年江门有80%以上的家庭年收入不低于10万元，下面一定不低于10万元的是（　　）

A、家庭年收入的平均数 B、家庭年收入的众数 C、家庭年收入的中位数 D、家庭年收入的平均数和众数

查看试题解析
4. 将点 $A (2, - 1)$ 向左平移 $3$ 个单位长度，在向上平移 $4$ 个单位长度得到点 $B$ ，则点 $B$ 的坐标是（）

A、 $(5, 3)$ B、 $(5, - 5)$ C、 $(- 1, - 5)$ D、 $(- 1, 3)$

查看试题解析
5. 关于x的一元二次方程x²﹣2x+m＝0总有实数根，则m应满足的条件是（　　）

A、m≥1 B、m≤1 C、m＝1 D、m＜1

查看试题解析
6. 我国古代数学名著《孙子算经》中记载了一道题，大意是：100匹马恰好拉了100片瓦，已知1匹大马能拉3片瓦，3匹小马能拉1片瓦，问有多少匹大马、多少匹小马？若设大马有x匹，小马有y匹，那么可列方程组为（）

A、 ${\begin{matrix} x + y = 100 \\ 3 x + 3 y = 100 \end{matrix}$ B、 ${\begin{matrix} x + y = 100 \\ x + 3 y = 100 \end{matrix}$ C、 ${\begin{matrix} x + y = 100 \\ 3 x + \frac{1}{3} y = 100 \end{matrix}$ D、 ${\begin{matrix} x + y = 100 \\ 3 x + y = 100 \end{matrix}$

查看试题解析
7. 如果三角形满足一个角是另一个角的3倍，那么我们称这个三角形为“智慧三角形”．下列各组数据中，能作为一个智慧三角形三边长的一组是（）

A、1，2，3 B、1，1， $\sqrt{2}$ C、1，1， $\sqrt{3}$ D、1，2， $\sqrt{3}$

查看试题解析
8. 如图，在Rt△ABC中，∠C＝90°，∠CAB的平分线交BC于点D，DE恰好是AB的垂直平分线，垂足为E．若BC＝6，则AB的长为（　　）

A、3 $\sqrt{3}$ B、4 $\sqrt{3}$ C、8 D、10

查看试题解析
9. 如图，正△ABC的边长为1，过点B的直线l⊥AB，且△ABC与△A′BC′关于直线l对称，D为线段BC′上一动点，则AD+CD的最小值和最大值分别是（　　）

A、2，1+2 $\sqrt{2}$ B、2，3 C、2，1+ $\sqrt{3}$ D、2，1+ $\sqrt{5}$

查看试题解析
10. 如图，P（m，m）是反比例函数y＝ $\frac{4}{x}$ 在第一象限内的图象上一点，以P为顶点作等边△PAB，使AB落在x轴上，则△POB的面积为（　　）

A、2+ $\frac{\sqrt{3}}{3}$ B、2+ $\frac{\sqrt{3}}{2}$ C、2+ $\frac{2 \sqrt{3}}{3}$ D、 $\frac{8 \sqrt{3}}{8}$

查看试题解析

二、填空题

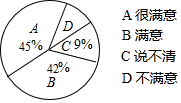
11. 李克强总理在第十三届二次全国人民代表大会作的政府工作报告中，2018年国内生产总值（GDP）总量突破90万亿元，90万亿元用科学记数法可表示为．（提示：1万亿＝1，000，000，000，000）

查看试题解析
12. 医院为了解医护人员的服务质量，随机调查了来就诊的200名病人，调查的结果如图所示．根据图中给出的信息，这200名顾客中对该医院医护人员的服务质量表示不满意的有人．

查看试题解析
13. 分解因式：4x²y³﹣4x²y²+x²y＝．

查看试题解析
14. 把函数y＝x²的图象向右平移2个单位长度，再向下平移1个单位长度，得到函数的图象．

查看试题解析
15. 在平行四边形ABCD中，∠A＝132°，在AD上取一点E，使DE＝DC，则∠ECB的度数是．

查看试题解析
16. 如图，在△ABC中，∠A＝65°，BC＝6，以BC为直径的半圆O与AB、AC分别交于点D、E，则图中由O、D、E三点所围成的扇形面积等于．（结果保留π）

查看试题解析

三、解答题

17. 计算： $\sqrt[3]{8}$ ﹣ $\frac{2}{\sqrt{3} + \sqrt{2}}$ ﹣（ $\frac{1}{2}$ ）^﹣¹+4cos30°

查看试题解析
18. 先化简，再求值： $\frac{1 - x}{1 + x}$ ÷（x﹣ $\frac{2 x}{1 + x}$ ），其中x＝ $\sqrt{2}$ +1．

查看试题解析
19. 如图，在Rt△ $A B C$ 中，∠ $A C B$ =90°．

(1)、先作∠ $A B C$ 的平分线交 $A C$ 边于点 $O$ ，再以点 $O$ 为圆心， $O C$ 为半径作⊙ $O$ （要求：尺规作图，保留作图痕迹，不写作法）；

(2)、请你判断（1）中 $A B$ 与⊙ $O$ 的位置关系，并证明你的结论．

查看试题解析
20. 在一个不透明的盒子里，装有5个分别标有数字1，2，3，4，5的小球，它们的形状、大小、质地等完全相同．雄威同学先从盒子里随机取出第一个小球，记下数字为x；不放回盒子，再由丽贤同学随机取出第二个小球，记下数字为y．

(1)、请用树状图或列表法表示出坐标（x，y）的所有可能出现的结果；

(2)、求雄威同学、丽贤同学各取一个小球所确定的点（x，y）落在反比例函数y＝ $\frac{5}{x}$ 的图象上的概率．

查看试题解析
21. 水果店进口一种高档水果，卖出每斤水果盈利（毛利润）5元，每天可卖出1000斤，经市场调査后发现，在进价不变的情况下，若每斤售价涨0.5元，每天销量将减少40斤．

(1)、若以每斤盈利9元的价钱出售，问每天能盈利多少元？

(2)、若水果店要保证每天销售这种水果的毛利润为6000元，同时又要使顾客觉得价不太贵，则每斤水果应涨价多少元？

查看试题解析
22. 已知：如图，在平行四边形ABCD中，E、F分别为边AB、CD的中点，BD是对角线，AG∥DB交CB的延长线于G．

(1)、求证：△ADE≌△CBF；

(2)、若四边形BEDF是菱形，则四边形AGBD是什么特殊四边形？并证明你的结论．

查看试题解析
23. 如图，一次函数y＝kx+b（k、b为常数，k≠0）的图象与x轴、y轴分别交于A、B两点，且与反比例函数y＝ $\frac{m}{x}$ （m为常数且m≠0）的图象在第二象限交于点C，CD⊥x轴，垂足为D，若OB＝2OA＝3OD＝6．

(1)、求一次函数与反比例函数的解析式；

(2)、求两个函数图象的另一个交点E的坐标；

(3)、请观察图象，直接写出不等式kx+b≥ $\frac{m}{x}$ 的解集．

查看试题解析
24. 如图，直线AB经过⊙O上的点C，并且OA＝OB，CA＝CB，⊙O交直线OB于E，D，连接EC，CD．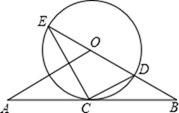

(1)、求证：直线AB是⊙O的切线；

(2)、试猜想BC，BD，BE三者之间的等量关系，并加以证明；

(3)、若tan∠CED＝ $\frac{1}{2}$ ，⊙O的半径为3，求OA的长．

查看试题解析
25. 如图，已知抛物线y＝﹣ $\frac{\sqrt{3}}{3}$ x²+bx+c与x轴交于原点O和点A（6，0），抛物线的顶点为B．

(1)、求该抛物线的解析式和顶点B的坐标；

(2)、若动点P从原点O出发，以每秒1个长度单位的速度沿线段OB运动，设点P运动的时间为t（s）．问当t为何值时，△OPA是直角三角形？

(3)、若同时有一动点M从点A出发，以2个长度单位的速度沿线段AO运动，当P、M其中一个点停止运动时另一个点也随之停止运动．设它们的运动时间为t（s），连接MP，当t为何值时，四边形ABPM的面积最小？并求此最小值．

查看试题解析