吉林省长春市2020年中考数学一模考试试卷
试卷更新日期:2020-03-30 类型:中考模拟
一、单选题
-
1. 2019的相反数是( )A、 -2019 B、2019 C、 D、2. 据统计,第15中国(长春)国际汽车博览会成交额约为6 058 000 000,6 058 000 000这个数用科学记数法表示为( )A、60.58×1010 B、6.058×1010 C、6.058×109 D、6.058×1083. 把多项式a3﹣a分解因式,下列结果正确是( )A、a(a2﹣1) B、(a+1)(a﹣1) C、a(a+1)(a﹣1) D、a(a﹣1)24. 下列几何体中,主视图和俯视图都为矩形的是( )A、
 B、
B、 C、
C、 D、
D、 5. 不等式组 的解集在数轴上表示为A、
5. 不等式组 的解集在数轴上表示为A、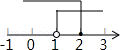 B、
B、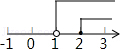 C、
C、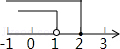 D、
D、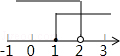 6. 一元二次方程2x2﹣4x+1=0的根的情况是( )A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根7. 如图,直线 与直线 交于点 ,关于x的不等式 的解集是( )
6. 一元二次方程2x2﹣4x+1=0的根的情况是( )A、没有实数根 B、只有一个实数根 C、有两个相等的实数根 D、有两个不相等的实数根7. 如图,直线 与直线 交于点 ,关于x的不等式 的解集是( ) A、 B、 C、 D、8. 如图,在平面直角坐标系中,过反比例函数y= (k<0,<0)的图象上一点A作AB⊥x轴于B,连结AO,过点B作BC∥AO交y轴于点C.若点A的纵坐标为4,且tan∠BCO= ,则k的值为( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,过反比例函数y= (k<0,<0)的图象上一点A作AB⊥x轴于B,连结AO,过点B作BC∥AO交y轴于点C.若点A的纵坐标为4,且tan∠BCO= ,则k的值为( ) A、 B、 C、 D、24
A、 B、 C、 D、24二、填空题
-
9. 写出一个比5大且比6小的无理数.10. 《九章算术》是中国传统数学最重要的著作,方程术是《九章算术》最高的数学成就.《九章算术》中记载:今有牛五、羊二,直金十两;牛二、羊五,直金八两.问:牛、羊各直金几何?译文:假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两.问每头牛、每只羊各值金多少?若设每头牛值金x两,每只羊值金y两,可列方程组为 .11. 如图,AB∥CD.若∠ACD=82°,∠CED=29°,则∠ABD的大小为度.
 12. 如图,海面上B、C两岛分别位于A岛的正东和正北方向,A岛与C岛之间的距离约为36海里,B岛在C岛的南偏东43°,A、B两岛之间的距离约为海里(结果精确到0.1海里)(参考数据:sin43°=0.68,cos43°=0.73,tan43°=0.93)
12. 如图,海面上B、C两岛分别位于A岛的正东和正北方向,A岛与C岛之间的距离约为36海里,B岛在C岛的南偏东43°,A、B两岛之间的距离约为海里(结果精确到0.1海里)(参考数据:sin43°=0.68,cos43°=0.73,tan43°=0.93) 13. 如图,在平面直角坐标系中,抛物线y= -1的顶点为A,直线l过点P(0,m)且平行于x轴,与抛物线交于点B和点C.若AB=AC,∠BAC=90°,则m=.
13. 如图,在平面直角坐标系中,抛物线y= -1的顶点为A,直线l过点P(0,m)且平行于x轴,与抛物线交于点B和点C.若AB=AC,∠BAC=90°,则m=. 14. 在数学课上,老师提出如下问题
14. 在数学课上,老师提出如下问题
老师说:“小华的作法符合题意”
请回答:小华第二步作图的依据是 .
三、解答题
-
15. 先化简,再求值:(x+1)2+x(x-2),其中x=- .16. 一个不透明的口袋中装有三个小球,上面分别标有数字3、4、5,这些小球除数字不同外其余均相同.(1)、从口袋中随机摸出一个小球,小球上的数字是偶数的概率是.(2)、从口袋中随机摸出一个小球,记下数字后放回,再随机摸出一个小球,记下数字,请用画树状图(或列表)的方法,求两次摸出的小球上的数字都是奇数的概率.17. 如图,在⊙O中,点C为OB的中点,点D为弦AB的中点,连结CD并延长,交过点A的切线于点E.求证:AE⊥CE.
 18. 甲、乙两名同学做中国结.已知甲每小时比乙少做6个中国结,甲做30个中国结所用的时间与乙做45个中国结所用的时间相同,求甲每小时做中国结的个数.19. 如图,E是平行四边形ABCD的边BA延长线上一点,AE=AB,连结AC、DE、CE.
18. 甲、乙两名同学做中国结.已知甲每小时比乙少做6个中国结,甲做30个中国结所用的时间与乙做45个中国结所用的时间相同,求甲每小时做中国结的个数.19. 如图,E是平行四边形ABCD的边BA延长线上一点,AE=AB,连结AC、DE、CE. (1)、求证:四边形ACDE为平行四边形.(2)、若AB=AC,AD=4,CE=6,求四边形ACDE的面积.20. 张老师计划通过步行锻炼身体,她用运动手环连续记录了6天的运动情况,并用统计表和统计图记录数据:
(1)、求证:四边形ACDE为平行四边形.(2)、若AB=AC,AD=4,CE=6,求四边形ACDE的面积.20. 张老师计划通过步行锻炼身体,她用运动手环连续记录了6天的运动情况,并用统计表和统计图记录数据:日期
4月1日
4月2日
4月3日
4月4日
4月5日
4月6日
步行数(步)
10672
4927
5543
6648
步行距离(公里)
6.8
3.1
3.4
4.3
卡路里消耗(千卡)
157
79
91
127
燃烧脂肪(克)
20
10
12
16
 (1)、请你将手环记录的4月5日和4月6日的数据(如图①)填入表格(2)、请你将条形统计图(如图②)补充完整(3)、张老师这6天平均每天步行约公里,张老师分析发现每天步行距离和消耗的卡路里近似成正比例关系,她打算每天消耗的卡路里至少达到100千卡,那么每天步行距离大约至少为公里(精确到0.1公里)21. 某校初三年级进行女子800米测试,甲、乙两名同学同时起跑,甲同学先以a米/秒的速度匀速跑,一段时间后提高速度,以 米/秒的速度匀速跑,b秒到达终点,乙同学在第60秒和第140秒时分别减慢了速度,设甲、乙两名同学所的路程为s(米),乙同学所用的时间为t(秒),s与t之间的函数图象如图所示.
(1)、请你将手环记录的4月5日和4月6日的数据(如图①)填入表格(2)、请你将条形统计图(如图②)补充完整(3)、张老师这6天平均每天步行约公里,张老师分析发现每天步行距离和消耗的卡路里近似成正比例关系,她打算每天消耗的卡路里至少达到100千卡,那么每天步行距离大约至少为公里(精确到0.1公里)21. 某校初三年级进行女子800米测试,甲、乙两名同学同时起跑,甲同学先以a米/秒的速度匀速跑,一段时间后提高速度,以 米/秒的速度匀速跑,b秒到达终点,乙同学在第60秒和第140秒时分别减慢了速度,设甲、乙两名同学所的路程为s(米),乙同学所用的时间为t(秒),s与t之间的函数图象如图所示. (1)、乙同学起跑的速度为米/秒;(2)、求a、b的值;(3)、当乙同学领先甲同学60米时,直接写出t的值是.22. (感知)如图①,点C是AB中点,CD⊥AB,P是CD上任意一点,由三角形全等的判定方法“SAS”易证△PAC≌△PBC,得到线段垂直平分线的一条性质“线段垂直平分线上的点到线段两端的距离相等”
(1)、乙同学起跑的速度为米/秒;(2)、求a、b的值;(3)、当乙同学领先甲同学60米时,直接写出t的值是.22. (感知)如图①,点C是AB中点,CD⊥AB,P是CD上任意一点,由三角形全等的判定方法“SAS”易证△PAC≌△PBC,得到线段垂直平分线的一条性质“线段垂直平分线上的点到线段两端的距离相等”
(探究)如图②,
(1)、在平面直角坐标系中,直线y=- x+1分别交x轴、y轴于点A和点B,点C是AB中点,CD⊥AB交OA于点D,连结BD,求BD的长(2)、将线段AB绕点A顺时针旋转90°得到线段AB′,请在图③网格中画出线段AB;(3)、若存在一点P,使得PA=PB′,且∠APB′≠90°,当点P的横、纵坐标均为整数时,则AP长度的最小值为 .23. 如图,在Rt△ABC中,∠ABC=90°,AB=4,BC=2.点P从点A出发,以每秒 个单位长度的速度向终点C运动,点Q从点B出发,以每秒2个单位长度的速度向终点A运动,连接PQ,将线段PQ绕点Q顺时针旋转90°得到线段QE,以PQ、QE为边作正方形PQEF.设点P运动的时间为t秒(t>0) (1)、点P到边AB的距离为(用含t的代数式表示)(2)、当PQ∥BC时,求t的值(3)、连接BE,设△BEQ的面积为S,求S与t之间的函数关系式(4)、当E、F两点中只有一个点在△ABC的内部时,直接写出t的取值范围24. 在平面直角坐标系中,已知抛物线y=x2-2mx-3m(1)、当m=1时,
(1)、点P到边AB的距离为(用含t的代数式表示)(2)、当PQ∥BC时,求t的值(3)、连接BE,设△BEQ的面积为S,求S与t之间的函数关系式(4)、当E、F两点中只有一个点在△ABC的内部时,直接写出t的取值范围24. 在平面直角坐标系中,已知抛物线y=x2-2mx-3m(1)、当m=1时,①抛物线的对称轴为直线 ,
②抛物线上一点P到x轴的距离为4,求点P的坐标
③当n≤x≤ 时,函数值y的取值范围是- ≤y≤2-n,求n的值
(2)、设抛物线y=x2-2mx-3m在2m-1≤x≤2m+1上最低点的纵坐标为y0 , 直接写出y0与m之间的函数关系式及m的取值范围.