广东省肇庆市封开县2020年中考数学一模考试试卷
试卷更新日期:2020-03-30 类型:中考模拟
一、单选题
-
1. 实数 , 在数轴上的对应点的位置如图所示,把 , ,0按照从小到大的顺序排列,正确是( )
 A、 B、 C、 D、2. 据统计,某市户籍人口约为3700000人,将3700000用科学记数法表示为( )A、 B、 C、 D、3. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、等边三角形 B、圆 C、矩形 D、平行四边形4. 下列运算中,正确是( )A、 B、 C、 D、5. 一个十字路口的交通信号灯每分钟红灯亮30s,绿灯亮25s,黄灯亮5s,当你抬头看信号灯时,是绿灯的概率是( )A、 B、 C、 D、6. 已知点(2,3)在反比例函数y= 的图象上,则该图象必过的点是( )A、 B、 C、 D、7. 一元二次方程 的根的情况为( )A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法确定8. 若 ,则 ( )A、-6 B、6 C、9 D、-99. 如图,四边形ABCD内接于⊙O,F是 上一点,且 ,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( )
A、 B、 C、 D、2. 据统计,某市户籍人口约为3700000人,将3700000用科学记数法表示为( )A、 B、 C、 D、3. 下列图形中,是中心对称图形但不是轴对称图形的是( )A、等边三角形 B、圆 C、矩形 D、平行四边形4. 下列运算中,正确是( )A、 B、 C、 D、5. 一个十字路口的交通信号灯每分钟红灯亮30s,绿灯亮25s,黄灯亮5s,当你抬头看信号灯时,是绿灯的概率是( )A、 B、 C、 D、6. 已知点(2,3)在反比例函数y= 的图象上,则该图象必过的点是( )A、 B、 C、 D、7. 一元二次方程 的根的情况为( )A、有两个相等的实数根 B、有两个不相等的实数根 C、没有实数根 D、无法确定8. 若 ,则 ( )A、-6 B、6 C、9 D、-99. 如图,四边形ABCD内接于⊙O,F是 上一点,且 ,连接CF并延长交AD的延长线于点E,连接AC.若∠ABC=105°,∠BAC=25°,则∠E的度数为( ) A、45° B、50° C、55° D、60°10. 如图,正方形 的边长为4,点 、 分别为 、 的中点,动点 从点 向点 运动,到点 时停止运动;同时,动点 从点 出发,沿 运动,点 、 的运动速度相同,设点 的运动路程为 , 的面积为 ,能大致刻画 与 的函数关系的图像是( )
A、45° B、50° C、55° D、60°10. 如图,正方形 的边长为4,点 、 分别为 、 的中点,动点 从点 向点 运动,到点 时停止运动;同时,动点 从点 出发,沿 运动,点 、 的运动速度相同,设点 的运动路程为 , 的面积为 ,能大致刻画 与 的函数关系的图像是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11.12. 分解因式: .13. 已知一个多边形的每一个内角都是 ,则这个多边形是边形.14. 在平面直角坐标系中,点 与点Q( )关于原点对称,那么 ;15. 一次函数的图象经过点 和 ,它的解析式是.16. 如图,在正方形 中, ,分别以 、 为圆心, 长为半径画弧,则图中阴影部分的面积为(结果保留 )
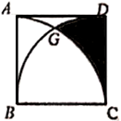 17. 一组数为: , , , , ……则第8个数为.
17. 一组数为: , , , , ……则第8个数为.三、解答题
-
18. 解方程组:19. 先化简,再求值: ,其中 .20. 如图,已知▱ABCD.
 (1)、作∠B的平分线交AD于E点。(用尺规作图法,保留作图痕迹,不要求写作法);(2)、若▱ABCD的周长为10,CD=2,求DE的长。21. 某校为研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干学生的兴趣爱好;并将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题:
(1)、作∠B的平分线交AD于E点。(用尺规作图法,保留作图痕迹,不要求写作法);(2)、若▱ABCD的周长为10,CD=2,求DE的长。21. 某校为研究学生的课余爱好情况,采取抽样调查的方法,从阅读、运动、娱乐、上网等四个方面调查了若干学生的兴趣爱好;并将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息解答下列问题: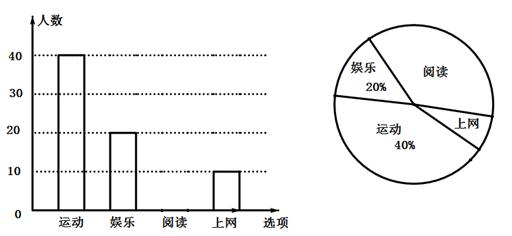 (1)、在这次研究中,一共调查了名学生;若该校共有1500名学生,估计全校爱好运动的学生共有名;(2)、补全条形统计图,并计算阅读部分圆心角是多少度;(3)、若该校九年级爱好阅读的学生有150人,估计九年级有多少学生?22. 如图,在 中, , D 是 BC 的中点, , ,若 AC=2 , CE=4 ;
(1)、在这次研究中,一共调查了名学生;若该校共有1500名学生,估计全校爱好运动的学生共有名;(2)、补全条形统计图,并计算阅读部分圆心角是多少度;(3)、若该校九年级爱好阅读的学生有150人,估计九年级有多少学生?22. 如图,在 中, , D 是 BC 的中点, , ,若 AC=2 , CE=4 ;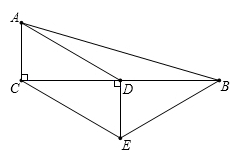 (1)、求证:四边形 是平行四边形(2)、求 的长.23. 在“双十一”购物街中,某儿童品牌玩具专卖店购进了 两种玩具,其中 类玩具的金价比 玩具的进价每个多 元.经调查发现:用 元购进 类玩具的数量与用 元购进 类玩具的数量相同.(1)、求 的进价分别是每个多少元?(2)、该玩具店共购进 了两类玩具共 个,若玩具店将每个 类玩具定价为 元出售,每个 类玩具定价 元出售,且全部售出后所获得的利润不少于 元,则该淘宝专卖店至少购进 类玩具多少个?
(1)、求证:四边形 是平行四边形(2)、求 的长.23. 在“双十一”购物街中,某儿童品牌玩具专卖店购进了 两种玩具,其中 类玩具的金价比 玩具的进价每个多 元.经调查发现:用 元购进 类玩具的数量与用 元购进 类玩具的数量相同.(1)、求 的进价分别是每个多少元?(2)、该玩具店共购进 了两类玩具共 个,若玩具店将每个 类玩具定价为 元出售,每个 类玩具定价 元出售,且全部售出后所获得的利润不少于 元,则该淘宝专卖店至少购进 类玩具多少个?

