吉林省长春市2019年中考数学三模考试试卷
试卷更新日期：2020-03-30 类型：中考模拟
一、单选题
-
1. 如图，检测4个足球，其中超过标准质量的克数记为正数，不足标准质量的克数记为负数．从轻重的角度看，最接近标准的是（ ）A、
B、
C、
D、
2. 若6﹣x＞x，则下列不等式一定成立的是（ ）A、x≥2 B、x＜3 C、x≥4 D、x≤33. 据统计，全国每小时约有510000000吨污水排入江海，510000000用科学记数法表示为（ ）A、5.1×109 B、510×106 C、5.1×106 D、5.1×1084. 如图，用量角器度量∠AOB，可以读出∠AOB的度数为（ ）
A、10° B、65° C、75° D、90°5. 如图，在菱形ABCD中，E，F分别是AC，AD的中点，若EF＝2，则菱形ABCD的周长是（ ）
A、8 B、12 C、16 D、206. 如图，某数学活动小组在吉林广播电视塔周边做数学测算活动、在C处测得最高点A的仰角为α，在D处测得最高点A的仰角为β，点C，B，D在同一条水平直线上，且吉林广播电视塔的高度AB为h（m），则CD之间的距离为（ ）
A、h•（tanα+tanβ）m B、 C、 D、7. 如图，把一张圆形纸片折叠两次后展开，图中的虚线表示折痕，则 所对圆心角的度数是（ ）
A、120° B、135° C、150° D、165°8. 如图，在平面直角坐标系中，点B在函数y＝x图象上，点A在x轴的正半轴上，等腰直角三角形BCD的顶点C在AB上，点D在函数y＝ 第一象限的图象上若△OAB与△BCD面积的差为2，则k的值为（ ）
A、8 B、4 C、2 D、1二、填空题
-
9. 因式分解：b2﹣b4＝ ．10. 比较大小： （选填“＞”“＜”或“＝”）11. 如图，在四边形ABCD中，∠BAC＝∠D，CA平分∠DCB，若AB＝3，AC＝5，BC＝7，则AD的长为 ．
12. 如图，点A，B，C，D是⊙O上的四个点，已知∠BCD＝110°，格据推断出∠BAD的度数为70°，则她判断的依据是点 ．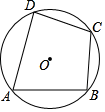
13. 如图，在Rt△ABC中，∠C＝90°，∠B＝30°，以点A为圆心，小于AC长为半径作圆弧，分别交AB，AC于M，N两点；再分别以点M，N为圆心，大于 MN长为半径作圆弧，两条圆弧交于点P，作射线AP交边BC于点D．若△ABC的面积为10，则△ACD的面积为 ．
14. 二次函数y＝x2+bx的对称轴为x＝1，若关于x的一元二次方程x2+bx﹣t＝0（为实数）在﹣1＜x＜4的范围内有解，则t的取值范围是 ．三、解答题
-
15. 先化简，再求值：3（2m+1）+2（m﹣1）2 ， 其中m是方程x2+x﹣4＝0的根．16. 小王用600元批发黄瓜和菜花共200市斤，两种菜的进价和售价如下表，若两种菜在当天全部售出，求小王当天的利润．
黄瓜
菜花
进价（元/市斤）
2.8
3.2
售价（元/市斤）
4
4.5
17. 桌面上有四张正面分别标有数字1，2，3，4的不透明卡片，它们除数字外其余全部相同，现将它们背面朝上洗匀，然后，随机翻开两张卡片求两张卡片正面所标数字之和是偶数的概率18. 如表是我国运动员在最近六届奥运会上所获奖牌总数情况：届数
金牌
银牌
铜牌
奖牌总数
26
16
22
12
50
27
28
16
15
59
28
32
17
14
63
29
51
21
28
100
30
38
27
23
88
31
26
18
26
70
数学小组分析了上面的数据，得出这六届奥运会我国奖牌总数的平均数、中位数如表所示：
统计量
平均数
中位数
数值
约为71.67
m
(1)、上表中的中位数m的值为；(2)、经过数学小组的讨论，认为由于第29届奥运会在我国北京召开，我国运动员的成绩超常，所以其数据应记为极端数据，在计算平均数时应该去掉，于是计算了另外五属奥运会上我国奖总数的平均数，这个平均数应该是(3)、根据上面提供的信息，预估我国运动员在2020年举行的第32届奥运会上将获得多少枚奖牌，并写出你的预估理由19. 问题：如果α，β都为锐角，且tanα＝ ，tanβ＝ ，求α+β的度数．
解决：
(1)、如图①，把α，β放在正方形网格中，使得∠ABD＝α，∠CBE＝β，连结AC，易证△ABC是等腰直角三角形，因此可求得α+β＝∠ABC＝ ．(2)、拓展：参考以上方法，解决下列问题：如果α，β都为锐角，当tanα＝4，tanβ＝ 时，
在图②的正方形网格中，利用已作出的锐角α，画出∠MON＝α﹣β；(3)、求出α﹣β＝°．20. 如图，在平面直角坐标系中，抛物线y＝ax2+ x+2与x轴交于点A（4，0）与y轴交于点B．点M在线段AB上，其横坐标为m，PM∥y轴，与抛物线交点为点P，PQ∥x轴，与抛物线交点为点Q
(1)、求a的值、并写出此抛物线顶点的坐标；(2)、求m为何值时，△PMQ为等腰直角三角形．21. 如图①，甲、乙两车同时从A地出发，分别匀速前往B地与C地，甲车到达B地休息一段时间后原速返回，乙车到达C地后立即返回．两车恰好同时返回A地．图②是两车各自行驶的路程y（千米）与出发时间x（时）之间的函数图象．根据图象解答下列问题：
(1)、甲车到达B地休息了时；(2)、求甲车返回A地途中y与x之间的函数关系式；(3)、当x为何值时，两车与A地的路程恰好相同．（不考虑两车同在A地的情况）22.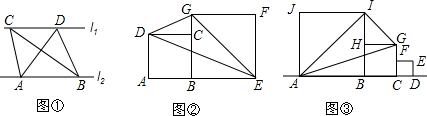
(1)、探究：如图①，直线l1∥l2 ， 点A、B在直线l1上，点C、D在直线l2上，记△ABC的面积为S1 ， △ABD的面积为S2，求证：S1＝S2 ．(2)、拓展：如图②，E为线段AB延长线上一点，BE＞AB，正方形ABCD、正方形BEFG均在直线AB同侧，求证：△DEG的面积是正方形BEFG面积的一半．(3)、应用：如图③，在一条直线上依次有点A、B、C、D，正方形ABIJ、正方形BCGH、正方形CDEF均在直线AB同侧，且点F、H分别是边CG、BI的中点，若正方形CDEF的面积为l，则△AGI的面积为 ．23. 如图，在▱ABCD中，对角线DB⊥AD，BC＝3，BD＝4．点P从点A出发，沿AB以每秒2个单位长度的速度向终点B运动（点P不与点A，B重合），点N为AP的中点，过点N作NM⊥AB交折线AD﹣DC于点M，以MN，NP为边作矩形MNPQ．设点P运动的时间为t（s）．
(1)、求线段PQ的长；（用含t的代数式表示）(2)、求点Q落在BD上时t的值；(3)、设矩形MNPQ与△ABD重叠部分图形的面积为S平方单位，当此重叠部分为四边形时，求S与t之间的函数关系式；(4)、若点D关于直线AB的对称点为点D'，点B关于直线PQ的对称点为点B'，请直接写出直线B'D'与▱ABCD各边所在直线平行或垂直的所有t的值．24. 在平面直角坐标系中，如果某点的横坐标与纵坐标的和为10，则称此点为“合适点”例如，点（1，9），（﹣2019，2029）…都是“合适点”．(1)、求函数y＝2x+1的图象上的“合适点”的坐标；(2)、求二次函数y＝x2﹣5x﹣2的图象上的两个“合适点”A，B之间线段的长；(3)、若二次函数y＝ax2+4x+c的图象上有且只有一个合适点”，其坐标为（4，6），求二次函数y＝ax2+4x+c的表达式；(4)、我们将抛物线y＝2（x﹣n）2﹣3在x轴下方的图象记为G1 ， 在x轴及x轴上方图象记为G2 ， 现将G1沿x轴向上翻折得到G3 ， 图象G2和图象G3两部分组成的记为G，当图象G上恰有两个“合适点”时，直接写出n的取值范围．