吉林省长春市汽开区2019年中考数学三模考试试卷
试卷更新日期:2020-03-30 类型:中考模拟
一、单选题
-
1. 在如图的数轴上,A,B两点表示的数分别是a,b,则a与b的大小关系是( )
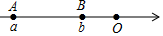 A、a>b B、a=b C、a<b D、无法确定2. 一个几何体的侧面展开图如图所示,则该几何体的底面是( )
A、a>b B、a=b C、a<b D、无法确定2. 一个几何体的侧面展开图如图所示,则该几何体的底面是( )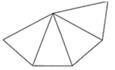 A、
A、 B、
B、 C、
C、 D、
D、 3. 若x= ﹣4,则x的取值范围是( )A、2<x<3 B、3<x<4 C、4<x<5 D、5<x<64. 关于x的不等式组 的解集为x<2,那么a的取值范围为( )A、a=2 B、a>2 C、a<2 D、a≥25. 如图,点A、B、C、D、O都在方格纸的格点上,若△COD是由△AOB绕点O按逆时针方向旋转而得,则旋转的角度为( )
3. 若x= ﹣4,则x的取值范围是( )A、2<x<3 B、3<x<4 C、4<x<5 D、5<x<64. 关于x的不等式组 的解集为x<2,那么a的取值范围为( )A、a=2 B、a>2 C、a<2 D、a≥25. 如图,点A、B、C、D、O都在方格纸的格点上,若△COD是由△AOB绕点O按逆时针方向旋转而得,则旋转的角度为( )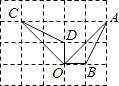 A、30° B、45° C、90° D、135°6. 如图,四边形 是半圆的内接四边形, 是直径, .若 ,则 的度数等于( )
A、30° B、45° C、90° D、135°6. 如图,四边形 是半圆的内接四边形, 是直径, .若 ,则 的度数等于( )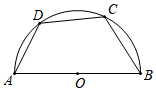 A、 B、 C、 D、7. 我国古代数学著作《九章算术》中有一道阐述“盈不足术”的问题,译文为:“现有几个人共同购买一个物品,每人出8元,则多3元:每人出7元,则差4元,问这个物品的价格是多少元?”设该商品的价格是x元,共同购买该物品的有y人,则正确方程组是( )A、 B、 C、 D、8. 如图,菱形OABC,A点的坐标为(5,0),对角线OB、AC相交于D点,双曲线y= (x>0)经过D点,交BC的延长线于E点,交AB于F点,连接OF交AC于M,且OB•AC=40.有下列四个结论:①k=8;②CE=1;③AC+OB=6 ;④S△AFM:S△AOM=1:3.其中正确结论是( )
A、 B、 C、 D、7. 我国古代数学著作《九章算术》中有一道阐述“盈不足术”的问题,译文为:“现有几个人共同购买一个物品,每人出8元,则多3元:每人出7元,则差4元,问这个物品的价格是多少元?”设该商品的价格是x元,共同购买该物品的有y人,则正确方程组是( )A、 B、 C、 D、8. 如图,菱形OABC,A点的坐标为(5,0),对角线OB、AC相交于D点,双曲线y= (x>0)经过D点,交BC的延长线于E点,交AB于F点,连接OF交AC于M,且OB•AC=40.有下列四个结论:①k=8;②CE=1;③AC+OB=6 ;④S△AFM:S△AOM=1:3.其中正确结论是( )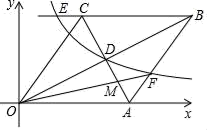 A、①② B、①③ C、①②③ D、①②③④
A、①② B、①③ C、①②③ D、①②③④二、填空题
-
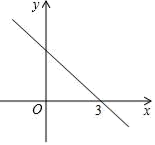
9. ﹣1的绝对值是 .10. 分解因式:x3﹣x= .11. 如图,已知一次函数y=kx+b的图象经过点(3,0),则当函数值y小于0时,自变量x的取值范围是 .
 12. 如图所示,在 中, , 是斜边 上的中线, 分别为 的中点,若 ,则 .
12. 如图所示,在 中, , 是斜边 上的中线, 分别为 的中点,若 ,则 . 13. 在△ABC中,分别以点A和点B为圆心,大于 AB的长为半径画弧,两弧相交于M,N,作直线MN,交BC于点D,连接AD.如果BC=5,CD=2,那么AD= .
13. 在△ABC中,分别以点A和点B为圆心,大于 AB的长为半径画弧,两弧相交于M,N,作直线MN,交BC于点D,连接AD.如果BC=5,CD=2,那么AD= .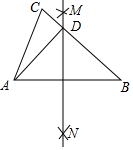 14. 抛物线y= x2的开口方向 , 对称轴是 , 顶点是 , 当x<0时,y随x的增大而;当x>0时,y随x的增大而;当x=0时,y有最值是 .
14. 抛物线y= x2的开口方向 , 对称轴是 , 顶点是 , 当x<0时,y随x的增大而;当x>0时,y随x的增大而;当x=0时,y有最值是 .三、解答题
-
15. 先化简再求值: ÷( ﹣1),其中x= .16. 如图是一副扑克牌中的三张牌,将它们正面向下洗均匀,甲同学从中随机抽取一张牌后放回,乙同学再从中随机抽取一张牌,用树状图(或列表)的方法,求抽出的两张牌中,牌面上的数字都是偶数的概率.
 17. 如图,矩形ABCD中,对角线AC的垂直平分线MN与AD相交于点M,与BC相交于点N,连接AN,CM.求证:四边形AMCN是菱形.
17. 如图,矩形ABCD中,对角线AC的垂直平分线MN与AD相交于点M,与BC相交于点N,连接AN,CM.求证:四边形AMCN是菱形. 18. 在一次数学综合实践活动中,小明计划测量城门大楼的高度,在点B处测得楼顶A的仰角为22°,他正对着城楼前进21米到达C处,再登上3米高的楼台D处,并测得此时楼顶A的仰角为45°.
18. 在一次数学综合实践活动中,小明计划测量城门大楼的高度,在点B处测得楼顶A的仰角为22°,他正对着城楼前进21米到达C处,再登上3米高的楼台D处,并测得此时楼顶A的仰角为45°.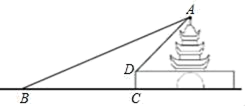 (1)、求城门大楼的高度;(2)、每逢重大节日,城门大楼管理处都要在A,B之间拉上绳子,并在绳子上挂一些彩旗,请你求出A,B之间所挂彩旗的长度(结果保留整数).(参考数据:sin22°≈ ,cos22°≈ ,tan22°≈ )19. 如图,BC是半⊙O的直径,A是⊙O上一点,过点的切线交CB的延长线于点P,过点B的切线交CA的延长线于点E,AP与BE相交于点F.
(1)、求城门大楼的高度;(2)、每逢重大节日,城门大楼管理处都要在A,B之间拉上绳子,并在绳子上挂一些彩旗,请你求出A,B之间所挂彩旗的长度(结果保留整数).(参考数据:sin22°≈ ,cos22°≈ ,tan22°≈ )19. 如图,BC是半⊙O的直径,A是⊙O上一点,过点的切线交CB的延长线于点P,过点B的切线交CA的延长线于点E,AP与BE相交于点F.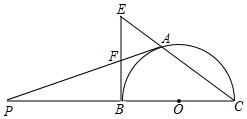 (1)、求证:BF=EF;(2)、若AF= ,半⊙O的半径为2,求PA的长度.20. 调查作业:了解你所住小区家庭3月份用气量情况
(1)、求证:BF=EF;(2)、若AF= ,半⊙O的半径为2,求PA的长度.20. 调查作业:了解你所住小区家庭3月份用气量情况小天、小东和小芸三位同学住在同一小区,该小区共有300户家庭,每户家庭人数在2~5之间,这300户家庭的平均人数约为3.3.
小天、小东、小芸各自对该小区家庭3月份用气量情况进行了抽样裯查,将收集的数据进行了整理,绘制的统计表分别为表1、表2和表3.
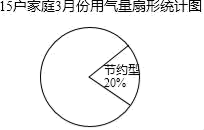
表1抽样调查小区4户家庭3月份用气量统计表(单位:m3)
家庭人数
2
3
4
5
用气量
14
19
21
26
表2抽样调查小区15户家庭3月份用气量统计表(单位:m3)
家庭人数
2
2
2
3
3
3
3
3
3
3
3
3
3
4
用气量
10
11
15
13
14
15
15
17
17
18
18
18
20
22
表3抽样调查小区15户家庭3月份用气量统计表(单位:m3)
家庭人数
2
2
2
3
3
3
3
3
3
4
4
4
4
5
5
用气量
10
12
13
14
17
17
18
20
20
21
22
26
31
28
31
根据以|材料回答问题:
(1)、小天、小东和小芸三人中,哪位同学抽样调查的数据能较好地反映出该小区家庭3月份用气量情况?请简要说明其他两位同学抽样调查的不足之处.(2)、在表3中,调查的15个家庭中使用气量的中位数是m3 , 众数是m3 .(3)、小东将表2中的数据按用气量x(m3)大小分为三类.①节约型:10≤x≤13,②适中型:14≤x≤17,③偏高型:18≤x≤22,并绘制成如图扇形统讣图,请帮助他将扇形图补充完整.
(4)、小芸算出表3中3月份平均每人的用气量为6m3 , 请估计该小区3月份的总用气量.21. 在一条笔直的公路上有A、B两地.甲、乙两人同时出发,甲骑电动车从A地到B地,中途出现故障后停车维修,修好车后以原速继续行驶到B地;乙骑摩托车从B地到A地,到达A地后立即按原原速返回,结果两人同时到B地.如图是甲、乙两人与B地的距离y(km)与乙行驶时间x(h)之间的函数图象。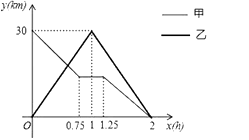 (1)、A、B两地间的距离为km;(2)、求乙与B地的距离y(km)与乙行驶时间x(h)之间的函数关系式;(3)、求甲、乙第一次相遇的时间;(4)、若两人之间的距离不超过10km时,能够用无线对讲机保持联系,请求出乙在行进中能用无线对讲机与甲保持联系的x取值范围。22. 如图,已知直线y=﹣ x+3与x轴、y轴分别相交于点A、B,再将△A0B沿直钱CD折叠,使点A与点B重合.折痕CD与x轴交于点C,与AB交于点D.
(1)、A、B两地间的距离为km;(2)、求乙与B地的距离y(km)与乙行驶时间x(h)之间的函数关系式;(3)、求甲、乙第一次相遇的时间;(4)、若两人之间的距离不超过10km时,能够用无线对讲机保持联系,请求出乙在行进中能用无线对讲机与甲保持联系的x取值范围。22. 如图,已知直线y=﹣ x+3与x轴、y轴分别相交于点A、B,再将△A0B沿直钱CD折叠,使点A与点B重合.折痕CD与x轴交于点C,与AB交于点D.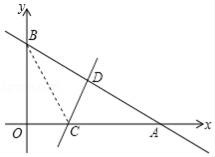 (1)、点A的坐标为;点B的坐标为;(2)、求OC的长度,并求出此时直线BC的表达式;(3)、直线BC上是否存在一点M,使得△ABM的面积与△ABO的面积相等?若存在,请直接写出点M的坐标;若不存在,请说明理由.23. 如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)、点A的坐标为;点B的坐标为;(2)、求OC的长度,并求出此时直线BC的表达式;(3)、直线BC上是否存在一点M,使得△ABM的面积与△ABO的面积相等?若存在,请直接写出点M的坐标;若不存在,请说明理由.23. 如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.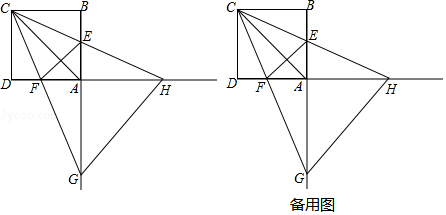 (1)、填空:∠AHC∠ACG;(填“>”或“<”或“=”)(2)、线段AC,AG,AH什么关系?请说明理由;(3)、设AE=m,
(1)、填空:∠AHC∠ACG;(填“>”或“<”或“=”)(2)、线段AC,AG,AH什么关系?请说明理由;(3)、设AE=m,①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.
24. 如图,已知抛物线 的顶点为 ,与 轴相交于点 ,对称轴为直线 ,点 是线段 的中点.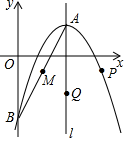 (1)、求抛物线的表达式;(2)、写出点 的坐标并求直线 的表达式;(3)、设动点 , 分别在抛物线和对称轴l上,当以 , , , 为顶点的四边形是平行四边形时,求 , 两点的坐标.
(1)、求抛物线的表达式;(2)、写出点 的坐标并求直线 的表达式;(3)、设动点 , 分别在抛物线和对称轴l上,当以 , , , 为顶点的四边形是平行四边形时,求 , 两点的坐标.