吉林省长春市净月高新区2019年中考数学模拟考试试卷

试卷更新日期：2020-03-30 类型：中考模拟

进入出卷网下载

一、单选题

1. $- 2$ 的相反数是（）

A、 $- 2$ B、2 C、 $\frac{1}{2}$ D、 $- \frac{1}{2}$

查看试题解析
2. 今年清明小长假期问，长春净月某景区接待游客约为51700人次，数字51700用科学记数法表示为（　　）

A、51.7×10³ B、5.17×10⁴ C、5.17×10⁵ D、0.517×10⁵

查看试题解析
3. 如图所示的正六棱柱的主视图是（）

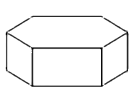A、 B、 C、 D、

查看试题解析
4. 不等式3x﹣3≤0解集在数轴上表示正确是（　　）

A、 B、 C、 D、

查看试题解析
5. 如图，AE∥DB，∠1＝85°，∠2＝28°，则∠C的度数为（　　）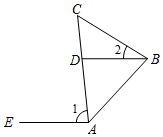

A、55° B、56° C、57° D、60°

查看试题解析
6. 如图，要测量河两相对的两点P、A之间的距离，可以在AP的垂线PB上取点C，测得PC＝100米，用测角仪测得∠ACP＝40°，则AP的长为（　　）

A、100sin40°米 B、100tan40°米 C、 $\frac{100}{\sin 40^{°}}$ 米 D、 $\frac{100}{\tan 40^{°}}$ 米

查看试题解析
7. 如图，O为圆心， $AB$ 是直径， $C$ 是半圆上的点， $D$ 是 $\overset{⌢}{A C}$ 上的点.若 $∠ BOC = 40^{\circ}$ ，则 $∠ D$ 的大小为（）

A、 $110^{\circ}$ B、 $120^{\circ}$ C、 $130^{\circ}$ D、 $140^{\circ}$

查看试题解析
8. 如图，在平面直角坐标系中，Rt△ABC的顶点A、B的坐标分别为（﹣1，1）、（3，0），直角顶点C在x轴上，在△ADE中，∠E＝90°，点D在第三象限的双曲线y＝ $\frac{k}{x}$ 上，且边AE经过点C．若AB＝AD，∠BAD＝90°，则k的值为（　　）

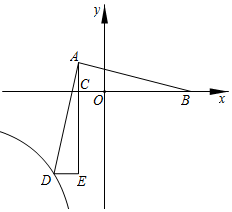A、3 B、4 C、﹣6 D、6

查看试题解析

二、填空题

9. 分解因式： $a b^{3} - a b$ = ．

查看试题解析
10. 一元二次方程2x²﹣4x+1＝0实数根（填“有”或“无”）

查看试题解析
11. 我国古代数学著作《孙子算经》中有“鸡兔同笼”问题：“今有鸡兔同笼，上有三十五头，下有八十足．问鸡兔各几何？”若设鸡有x只，兔有y只，请将题中数量关系用二元一次方程组列出得．

查看试题解析
12. 如图，在△ABC中，∠ACB=90°.按以下步骤作图，分别以点A和点B为圆心，大于 $\frac{1}{2} AB$ 的长为半径作圆弧，两弧交于点E和点F；作直线EF交AB于点D；连结CD，若AC=8，BC=6，则CD的长为.

查看试题解析
13. 如图，已知双曲线 $y = \frac{k}{x}$ （k＜0）经过直角三角形OAB斜边OA的中点D，且与直角边AB相交于点C．若点A的坐标为（﹣6，4），则△AOC的面积为．

查看试题解析
14. 在平面直角坐标系中，将二次函数y＝﹣x²+x+6在x轴上方的图象沿x轴翻折到x轴下方，图象的其余部分不变，将这个新函数的图象记为G（如图所示）．当直线y＝m与图象G有4个交点时，则m的取值范围是．

查看试题解析

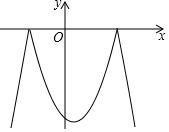
三、解答题

15. 先化简，再求值：（ $\frac{1}{x + 1}$ ﹣1）÷ $\frac{x}{x^{2} - 1}$ ，其中x＝2

查看试题解析
16. 某校期末评选出四名“优秀课代表”，其中有2名男生和2名女生，若从他们中任选2人作为代表发言，请用画树状图（或列表）的方法，求恰好选中1男1女的概率．

查看试题解析
17. 用A、B两种机器人搬运大米，A型机器人比B型机器人每小时多搬运20袋大米，A型机器人搬运700袋大米与B型机器人搬运500袋大米所用时间相等．求A、B型机器人每小时分别搬运多少袋大米．

查看试题解析
18. 如图，在菱形ABCD中，对角线AC与BD交于点O．过点C作BD的平行线，过点D作AC的平行线，两直线相交于点E．

(1)、求证：四边形OCED是矩形；

(2)、若CE＝2，DE＝3，求菱形ABCD的面积．

查看试题解析
19. 如图，线段AB经过圆心O，交⊙O于点A、C，点D为⊙O上一点，连结AD、OD、BD，∠A＝∠B＝30°．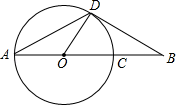

(1)、求证：BD是⊙O的切线．

(2)、若OA＝5，求OA、OD与AD围成的扇形的面积．

查看试题解析

20. 某校学生会为了解本校学生每天体育锻炼所用时间情况，采用问卷的方式对一部分学生进行调查确定调查对象时，大家提出以下几种方案：（A）对各班体育委员进行调査；（B）对某班的全体学生进行调查；（C）从全校每班随机抽5名学生进行调查在问卷调查时，每位被调查的学都选择了问卷中适合自己的十个时间段，学生会将收集到的数据整理后续制成如下的统计表：

被调查的学生每天体育锻炼所用时间统计表

组别	时间x（小时）	频数
一	0≤x≤0.5	15
二	0.6＜x≤1	27
三	1＜x≤1.5	38
四	1.5＜x≤2	13
五	x＞2	7

(1)、为了使收集到的数据具有代表性，学生会在确定调查对象时选择了方案（填A、B或C）；

(2)、被调查的学生每天体育锻炼所用时间的中位数落在组；

(3)、根据以上统计结果，估计该校900名学生中每天体育锻炼时间不超过0.5小时的人数，并根据你计算的结果提出一条合理化建议．

查看试题解析

21. 一辆轿车从甲地驶往乙地，到达乙地后立即返回甲地，速度是原来的1.5倍，往返共用t小时.一辆货车同时从甲地驶往乙地，到达乙地后停止.两车同时出发，匀速行驶，设轿车行驶的时间为x（h），两车离开甲地的距离为y（km），两车行驶过程中y与x之间的函数图象如图所示.

(1)、轿车从乙地返回甲地的速度为km/t，t=h ；

(2)、求轿车从乙地返回甲地时y与x之间的函数关系式；

(3)、当轿车从甲地返回乙地的途中与货车相遇时，求相遇处到甲地的距离.

查看试题解析
22. 图①、图②、图③均为方形网格，每个小正方形的顶点称为格点，每个小正方形的边长均为1．

（探究）在图①中，点A、B、C、D均为格点．证明：BD平分∠ABC．

（应用）在图②、图③中，点M、O、N均为格点．

(1)、利用（探究）的方法，在图②、图③中分别找到一个格点P，使OP平分∠MON．要求：图②、图③中所画的图形不相同，保留画图痕迹．

(2)、cos∠MOP的值为．

查看试题解析
23. 如图，在矩形ABCD中，AB＝6 $\sqrt{5}$ ，BC＝3 $\sqrt{5}$ 动点P从点A出发，沿AC以每秒4个单位长度的速度向终点C运动．过点P（不与点A、C重合）作EF⊥AC，交AB或BC于点E，交AD或DC于点F，以EF为边向右作正方形EFGH设点P的运动时间为t秒．

(1)、①AC＝． ②当点F在AD上时，用含t的代数式直接表示线段PF的长．

(2)、当点F与点D重合时，求t的值．

(3)、设方形EFGH的周长为l，求l与t之间的函数关系式．

(4)、直接写出对角线AC所在的直线将正方形EFGH分成两部分图形的面积比为1：2时t的值．

查看试题解析
24. 在平面直角坐标系中，对于点P（x，y）和Q（x，y′），给出如下定义：如果y′＝ ${\begin{array}{l} y (x \geq 0) \\ - y (x < 0) \end{array}$ ，那么称点Q为点P的“伴随点”．

例如：点（5，6）的“伴随点”为点（5，6）；点（﹣5，6）的“伴随点”为点（﹣5，﹣6）．

(1)、直接写出点A（2，1）的“伴随点”A′的坐标．

(2)、点B（m，m+1）在函数y＝kx+3的图象上，若其“伴随点”B′的纵坐标为2，求函数y＝kx+3的解析式．

(3)、点C、D在函数y＝﹣x²+4的图象上，且点C、D关于y轴对称，点D的“伴随点”为D′．若点C在第一象限，且CD＝DD′，求此时“伴随点”D′的横坐标．

(4)、点E在函数y＝﹣x²+n（﹣1≤x≤2）的图象上，若其“伴随点”E′的纵坐标y′的最大值为m（1≤m≤3），直接写出实数n的取值范围．

查看试题解析