吉林省长春市朝阳区2019年中考数学二模考试试卷
试卷更新日期:2020-03-30 类型:中考模拟
一、单选题
-
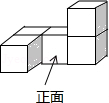
1. ﹣2的绝对值是( )A、2 B、 C、 D、2. 近年来,国家重视精准扶贫,收效显著.据统计约有65 000 000人脱贫,把65 000 000用科学记数法表示,正确是( )A、0.65×108 B、6.5×107 C、6.5×108 D、65×1063. 如图是一个由5个完全相同的小正方体组成的立体图形,它的俯视图是( )
 A、
A、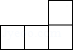 B、
B、 C、
C、 D、
D、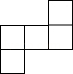 4. 不等式组 的解在数轴上表示为( )A、
4. 不等式组 的解在数轴上表示为( )A、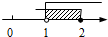 B、
B、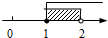 C、
C、 D、
D、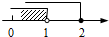 5. 如图,直线a∥b,将一个直角三角尺按如图所示的位置摆放,若∠1=52°,则∠2的度数为( )
5. 如图,直线a∥b,将一个直角三角尺按如图所示的位置摆放,若∠1=52°,则∠2的度数为( )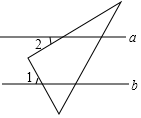 A、38° B、52° C、48° D、62°6. 关于一元二次方程x2﹣4x+4=0根的情况,下列判断正确是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、有且只有一个实数根 D、没有实数根7. 中国古代在利用“计里画方”(比例缩放和直角坐标网格体系)的方法制作地图时,会利用测杆、水准仪和照板来测量距离.在如图所示的测量距离AB的示意图中,记照板“内芯”的高度为EF,观测者的眼睛(图中用点C表示)与BF在同一水平线上,则下列结论中,正确是( )
A、38° B、52° C、48° D、62°6. 关于一元二次方程x2﹣4x+4=0根的情况,下列判断正确是( )A、有两个不相等的实数根 B、有两个相等的实数根 C、有且只有一个实数根 D、没有实数根7. 中国古代在利用“计里画方”(比例缩放和直角坐标网格体系)的方法制作地图时,会利用测杆、水准仪和照板来测量距离.在如图所示的测量距离AB的示意图中,记照板“内芯”的高度为EF,观测者的眼睛(图中用点C表示)与BF在同一水平线上,则下列结论中,正确是( )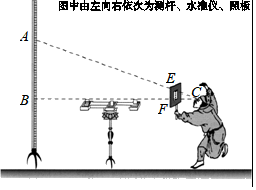 A、 B、 C、 D、8. 如图,在平面直角坐标系中,矩形ABCD的对角线AC经过坐标原点O,矩形的边分别平行于坐标轴,点B在函数 (k≠0,x>0)的图象上,点D的坐标为(﹣4,1),则k的值为( )
A、 B、 C、 D、8. 如图,在平面直角坐标系中,矩形ABCD的对角线AC经过坐标原点O,矩形的边分别平行于坐标轴,点B在函数 (k≠0,x>0)的图象上,点D的坐标为(﹣4,1),则k的值为( )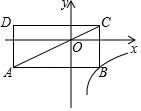 A、 B、 C、4 D、﹣4
A、 B、 C、4 D、﹣4二、填空题
-
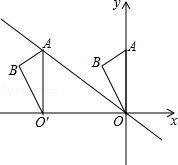
9. 比较大小: 3.10. 计算:(m5)4= .11. 如图,在平面直角坐标系中,点A的坐标为(0,6),将△OAB沿x轴向左平移得到△O′A′B′,点A的对应点A′落在直线y=﹣ x上,则点B与其对应点B′间的距离为 .
 12. 在△ABC中,分别以点A和点B为圆心,大于 AB的长为半径画弧,两弧相交于M,N,作直线MN,交BC于点D,连接AD.如果BC=5,CD=2,那么AD= .
12. 在△ABC中,分别以点A和点B为圆心,大于 AB的长为半径画弧,两弧相交于M,N,作直线MN,交BC于点D,连接AD.如果BC=5,CD=2,那么AD= .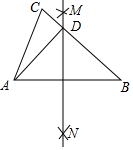 13. 如图,在△PAB中,PA=PB,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为
13. 如图,在△PAB中,PA=PB,M、N、K分别是PA,PB,AB上的点,且AM=BK,BN=AK.若∠MKN=40°,则∠P的度数为 14. 如图,在平面直角坐标系中,抛物线y=ax2﹣2ax+3(a为常数且a≠0)与y轴交于点人过点A作AC∥x轴交抛物线于点C,以AC为对角线作菱形ABCD,若菱形的顶点B恰好落在x轴上,则菱形ABCD的面积为 .
14. 如图,在平面直角坐标系中,抛物线y=ax2﹣2ax+3(a为常数且a≠0)与y轴交于点人过点A作AC∥x轴交抛物线于点C,以AC为对角线作菱形ABCD,若菱形的顶点B恰好落在x轴上,则菱形ABCD的面积为 .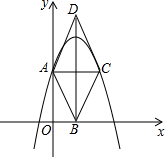
三、解答题
-
15. 某学生在化简求值: ,其中x= 时出现不符合题意,解答过程如下,
原式= (第一步)
= (第二步)
= (第三步)
当x= 是,原式= (第四步)
(1)、该学生解答过程从第步开始出错的,其不符合题意原因是 .(2)、写出此题的符合题意解答过程.16. 如图,A、B两个转盘分别被平均分成三个、四个扇形,分别转动A盘、B盘各一次.转动过程中,指针保持不动,如果指针恰好指在分割线上,则重转一次,直到指针指向一个数字所在的区域为止.请用列表或画树状图的方法,求两个转盘停止后指针所指区域内的数字之和小于6的概率.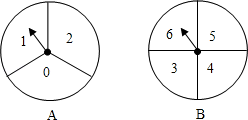 17. 如图,矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD.
17. 如图,矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD.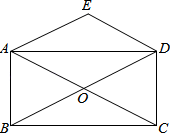 (1)、求证:四边形AODE是菱形;(2)、若将题设中“矩形ABCD”这一条件改为“菱形ABCD”,其余条件不变,则四边形AODE的形状是什么?不必说明理由.18. 2019长春国际马拉松于5月26日上午在长春体育中心鸣枪开跑.某公司为赛事赞助了5000瓶矿泉水,计划以后每年逐年增加,到2021年达到7200瓶,若该公司每年赞助矿泉水数量增加的百分率相同.(1)、求平均每年增加的百分率;(2)、假设2022年该公司赞助矿泉水增加的百分率与前两年相同,请你预测2022年该公司赞助的矿泉水的数量.19. 如图,AB是⊙O的直径,点C在⊙O上,过点C的切线交AB的延长线于点D,∠ACD=120°.
(1)、求证:四边形AODE是菱形;(2)、若将题设中“矩形ABCD”这一条件改为“菱形ABCD”,其余条件不变,则四边形AODE的形状是什么?不必说明理由.18. 2019长春国际马拉松于5月26日上午在长春体育中心鸣枪开跑.某公司为赛事赞助了5000瓶矿泉水,计划以后每年逐年增加,到2021年达到7200瓶,若该公司每年赞助矿泉水数量增加的百分率相同.(1)、求平均每年增加的百分率;(2)、假设2022年该公司赞助矿泉水增加的百分率与前两年相同,请你预测2022年该公司赞助的矿泉水的数量.19. 如图,AB是⊙O的直径,点C在⊙O上,过点C的切线交AB的延长线于点D,∠ACD=120°.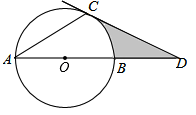 (1)、求证:AC=CD;(2)、若⊙O的半径为2,求图中阴影部分的面积.20. 中华文化历史悠久,包罗万象.某校为了加强学生对中华传统文化的认识和理解,营造校园文化氛围,举办了“弘扬中华传统文化,做新时代的中学生”的知识竞赛.以下是从七年、八年两个年级随机抽取20名同学的测试成绩进行调查分析,成绩如下:(1)、根据上面的数据,将下列表格补充完整,整理、描述数据:
(1)、求证:AC=CD;(2)、若⊙O的半径为2,求图中阴影部分的面积.20. 中华文化历史悠久,包罗万象.某校为了加强学生对中华传统文化的认识和理解,营造校园文化氛围,举办了“弘扬中华传统文化,做新时代的中学生”的知识竞赛.以下是从七年、八年两个年级随机抽取20名同学的测试成绩进行调查分析,成绩如下:(1)、根据上面的数据,将下列表格补充完整,整理、描述数据:
50≤x≤59
60≤x≤69
70≤x≤79
80≤x≤89
90≤x≤100
七年
1
2
6
八年
0
1
10
1
8
(说明:成绩90分及以上为优秀,60分以下为不合格)分析数据:
年级
平均数
中位数
众数
七年
84
88.5
八年
84.2
74
(2)、为调动学生学习传统文化的积极性,七年级根据学生的成绩制定了奖励标准,凡达到或超过这个标准的学生将获得奖励.如果想让一半左右的学生能获奖,应根据来确定奖励标准比较合适.(填“平均数”、“众数”或“中位数”);(3)、若八年级有800名学生,试估计八年级学生成绩优秀的人数; 21. 李明驾车以100千米/小时的速度从甲地匀速开往乙地,行驶到服务区休息了一段时间后以另一速度继续匀速行驶,直至到达乙地.李明与乙地的距离y(千米)与时间x(小时)之间的函数关系图象如图所示.
21. 李明驾车以100千米/小时的速度从甲地匀速开往乙地,行驶到服务区休息了一段时间后以另一速度继续匀速行驶,直至到达乙地.李明与乙地的距离y(千米)与时间x(小时)之间的函数关系图象如图所示.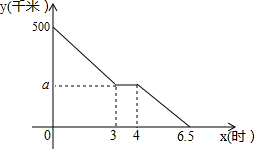 (1)、求a的值;(2)、求李明从服务区到乙地y与x之间的函数关系式;(3)、求x=5时李明驾车行驶的路程.22.
(1)、求a的值;(2)、求李明从服务区到乙地y与x之间的函数关系式;(3)、求x=5时李明驾车行驶的路程.22.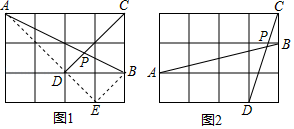
(1)、(问题背景)
如图1,在边长为1的正方形网格中,连结格点A、B和C、D,AB和CD相交于点P,求tan∠CPB的值.小马同学是这样解决的:连结格点B、E可得BE∥CD,则∠ABE=∠CPB,连结AE,那么∠CPB就变换到Rt△ABE中.则tan∠CPB的值为 .
(2)、(探索延伸)如图2,在边长为1的正方形网格中,AB和CD相交于点P,求sin∠APD的值.
23. 如图,在菱形ABCD中,对角线AC、BD相交于点O,AB=4,∠DAB=120°,动点P从点A出发,以每秒2个单位的速度沿AC向终点C运动.过P作PE⊥AB交AB于点E,作PF⊥AD交AD于点F,设四边形AEPF与△ABD的重叠部分的面积为S,点P的运动时间为t.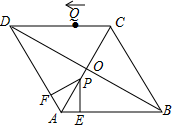 (1)、用含t的代数式表示线段BE的长;(2)、当点P与点O重合时,求t的值;(3)、求S与t之间的函数关系式;(4)、在点P出发的同时,有一点Q从点C出发,以每秒6个单位的速度沿折线C﹣D﹣A﹣B运动,设点Q关于AC的对称点是Q',直接写出PQ'与菱形ABCD的边垂直时t的值.24. 如图,在平面直角坐标系中,A(1,1),过A作线段AB∥y轴(B在A下方),以AB为边向右作正方形ABCD.设点B的纵坐标为m,二次函数y=ax2﹣4ax的图象的顶点为E.
(1)、用含t的代数式表示线段BE的长;(2)、当点P与点O重合时,求t的值;(3)、求S与t之间的函数关系式;(4)、在点P出发的同时,有一点Q从点C出发,以每秒6个单位的速度沿折线C﹣D﹣A﹣B运动,设点Q关于AC的对称点是Q',直接写出PQ'与菱形ABCD的边垂直时t的值.24. 如图,在平面直角坐标系中,A(1,1),过A作线段AB∥y轴(B在A下方),以AB为边向右作正方形ABCD.设点B的纵坐标为m,二次函数y=ax2﹣4ax的图象的顶点为E.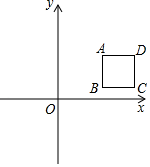 (1)、AB= . (用含m的代数式表示);(2)、当点A恰好在二次函数y=ax2﹣4ax的图象上时,求二次函数y=ax2﹣4ax的关系式.(3)、当点E恰为线段BC的中点时,求经过点D的反比例函数的关系式;(4)、若a=m+1,当二次函数y=ax2﹣4ax的图象恰与正方形ABCD有三个交点且二次函数顶点E不位于直线BC下方时,直接写出m的值.
(1)、AB= . (用含m的代数式表示);(2)、当点A恰好在二次函数y=ax2﹣4ax的图象上时,求二次函数y=ax2﹣4ax的关系式.(3)、当点E恰为线段BC的中点时,求经过点D的反比例函数的关系式;(4)、若a=m+1,当二次函数y=ax2﹣4ax的图象恰与正方形ABCD有三个交点且二次函数顶点E不位于直线BC下方时,直接写出m的值.