广东省广州市黄埔区2019年中考数学一模考试试卷

试卷更新日期：2020-03-30 类型：中考模拟

进入出卷网下载

一、单选题

1. cos30°的值是（）

A、 $\frac{\sqrt{2}}{2}$ B、 $\frac{\sqrt{3}}{3}$ C、 $\frac{1}{2}$ D、 $\frac{\sqrt{3}}{2}$

查看试题解析
2. 一个几何体的三视图如图所示，这个几何体是（）

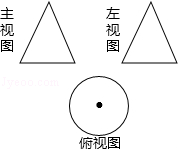A、圆锥 B、圆柱 C、球 D、三棱柱

查看试题解析
3. 下列四个等式，正确是（）

A、 $3 a^{3} \cdot 2 a^{2} = 6 a^{6}$ B、 $3 x^{2} \cdot 4 x^{2} = 12 x^{2}$ C、 $2 x^{2} \cdot 3 x^{2} = 6 x^{4}$ D、 $5 y^{3} \cdot 3 y^{5} = 15 y^{15}$

查看试题解析
4. 据统计，某住宅楼30户居民五月份最后一周每天实行垃圾分类的户数依次是：27，30，29，25，26，28，29，那么这组数据的中位数和众数分别是（）

A、25和30 B、25和29 C、28和30 D、28和29

查看试题解析
5. 下列对二次函数 $y = x^{2} + x$ 的图象的描述，正确是（）

A、对称轴是y轴 B、开口向下 C、经过原点 D、顶点在y轴右侧

查看试题解析
6. 某校春季运动会比赛中，八年级（1）班、（5）班的竞技实力相当，关于比赛结果，
甲同学说：（1）班与（5）班得分比为6 5；乙同学说：（1）班得分比（5）班得分的2倍少（）

40分．若设（1）班得x分，（5）班得y分，根据题意所列的方程组应为

A、 ${\begin{cases} \end{cases} \begin{matrix} 6 x = 5 y \\ x = 2 y - 40 \end{matrix}$ B、 ${\begin{cases} \end{cases} \begin{matrix} 6 x = 5 y \\ x = 2 y + 40 \end{matrix}$ C、 ${\begin{cases} \end{cases} \begin{matrix} 5 x = 6 y \\ x = 2 y + 40 \end{matrix}$ D、 ${\begin{cases} \end{cases} \begin{matrix} 5 x = 6 y \\ x = 2 y - 40 \end{matrix}$

查看试题解析
7. 已知平行四边形ABCD，下列条件中，不能判定这个平行四边形为矩形的是（）

A、∠A=∠B B、∠A=∠C C、AC=BD D、AB⊥BC

查看试题解析
8. 随着“互联网＋”时代的到来，一种新型的打车方式受到大众欢迎．打车总费用y（单位：元）与行驶里程x（单位：千米）的函数关系如图所示．如果小明某次打车行驶里程为22千米，则他的打车费用为（）

A、33元 B、36元 C、40元 D、42元

查看试题解析
9. 如图，在正方形ABCD中，M、N是对角线AC上的两个动点，P是正方形四边上的任意一点，且AB=4，MN=2，设AM=x，在下列关于△PMN是等腰三角形和对应P点个数的说法中，
①当x=0（即M、A两点重合）时，P点有6个；

②当P点有8个时，x=2 $\sqrt{2}$ ﹣2；

③当△PMN是等边三角形时，P点有4个；

④当0＜x＜4 $\sqrt{2}$ ﹣2时，P点最多有9个．

其中结论正确是（　　）

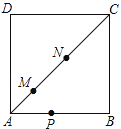A、①② B、①③ C、②③ D、③④

查看试题解析

二、填空题

10. $\sqrt{16}$ 等于（　　）

A、﹣4 B、4 C、±4 D、256

查看试题解析
11. 不等式 $3 x - 1 > 0$ 的解集是．

查看试题解析
12. 方程 $\frac{1}{x + 1} = \frac{x^{2}}{x + 1}$ 的根是

查看试题解析
13. 如果一次函数 $y = k x - 2 (k$ 是常数， $k \neq 0)$ 的图象经过点 $(2, 0)$ ，那么y的值随x的增大而 $($ 填“减小”或“增大” $)$

查看试题解析
14. 在三角形ABC中， $∠ C = 90 °$ ， $A C = 8$ ， $B C = 6$ ，D，E，F分别是AB，BC，CA的中点，G是重心，则 $G D =$ ．

查看试题解析
15. 在 $△ A B C$ 中，AD是BC边上的高， $B C = 12$ ， $A D = 8.$ 正方形EFGH的顶点E、F分别在AB、AC上，H、G在BC上．那么正方形EFGH的边长是．

查看试题解析
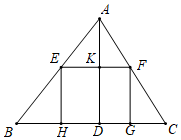16. 如图，定长弦CD在以AB为直径的⊙O上滑动（点C、D与点A、B不重合），M是CD的中点，过点C作CP⊥AB于点P，若CD=3，AB=8，PM=l，则l的最大值是

查看试题解析

三、解答题

17. 计算：

(1)、 ${(\frac{1}{2})}^{- 1} + {(π - 3.14)}^{0} + \sqrt[3]{- 8}$

(2)、 $\frac{{tan}^{2} 60 ° + 2 c o s 45 °}{2 s i n^{2} 60^{\circ} - c o s 60^{\circ}}$ ．

查看试题解析
18. 已知 ${\begin{array}{l} \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0) \dots \dots ① \\ x = m y + n (m \neq 0 ， n \neq 0) \dots \dots ② \end{array}$
求证： $(a^{2} + b^{2} m^{2}) y^{2} + 2 m n b^{2} y + (n^{2} - a^{2}) b^{2} = 0$ ．

查看试题解析
19. 如图，已知 $△ A B C$ 中， $A B = B C = 5$ ， $tan ∠ A B C = \frac{3}{4}$

(1)、利用直尺和圆规作线段BC的垂直平分线，交AB于点D，交BC于点 $E ($ 保留作图痕迹，不写作法 $)$

(2)、在（1）所作的图形中，求BD．

查看试题解析
20. 在平面直角坐标系xOy中，反比例函数 $y = \frac{k}{x} (k \neq 0)$ 的图象经过点 $A (- 5, \frac{8}{5})$ 与点 $B (- 2, m)$ ，抛物线 $y = a x^{2} + b x + c (a \neq 0)$ ，经过原点O，顶点是 $B (- 2, m)$ ，且与x轴交于另一点 $C (n, 0)$

(1)、求反比例函数的解析式与m的值；

(2)、求抛物线的解析式与n的值．

查看试题解析
21. 如图，圆O的半径为1，六边形ABCDEF是圆O的内接正六边形，从A，B，C，D，E，F六点中任意取两点，并连接成线段．

(1)、求线段长为2的概率；

(2)、求线段长为 $\sqrt{3}$ 的概率．

查看试题解析
22. 某商店订购了A，B两种商品，A商品28元 $/$ 千克，B商品24元 $/$ 千克，若B商品的数量比A商品的2倍少20千克，购进两种商品共用了2560元，求两种商品各多少千克？

查看试题解析
23. 如图，已知在⊙O中，AB是⊙O的直径，AC＝8，BC＝6．

(1)、求⊙O的面积；

(2)、若D为⊙O上一点，且△ABD为等腰三角形，求CD的长．

查看试题解析
24. 如图，四边形ABCD内接于 $⊙ O$ ，AD，BC的延长线交于点E，F是BD延长线上一点， $∠ C D E = \frac{1}{2} ∠ C D F = 60 °$ ．

(1)、求证： $△ A B C$ 是等边三角形；

(2)、判断DA，DC，DB之间的数量关系，并证明你的结论．

查看试题解析
25. 在平面直角坐标系xOy中，抛物线 $y = - x^{2} + b x + c$ 与x轴交于 $A (- 3 ， 0)$ ，点 $B (1 ， 0)$ 两点，与y轴交于点C

(1)、求抛物线的解析式：

(2)、若点P是抛物线上在第二象限内的一个动点，且点P的横坐标为t，连接PA、PC、AC．
$①$ 求 $△ A C P$ 的面积S关于t的函数关系式．

$②$ 求 $△ A C P$ 的面积的最大值，并求出此时点P的坐标．

查看试题解析