高中数学人教新课标A版必修四 第一章 三角函数 单元试卷
试卷更新日期:2020-03-25 类型:单元试卷
一、单选题
-
1. 函数的定义域是( )A、 B、 C、 D、2. 设 , , ,则( )A、 B、 C、 D、3. 若点 在第一象限,则在 内 的取值范围是( )
A、 B、 C、4. 已知函数f(x)=sin(ωx+ )(x∈R,ω>0)的最小正周期为π,将y=f(x)的图象向左平移|φ|个单位长度,所得函数y=f(x)为偶函数时,则φ的一个值是( )A、 B、 C、 D、5. 已知函数 的图像相邻的两个对称中心之间的距离为 ,若将函数 的图像向左平移 后得到偶函数 的图像,则函数 的一个单调递减区间为( )A、 B、 C、 D、6. 函数 的图像可能是( )A、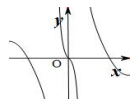 B、
B、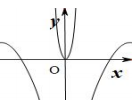 C、
C、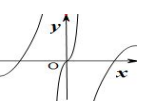 D、
D、 7. 如图,某地一天从 6 ~ 14 时的温度变化曲线近似满足函数: ,则中午 12 点时最接近的温度为( )
7. 如图,某地一天从 6 ~ 14 时的温度变化曲线近似满足函数: ,则中午 12 点时最接近的温度为( ) A、 B、 C、 D、8. 已知 满足 ,则g(x)=2cos(ωx+φ)在区间 [0,] 上的最大值为( )A、4 B、 C、1 D、﹣29. 已知 ,函数 在 上单调递减,则 的取值范围是( )A、 B、 C、 D、10. 函数 某相邻两支图象与坐标轴分别交于点 ,则方程 所有解的和为( )A、 B、 C、 D、11. 已知函数 的图象经过点 和 .若函数 在区间 上有唯一零点,则实数 的取值范围是( )A、 B、 C、 D、12. 已知函数 (其中 )的图象关于点 成中心对称,且与点 相邻的一个最低点为 ,则对于下列判断:①直线 是函数 图象的一条对称轴;②点 是函数 的一个对称中心;③函数 与 的图象的所有交点的横坐标之和为 .其中正确的判断是( )A、①② B、①③ C、②③ D、①②③
A、 B、 C、 D、8. 已知 满足 ,则g(x)=2cos(ωx+φ)在区间 [0,] 上的最大值为( )A、4 B、 C、1 D、﹣29. 已知 ,函数 在 上单调递减,则 的取值范围是( )A、 B、 C、 D、10. 函数 某相邻两支图象与坐标轴分别交于点 ,则方程 所有解的和为( )A、 B、 C、 D、11. 已知函数 的图象经过点 和 .若函数 在区间 上有唯一零点,则实数 的取值范围是( )A、 B、 C、 D、12. 已知函数 (其中 )的图象关于点 成中心对称,且与点 相邻的一个最低点为 ,则对于下列判断:①直线 是函数 图象的一条对称轴;②点 是函数 的一个对称中心;③函数 与 的图象的所有交点的横坐标之和为 .其中正确的判断是( )A、①② B、①③ C、②③ D、①②③二、填空题
-
13. 的值为 .14. 若 ,则 的值为.15. 将函数 的图象向右平移 个单位后,再向下平移1个单位得到函数 ,若 ,且 ,则 的最小值为 .16. 已知 , ,且 在区间 只有最小值,没有最大值,则 的值是 .
三、解答题
-
17. 某公司拟设计一个扇环形状的花坛(如图所示),该扇环是由以点O为圆心的两个同心圆弧和延长后通过点AD的两条线段围成.设圆弧 、 所在圆的半径分别为f(x)、R米,圆心角为θ(弧度).
 (1)、若θ= ,r1=3,r2=6,求花坛的面积;(2)、设计时需要考虑花坛边缘(实线部分)的装饰问题,已知直线部分的装饰费用为60元/米,弧线部分的装饰费用为90元/米,预算费用总计1200元,问线段AD的长度为多少时,花坛的面积最大?18. 化简计算:(1)、化简: .(2)、已知:sinαcosα= ,且 <α< ,求cosα﹣sinα的值.19. 已知角α的终边经过点 , 且 为第二象限角.(1)、求 、 、 的值;(2)、若 ,求 的值.20. 设函数 , 图像的一条对称轴是直线 .
(1)、若θ= ,r1=3,r2=6,求花坛的面积;(2)、设计时需要考虑花坛边缘(实线部分)的装饰问题,已知直线部分的装饰费用为60元/米,弧线部分的装饰费用为90元/米,预算费用总计1200元,问线段AD的长度为多少时,花坛的面积最大?18. 化简计算:(1)、化简: .(2)、已知:sinαcosα= ,且 <α< ,求cosα﹣sinα的值.19. 已知角α的终边经过点 , 且 为第二象限角.(1)、求 、 、 的值;(2)、若 ,求 的值.20. 设函数 , 图像的一条对称轴是直线 .(Ⅰ)求 的值并画出函数 在 上的图像;
(Ⅱ)若将 向左平移 个单位,得到 的图像,求使 成立的 的取值范围.
21. 已知点A(x1 , f(x1)),B(x2 , f(x2))是函数f(x)=2sin(ωx+φ)(ω>0,﹣ <φ<0)图象上的任意两点,且角φ的终边经过点P(1,﹣ ),若|f(x1)﹣f(x2)|=4时,|x1﹣x2|的最小值为(1)、求函数f(x)的解析式;(2)、若方程3[f(x)]2﹣f(x)+m=0在x∈( , )内有两个不同的解,求实数m的取值范围.22. 将函数y=sinx的图象上所有点的横坐标缩短到原来的 倍(纵坐标不变),再将所得的图象向左平移 个单位长度后得到函数f(x)的图象(1)、写出函数f(x)的解析式;(2)、若对任意的x∈[﹣ , ],f2(x)﹣mf(x)﹣1≤0恒成立,求实数m的取值范围;(3)、求实数a和正整数n,使得F(x)=f(x)﹣a在[0,nπ]上恰有2017个零点.