初中数学人教版七年级下学期 第五章 5.3.1 平行线的性质

试卷更新日期：2020-03-27 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 如图，一副直角三角板按如图所示的方式摆放，其中点 C 在 FD 的延长线上，且AB∥FC，则 ∠CBD 的度数为（    ）

    A、15° B、30° C、45° D、60°

    查看试题解析

  • 2. 如图，∠BCD＝95°，AB∥DE，则∠α与∠β满足（   ）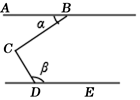

    A、∠α+∠β＝95° B、∠β﹣∠α＝95° C、∠α+∠β＝85° D、∠β﹣∠α＝85°

    查看试题解析

  • 3. 如图， ∠CED=60° ， DF⊥AB 于点F， DM//AC 交 AB 于点 M ， DE//AB 交 AC 于点 E ，则 ∠MDF 的度数是（   ）

    A、60° B、40° C、30° D、20°

    查看试题解析

  • 4. 如图，AB∥EF∥CD，∠ABC=46°，∠CEF=154°，则∠BCE 等于（    ）

    A、16° B、20° C、23° D、26°

    查看试题解析

二、填空题

  • 5. 如图：直线l1∥l2 ， 一块含30°角的直角三角板如图所示放置，∠1=25°，则∠2=.

    查看试题解析

  • 6. 如图，已知直线a∥b，∠1=40°，∠2=60°，则∠3=

    查看试题解析

  • 7. 如图，点 A 在直线DE上，若∠DAB=75°，∠ACF=141°，则当∠BAC=°时，DE∥BC．

    查看试题解析

三、解答题

  • 8. 如图所示，直线 a 、 b 被 c 、 d 所截，且  c⊥a，c⊥b，∠1=70°，求∠2的度数.


    查看试题解析

  • 9. 已知：如图，点E在直线DF上，点B在直线AC正，∠1=∠2， ∠3=∠4。

    求证：∠A=∠F


    查看试题解析

四、综合题

  • 10. 如图已知点E、F在直线AB上，点G在线段CD上，ED与FC交于点H，∠C=∠EFG，∠CED=∠GHD．


    (1)、求证：CE∥GF；
    (2)、试判断∠AED与∠D之间的数量关系，并说明理由；
    (3)、若∠EHF=100°，∠D=30°，求∠AEM的度数。

    查看试题解析