西藏自治区拉萨市2020年数学中考模拟试卷

试卷更新日期：2020-03-27 类型：中考模拟

进入出卷网下载

一、选择题（共12小题，满分36分，每小题3分）

1. 下列各数中，相反数是 $- \frac{1}{2}$ 的是（）

A、﹣ $\frac{1}{2}$ B、 $\frac{1}{2}$ C、﹣2 D、2

查看试题解析
2. 我国倡导的“一带一路”地区覆盖的总人口为4400000000人，这个数用科学记数法表示为（）

A、44×10⁸ B、4.4×10⁸ C、4.4×10⁹ D、44×10¹⁰

查看试题解析
3. 下列图案中是中心对称图形但不是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 下列各式中，计算正确的是（）

A、a³•a²＝a⁶ B、a³+a²＝a⁵ C、（a³）²＝a⁶ D、a⁶÷a³＝a²

查看试题解析
5. 如图，将一块含有30°角的直角三角板的两个顶点分别放在直尺的两条平行对边上，若∠α＝135°，则∠β等于（）

A、45° B、60° C、75° D、85°

查看试题解析
6. 如图，已知DE为△ABC的中位线，△ADE的面积为3，则四边形DECB的面积为（）

A、6 B、8 C、9 D、12

查看试题解析
7. 将抛物线y＝x²﹣2向左平移3个单位长度，再向上平移3个单位长度后，所得抛物线的解析式为（）

A、y＝（x+3）²+3 B、y＝（x﹣3）²+1 C、y＝（x+2）²+1 D、y＝（x+3）²+1

查看试题解析
8. 如图，在⊙ $O$ 中，半径 $O C$ 垂直弦 $A B$ 于 $D$ ，点 $E$ 在⊙ $O$ 上， $∠ E ＝ {22.5}^{°} ， A B ＝ 2$ ，则半径 $O B$ 等于（）

A、 $1$ B、 $\sqrt{2}$ C、 $2$ D、 $2 \sqrt{2}$

查看试题解析
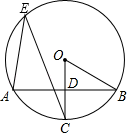9. 如图，正比例函数y＝kx与反比例函数y＝ $\frac{4}{x}$ 的图象相交于A、C两点，过点A作x轴的垂线交x轴于点B，连接BC，则△ABC的面积等于（）

A、8 B、6 C、4 D、2

查看试题解析
10. 如图，从一张腰长为60cm，顶角为120°的等腰三角形铁皮OAB中剪出一个最大扇形OCD，用剪下的扇形铁皮围成一个圆锥的侧面（不计损耗），则该圆锥的高为（）

A、10 cm B、15 cm C、10 $\sqrt{3}$ cm D、20 $\sqrt{2}$ cm

查看试题解析
11. 现有57本书，计划分给各学习小组，如每组6本则有剩余，每组7本却不够分，则学习小组共有（）

A、7个 B、8个 C、9个 D、10个

查看试题解析
12. 如图所示，在矩形ABCD中，AB＝4，AD＝3，矩形内部有一动点P满足S_△PAB＝ $\frac{1}{3}$ S_矩形ABCD ，则点P到A，B两点的距离之和PA+PB的最小值为（）

A、5 B、 $2 \sqrt{13}$ C、 $2 \sqrt{2}$ D、 $4 \sqrt{2}$

查看试题解析

二、填空题（共6小题，满分18分，每小题3分）

13. 因式分解：x²y﹣y³＝．

查看试题解析
14. 一元二次方程3x²＝4﹣2x的解是.

查看试题解析
15. 已知实数x，y满足|x﹣4|+ $\sqrt{y - 3}$ ＝0，则以x，y的值为两边长的直角三角形的周长是.

查看试题解析
16. 如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB于点D，AB＝25cm，BC＝15cm，则BD的长为cm.

查看试题解析
17. 如图，将宽为1cm的纸条沿BC折叠，使∠CAB＝45°，则折叠后重叠部分的面积为cm².

查看试题解析
18. 给定一列按规律排列的数： $- \frac{3}{2}$ ，1， $- \frac{7}{10}$ ， $\frac{9}{17}$ ，…，根据前4个数的规律，第2020个数是.

查看试题解析

三、解答题（共7小题，满分46分）

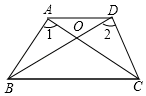
19. 计算：（﹣2）^﹣2+ $\frac{1}{2}$ cos60°﹣（ $\sqrt{3}$ ﹣2）⁰；

查看试题解析
20. 如图，在四边形ABCD中，AC、BD相交于点O，AB＝DC，∠1＝∠2.求证：AC＝BD.

查看试题解析
21. 某校研究学生的课余爱好情况，采取抽样调查的方法，从阅读、运动、娱乐、上网等四个方面调查了若干名学生的兴趣爱好，并将调査结果绘制成下面两幅不完整的统计图，请你根据图中提供的信息解答下列问题：

(1)、在这次调查中，求一共调查了多少名学生；

(2)、通过计算，补全条形统计图；

(3)、若该校爱好运动的学生共有600名，求该校共有学生大约有多少人？

(4)、在全校同学中随机选取一名学生参加演讲比赛，用频率估计概率，求选出的恰好是爱好阅读的学生的概率是多少？

查看试题解析
22. 列方程解应用题：
现有甲、乙两种机器加工零件，甲种机器比乙种机器每小时多加工30个，甲种机器加工900个零件所用时间与乙种机器加工600个零件所用时间相等，求两种机器每小时各加工多少个零件？

查看试题解析
23. 一艘航母在海上由西向东航行，到达A处时，测得小岛C位于它的北偏东70°方向，且与航母相距80海里，再航行一段时间后达到B处，测得小岛C位于它的北偏东37°方向，如果航母继续航行至小岛C的正南方向的D处，求还需航行的距离BD的长.
（参考数据：sin70°≈0.94；cos70°≈0.34；tan70°≈2.75；sin37°≈0.6；cos37°≈0.80；tan37°≈0.75）

查看试题解析
24. 如图，AB是⊙O的直径，点C是圆上一点，点D是半圆的中点，连接CD交OB于点E，点F是AB延长线上一点，CF＝EF.

(1)、求证：FC是⊙O的切线；

(2)、若CF＝5，tanA＝ $\frac{1}{2}$ ，求⊙O半径的长.

查看试题解析
25. 如图1，在平面直角坐标系中，点O为坐标原点，抛物线y＝ax²+bx+c与y轴交于点A（0，6），与x轴交于点B（﹣2，0），C（6，0）.

(1)、直接写出抛物线的解析式及其对称轴；

(2)、如图2，连接AB，AC，设点P（m，n）是抛物线上位于第一象限内的一动点，且在对称轴右侧，过点P作PD⊥AC于点E，交x轴于点D，过点P作PG∥AB交AC于点F，交x轴于点G.设线段DG的长为d，求d与m的函数关系式，并注明m的取值范围；

(3)、在（2）的条件下，若△PDG的面积为 $\frac{49}{12}$ ，
①求点P的坐标；

②设M为直线AP上一动点，连接OM交直线AC于点S，则点M在运动过程中，在抛物线上是否存在点R，使得△ARS为等腰直角三角形？若存在，请直接写出点M及其对应的点R的坐标；若不存在，请说明理由.

查看试题解析