湖北省武汉市蔡甸区求新联盟2020年九年级数学中考模拟试卷(3月)
试卷更新日期:2020-03-27 类型:中考模拟
一、选择题(每小题3分,共30分)
-
1. 介于下列哪两个整数之间( )A、0与1 B、1与2 C、2与3 D、3与42. 一元二次方程x2+2x=0的根是( )A、2 B、0 C、0或2 D、0或﹣23. 若△ABC∽△DEF, =2,△ABC面积为8,则△DEF的面积为( )A、1 B、2 C、4 D、84. 下列事件不是随机事件的是( )A、投两枚骰子,面朝上的点数之积为7 B、连续摸了两次彩票,均中大奖 C、投两枚硬币,朝上的面均为正面 D、NBA运动员连续投篮两次均未进5. 平面直角坐标系内一点P(﹣2,3)关于原点对称的点的坐标是( )A、(3,﹣2) B、(2,3) C、(﹣2,﹣3) D、(2,﹣3)6. 如图,AB是⊙O的直径,弦CD⊥AB,垂足为E,如果AB=20,CD=16,那么线段OE的长为( )
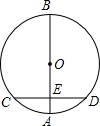 A、10 B、8 C、6 D、47. 将抛物线y=﹣2(x+1)2﹣2向左平移2个单位,向下平移3个单位后的新抛物线解析式为( )A、y=﹣2(x﹣1)2+1 B、y=﹣2(x+3)2﹣5 C、y=﹣2(x﹣1)2﹣5 D、y=﹣2(x+3)2+18. 如图,已知AB∥CD∥EF,那么下列结论正确的是( )
A、10 B、8 C、6 D、47. 将抛物线y=﹣2(x+1)2﹣2向左平移2个单位,向下平移3个单位后的新抛物线解析式为( )A、y=﹣2(x﹣1)2+1 B、y=﹣2(x+3)2﹣5 C、y=﹣2(x﹣1)2﹣5 D、y=﹣2(x+3)2+18. 如图,已知AB∥CD∥EF,那么下列结论正确的是( )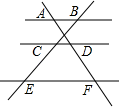 A、 = B、 = C、 = D、 =9. 下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )
A、 = B、 = C、 = D、 =9. 下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是( )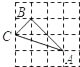 A、
A、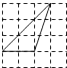 B、
B、 C、
C、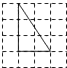 D、
D、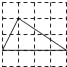 10. 已知⊙O,AB是直径,AB=4,弦CD⊥AB且过OB的中点,P是劣弧BC上一动点,DF垂直AP于F,则P从C运动到B的过程中,F运动的路径长度( )
10. 已知⊙O,AB是直径,AB=4,弦CD⊥AB且过OB的中点,P是劣弧BC上一动点,DF垂直AP于F,则P从C运动到B的过程中,F运动的路径长度( )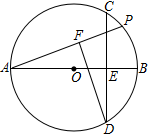 A、 π B、 C、 π D、2
A、 π B、 C、 π D、2二、填空题(每小题3分,共18分)
-
11. 计算:9+(﹣6)的结果为.12. 计算: ﹣ =.13. 经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转.如果这三种可能性大小相同,现有两辆汽车先后经过这个十字路口,则至少有一辆汽车向左转的概率是.14. 如图,矩形ABCD中,E为BC的中点,将△ABE沿直线AE折叠,使点B落在点F处,连接FC,若∠DAF=18°,则∠DCF=度.
 15. 已知Rt△ABC中,AC=3,BC=4,以C为圆心,以r为半径作圆.若此圆与线段AB只有一个交点,则r的取值范围为.
15. 已知Rt△ABC中,AC=3,BC=4,以C为圆心,以r为半径作圆.若此圆与线段AB只有一个交点,则r的取值范围为.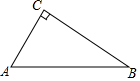 16. 已知△ABC中,∠ABC=45°,AB=7 ,BC=17,以AC为斜边在△ABC外作等腰Rt△ACD,连接BD,则BD的长为 .
16. 已知△ABC中,∠ABC=45°,AB=7 ,BC=17,以AC为斜边在△ABC外作等腰Rt△ACD,连接BD,则BD的长为 .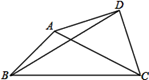
三、解答题(共8小题,共72分)
-
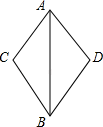
17. 解方程组: .18. 已知:如图,AC=AD,AB是∠CAD的角平分线.求证:BC=BD.
 19. 小明做游戏:游戏者分别转动如图的两个可以自由转动的转盘各一次,当两个转盘的指针所指数字都为x2﹣4x+3=0的根时,他就可以获得一次为大家表演节目的机会.
19. 小明做游戏:游戏者分别转动如图的两个可以自由转动的转盘各一次,当两个转盘的指针所指数字都为x2﹣4x+3=0的根时,他就可以获得一次为大家表演节目的机会. (1)、利用树状图或列表的方法(只选一种)表示出游戏可能出现的所有结果;(2)、求小明参加一次游戏就为大家表演节目的机会的概率是多少.20. 如图,在平面直角坐标系中,点A(0,4)、B(﹣3,0),将线段AB沿x轴正方向平移n个单位得到菱形ABCD.
(1)、利用树状图或列表的方法(只选一种)表示出游戏可能出现的所有结果;(2)、求小明参加一次游戏就为大家表演节目的机会的概率是多少.20. 如图,在平面直角坐标系中,点A(0,4)、B(﹣3,0),将线段AB沿x轴正方向平移n个单位得到菱形ABCD.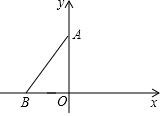 (1)、画出菱形ABCD,并直接写出n的值及点D的坐标;(2)、已知反比例函数y= 的图象经过点D,▱ABMN的顶点M在y轴上,N在y= 的图象上,求点M的坐标;(3)、若点A、C、D到某直线l的距离都相等,直接写出满足条件的直线解析式.21. 如图,AB为⊙O的直径,弦CD⊥AB于H,E为AB延长线上一点,CE交⊙O于点F
(1)、画出菱形ABCD,并直接写出n的值及点D的坐标;(2)、已知反比例函数y= 的图象经过点D,▱ABMN的顶点M在y轴上,N在y= 的图象上,求点M的坐标;(3)、若点A、C、D到某直线l的距离都相等,直接写出满足条件的直线解析式.21. 如图,AB为⊙O的直径,弦CD⊥AB于H,E为AB延长线上一点,CE交⊙O于点F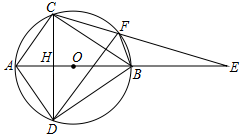 (1)、求证:BF平分∠DFE;(2)、若EF=DF,BE=5,AH= ,求⊙O的半径.22. 在锐角△ABC中,边BC长为18,高AD长为12
(1)、求证:BF平分∠DFE;(2)、若EF=DF,BE=5,AH= ,求⊙O的半径.22. 在锐角△ABC中,边BC长为18,高AD长为12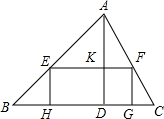 (1)、如图,矩形EFCH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K,求 的值;(2)、设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值.23. 如图,△ABC中,D是边BC的中点,E是AB边上一点,且AD⊥CE于O,AD=AC=CE.
(1)、如图,矩形EFCH的边GH在BC边上,其余两个顶点E、F分别在AB、AC边上,EF交AD于点K,求 的值;(2)、设EH=x,矩形EFGH的面积为S,求S与x的函数关系式,并求S的最大值.23. 如图,△ABC中,D是边BC的中点,E是AB边上一点,且AD⊥CE于O,AD=AC=CE.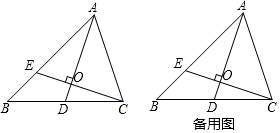 (1)、求证:∠B=45°;(2)、求 的值;(3)、直接写出 的值.24. 在平面直角坐标系中,抛物线y=﹣ x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点M为顶点,连接OM,若y与x的部分对应值如表所示:
(1)、求证:∠B=45°;(2)、求 的值;(3)、直接写出 的值.24. 在平面直角坐标系中,抛物线y=﹣ x2+bx+c与x轴交于A、B两点(点A在点B的左侧),点M为顶点,连接OM,若y与x的部分对应值如表所示:x
…
﹣1
0
3
…
y
…
0
0
…
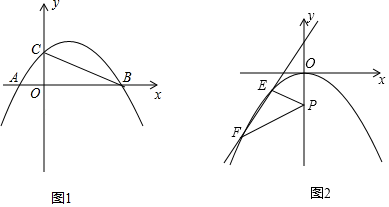 (1)、求抛物线的解析式;(2)、抛物线与y轴交于点C,点Q是直线BC下方抛物线上一点,点Q的横坐标为xQ.若S△BCQ≥ S△BOC , 求xQ的取值范围;(3)、如图2,平移此抛物线使其顶点为坐标原点,P(0,﹣1)为y轴上一点,E为抛物线上y轴左侧的一个动点,从E点发出的光线沿EP方向经过y轴上反射后与此抛物线交于另一点F.则当E点位置变化时,直线EF是否经过某个定点?如果是,请求出此定点的坐标;若不是,请说明理由.
(1)、求抛物线的解析式;(2)、抛物线与y轴交于点C,点Q是直线BC下方抛物线上一点,点Q的横坐标为xQ.若S△BCQ≥ S△BOC , 求xQ的取值范围;(3)、如图2,平移此抛物线使其顶点为坐标原点,P(0,﹣1)为y轴上一点,E为抛物线上y轴左侧的一个动点,从E点发出的光线沿EP方向经过y轴上反射后与此抛物线交于另一点F.则当E点位置变化时,直线EF是否经过某个定点?如果是,请求出此定点的坐标;若不是,请说明理由.