广西百色市2020年数学中考模拟试卷(一)
试卷更新日期:2020-03-27 类型:中考模拟
一、选择题(本大题共12小题,每小题3分,共36分.)
-
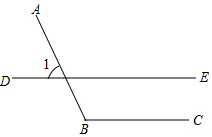
1. 三角形的外角和等于( )A、90° B、180° C、360° D、540°2. 如图,已知DE∥BC,若∠1=65°,则∠B的度数为( )
 A、135° B、115° C、105° D、65°3. 某班全体同学“运动与健康”评价等级的扇形统计图如图所示,则A等级所在扇形的圆心角度数为( )
A、135° B、115° C、105° D、65°3. 某班全体同学“运动与健康”评价等级的扇形统计图如图所示,则A等级所在扇形的圆心角度数为( )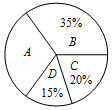 A、72° B、105° C、108° D、126°4. 方程组 的解是( )A、 B、 C、 D、5.
A、72° B、105° C、108° D、126°4. 方程组 的解是( )A、 B、 C、 D、5.如图,下列选项中不是正六棱柱三视图的是( )
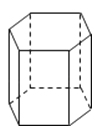 A、
A、 B、
B、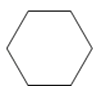 C、
C、 D、
D、 6. 地球上陆地的面积约为150 000 000 km2 , 把“150 000 000”用科学记数法表示为( )A、1.5×108 B、1.5×107 C、1.5×109 D、1.5×1067. 为丰富国民精神文化生活,提升文化素养,全国各地陆续开展全民阅读活动. 现在的图书馆不单是人们学习知识的地方,更是成为人们休闲的好去处. 下列图书馆标志的图形中不是轴对称图形的是( )A、
6. 地球上陆地的面积约为150 000 000 km2 , 把“150 000 000”用科学记数法表示为( )A、1.5×108 B、1.5×107 C、1.5×109 D、1.5×1067. 为丰富国民精神文化生活,提升文化素养,全国各地陆续开展全民阅读活动. 现在的图书馆不单是人们学习知识的地方,更是成为人们休闲的好去处. 下列图书馆标志的图形中不是轴对称图形的是( )A、 B、
B、 C、
C、 D、
D、 8. 已知a<b,下列不等式中,变形正确的是( )A、a﹣3>b﹣3 B、3a﹣1>3b﹣1 C、﹣3a>﹣3b D、 >9. 二次函数y=3(x﹣2)2﹣5与y轴交点坐标为( )A、(0,2) B、(0,﹣5) C、(0,7) D、(0,3)10. 某射击俱乐部将11名成员在某次射击训练中取得的成绩制成如图所示的条形统计图,由图可知,11名成员射击成绩的众数和中位数分别是( )
8. 已知a<b,下列不等式中,变形正确的是( )A、a﹣3>b﹣3 B、3a﹣1>3b﹣1 C、﹣3a>﹣3b D、 >9. 二次函数y=3(x﹣2)2﹣5与y轴交点坐标为( )A、(0,2) B、(0,﹣5) C、(0,7) D、(0,3)10. 某射击俱乐部将11名成员在某次射击训练中取得的成绩制成如图所示的条形统计图,由图可知,11名成员射击成绩的众数和中位数分别是( ) A、8,9 B、8,8 C、8,10 D、9,811. 下列命题的逆命题是真命题的是( )A、两直线平行,同位角相等 B、等边三角形是锐角三角形 C、如果两个实数是正数,那么它们的积是正数 D、全等三角形的对应角相等12. 在平面直角坐标系xOy中,点P(x0 , y0)到直线Ax+By+C=0的距离公式为d= ,例如:点P0(0,0)到直线4x+3y﹣3=0的距离为d= = ,根据以上材料,求点P1(3,4)到直线y=﹣ x+ 的距离为( )A、3 B、4 C、5 D、6
A、8,9 B、8,8 C、8,10 D、9,811. 下列命题的逆命题是真命题的是( )A、两直线平行,同位角相等 B、等边三角形是锐角三角形 C、如果两个实数是正数,那么它们的积是正数 D、全等三角形的对应角相等12. 在平面直角坐标系xOy中,点P(x0 , y0)到直线Ax+By+C=0的距离公式为d= ,例如:点P0(0,0)到直线4x+3y﹣3=0的距离为d= = ,根据以上材料,求点P1(3,4)到直线y=﹣ x+ 的距离为( )A、3 B、4 C、5 D、6二、填空题(本大题共6小题,每小题3分,共18分)
-
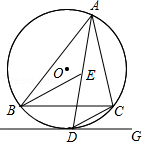
13. 化简:|﹣20|=.14. 在函数y= 中,自变量x的取值范围是 .15. “石头、剪刀、布”是民间广为流传的一种游戏,游戏时甲乙双方每次做“石头”“剪刀”“布”三种手势中的一种,并约定“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,同种手势不分胜负须继续比赛.假定甲、乙两人每次都是等可能地做这三种手势,那么一次游戏中乙获胜的概率是.16. 观察下列等式:1﹣ = ,2﹣ = ,3﹣ = ,4﹣ = ,…,根据你发现的规律,则第20个等式为.17. 如图,在平面直角坐标系中,已知△ABC与△DEF位似,原点O是位似中心, = ,若AB=1.5,则DE=.
 18. 如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于 BF的相同长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为16,∠C=60°,则四边形ABEF的面积是.
18. 如图,在平行四边形ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,大于 BF的相同长度为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF.若四边形ABEF的周长为16,∠C=60°,则四边形ABEF的面积是.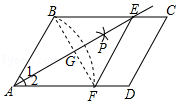
三、解答题(本大题共8小题,共66分.)
-
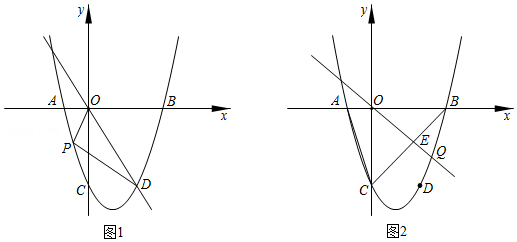
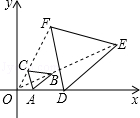
19. 计算:(﹣1)2020+(π﹣ )0﹣ tan30°+( )﹣1.20. 已知x是方程x2+3x=0的根,求代数式( +1)÷ 的值.21. 如图,一次函数y=﹣x+3的图象与反比例函数y= (k≠0)在第一象限的图象交于A(1,a)和B两点,与x轴交于点C.
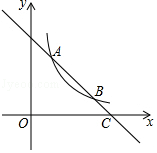 (1)、求反比例函数的解析式;(2)、若点P在x轴上,且△APC的面积为5,求点P的坐标.22. 如图,在▱ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE,EF与CD交于点G.
(1)、求反比例函数的解析式;(2)、若点P在x轴上,且△APC的面积为5,求点P的坐标.22. 如图,在▱ABCD中,点E在边BC上,点F在边AD的延长线上,且DF=BE,EF与CD交于点G.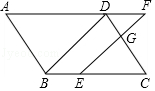 (1)、求证:BD∥EF.(2)、若BE=4,EC=6,△DGF的面积为8,求▱ABCD的面积.23. 为了庆祝中华人民共和国成立70周年,某市决定开展“我和祖国共成长”主题演讲比赛,某中学将参加本校选拔赛的40名选手的成绩(满分为100分,得分为正整数且无满分,最低为75分)分成五组,并绘制了下列不完整的统计图表.
(1)、求证:BD∥EF.(2)、若BE=4,EC=6,△DGF的面积为8,求▱ABCD的面积.23. 为了庆祝中华人民共和国成立70周年,某市决定开展“我和祖国共成长”主题演讲比赛,某中学将参加本校选拔赛的40名选手的成绩(满分为100分,得分为正整数且无满分,最低为75分)分成五组,并绘制了下列不完整的统计图表.分数段
频数
频率
74.5~79.5
2
0.05
79.5~84.5
m
0.2
84.5~89.5
12
0.3
89.5~94.5
14
n
94.5~99.5
4
0.1
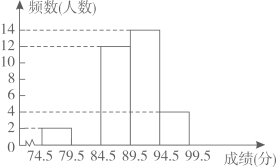 (1)、表中m= , n=;(2)、请在图中补全频数直方图;(3)、甲同学的比赛成绩是40位参赛选手成绩的中位数,据此推测他的成绩落在分数段内;(4)、选拔赛中,成绩在94.5分以上的选手,男生和女生各占一半,学校从中随机确定2名选手参加全市决赛,请用列举法或树状图法求恰好是一名男生和一名女生的概率.24. 某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为2400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30件,销售额增加840元.
(1)、表中m= , n=;(2)、请在图中补全频数直方图;(3)、甲同学的比赛成绩是40位参赛选手成绩的中位数,据此推测他的成绩落在分数段内;(4)、选拔赛中,成绩在94.5分以上的选手,男生和女生各占一半,学校从中随机确定2名选手参加全市决赛,请用列举法或树状图法求恰好是一名男生和一名女生的概率.24. 某商店以固定进价一次性购进一种商品,3月份按一定售价销售,销售额为2400元,为扩大销量,减少库存,4月份在3月份售价基础上打9折销售,结果销售量增加30件,销售额增加840元.
(1)、求该商店3月份这种商品的售价是多少元?(2)、如果该商店3月份销售这种商品的利润为900元,那么该商店4月份销售这种商品的利润是多少元?