广西百色市2020年数学中考模拟试卷(二)
试卷更新日期:2020-03-27 类型:中考模拟
一、选择题(本大题共12小题,每小题3分,共36分.)
-
1. ﹣ 的倒数是( )A、﹣2 B、 C、2 D、12. 如果一个多边形的内角和比外角和多180°,那么这个多边形是( )A、四边形 B、五边形 C、六边形 D、七边形3. 一组数据3、2、4、5、2,则这组数据的众数是( )A、2 B、3 C、3.2 D、44. 下列计算正确的是( )A、x3+x4=x7 B、(x+1)2=x2+1 C、(﹣a2b3)2=﹣a4b6 D、2a2•a﹣1=2a5. 若一个三角形的三边长分别为6、8、10,则这个三角形最长边上的中线长为( )A、3.6 B、4 C、4.8 D、56. 成人每天维生素D的摄入量约为0.0000046克.数据“0.0000046”用科学记数法表示为( )A、46×10﹣7 B、4.6×10﹣7 C、4.6×10﹣6 D、0.46×10﹣57. 如图是由4个完全一样的小正方体组成的几何体,这个几何体的主视图是( )
 A、
A、 B、
B、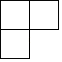 C、
C、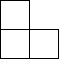 D、
D、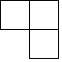 8. 按一定规律排列的一列数依次是 、1、 、 、 、 …按此规律,这列数中第100个数是( )A、 B、 C、 D、9. 甲、乙两名同学本学期五次引体向上的测试成绩(个数)成绩如图所示,下列判断正确的是( )
8. 按一定规律排列的一列数依次是 、1、 、 、 、 …按此规律,这列数中第100个数是( )A、 B、 C、 D、9. 甲、乙两名同学本学期五次引体向上的测试成绩(个数)成绩如图所示,下列判断正确的是( )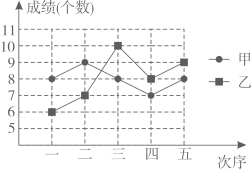 A、甲的成绩比乙稳定 B、甲的最好成绩比乙高 C、甲的成绩的平均数比乙大 D、甲的成绩的中位数比乙大10. 如图,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔60n mile的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处,这时,B处与灯塔P的距离为( )
A、甲的成绩比乙稳定 B、甲的最好成绩比乙高 C、甲的成绩的平均数比乙大 D、甲的成绩的中位数比乙大10. 如图,一艘海轮位于灯塔P的南偏东45°方向,距离灯塔60n mile的A处,它沿正北方向航行一段时间后,到达位于灯塔P的北偏东30°方向上的B处,这时,B处与灯塔P的距离为( )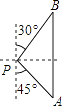 A、60 n mile B、60 n mile C、30 n mile D、30 n mile11. 在平面直角坐标系中,抛物线y=(x+5)(x﹣3)经变换后得到抛物线y=(x+3)(x﹣5),则这个变换可以是( )A、向左平移2个单位 B、向右平移2个单位 C、向左平移8个单位 D、向右平移8个单位12. 如图,在长方形纸片ABCD中,AB=4,AD=6.点E是AB的中点,点F是AD边上的一个动点.将△AEF沿EF所在直线翻折,得到△GEF.则GC长的最小值是( )
A、60 n mile B、60 n mile C、30 n mile D、30 n mile11. 在平面直角坐标系中,抛物线y=(x+5)(x﹣3)经变换后得到抛物线y=(x+3)(x﹣5),则这个变换可以是( )A、向左平移2个单位 B、向右平移2个单位 C、向左平移8个单位 D、向右平移8个单位12. 如图,在长方形纸片ABCD中,AB=4,AD=6.点E是AB的中点,点F是AD边上的一个动点.将△AEF沿EF所在直线翻折,得到△GEF.则GC长的最小值是( ) A、 B、 C、2 D、2
A、 B、 C、2 D、2二、填空题(本大题共6小题,每小题3分,共18分)
-
13. 因式分解:2ax2﹣4axy+2ay2=.14. 已知 ,则 =.15. 一个不透明的口袋中共有8个白球、5个黄球、5个绿球、2个红球,这些球除颜色外都相同。从口袋中随机摸出一个球,这个球是白球的概率是.16. 下列说法正确的是(填序号).
①在同一平面内,a,b,c为直线,若a⊥b,b⊥c,则a∥c;
②“若ac>bc,则a>b”的逆命题是真命题;
③若点M(a,2)与N(1,b)关于x轴对称,则a+b=﹣1;
④ 的整数部分是a,小数部分是b,则ab=3 ﹣3.
17. 三角形ABC中任意一点P(x0 , y0)经平移后対应点为P1(x0+5,y0+3),将三角形ABC作同样的平移得到三角形A1B1C1 , 若A(﹣2,3),则A1的坐标为.18. 某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:对于三个实数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{1,2,9}= =4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.
请结合上述材料,解决下列问题:
(1)、M{(﹣2)2 , 22 , ﹣22}=;(2)、若min{3﹣2x,1+3x,﹣5}=﹣5,则x的取值范围为.三、解答题(本大题共8小题,共66分,)
-
19. ( ﹣1)0+(﹣1)﹣2﹣4sin60°+ .20. 已知x,y满足方程组 ,求(x﹣y)2﹣(x+2y)(x﹣2y)的值.21. 如图,▱ABCD中,顶点A的坐标是(0,2),AD∥x轴,BC交y轴于点E,顶点C的纵坐标是﹣4,▱ABCD的面积是24.反比例函数y= 的图象经过点B和D,求:
 (1)、反比例函数的表达式;(2)、AB所在直线的函数表达式.22. 如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.
(1)、反比例函数的表达式;(2)、AB所在直线的函数表达式.22. 如图,矩形EFGH的顶点E,G分别在菱形ABCD的边AD,BC上,顶点F,H在菱形ABCD的对角线BD上.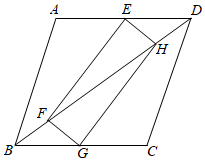 (1)、求证:BG=DE;(2)、若E为AD中点,FH=2,求菱形ABCD的周长.23. 某中学开设的体育选修课有篮球、足球、排球、羽毛球、乒乓球,学生可以根据自己的爱好选修其中1门.某班班主任对全班同学的选课情况进行了调查统计,制成了两幅不完整的统计图(图(1)和图(2)):
(1)、求证:BG=DE;(2)、若E为AD中点,FH=2,求菱形ABCD的周长.23. 某中学开设的体育选修课有篮球、足球、排球、羽毛球、乒乓球,学生可以根据自己的爱好选修其中1门.某班班主任对全班同学的选课情况进行了调查统计,制成了两幅不完整的统计图(图(1)和图(2)):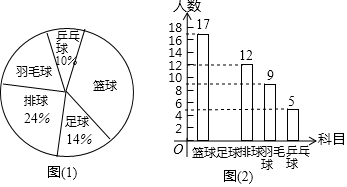 (1)、请你求出该班的总人数,并补全条形图(注:在所补小矩形上方标出人数);(2)、在该班团支部4人中,有1人选修排球,2人选修羽毛球,1人选修乒乓球.如果该班班主任要从他们4人中任选2人作为学生会候选人,那么选出的两人中恰好有1人选修排球、1人选修羽毛球的概率是多少?24. 随着城际铁路的开通,从甲市到乙市的高铁里程比快车里程缩短了90千米,运行时间减少了8小时,已知甲市到乙市的普快列车里程为1220千米,高铁平均时速是普快平均时速的2.5倍.(1)、求高铁列车的平均时速;(2)、若从甲市到乙市途经丙市,且从甲市到丙市的高铁里程为780千米.某日王老师要从甲市去丙市参加14:00召开的会议,如果他买了当日10:00从甲市到丙市的高铁票,而且从丙市高铁站到会议地点最多需要0.5小时.试问在高铁列车准点到达的情况下,王老师能否在开会之前赶到会议地点?25. 如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.
(1)、请你求出该班的总人数,并补全条形图(注:在所补小矩形上方标出人数);(2)、在该班团支部4人中,有1人选修排球,2人选修羽毛球,1人选修乒乓球.如果该班班主任要从他们4人中任选2人作为学生会候选人,那么选出的两人中恰好有1人选修排球、1人选修羽毛球的概率是多少?24. 随着城际铁路的开通,从甲市到乙市的高铁里程比快车里程缩短了90千米,运行时间减少了8小时,已知甲市到乙市的普快列车里程为1220千米,高铁平均时速是普快平均时速的2.5倍.(1)、求高铁列车的平均时速;(2)、若从甲市到乙市途经丙市,且从甲市到丙市的高铁里程为780千米.某日王老师要从甲市去丙市参加14:00召开的会议,如果他买了当日10:00从甲市到丙市的高铁票,而且从丙市高铁站到会议地点最多需要0.5小时.试问在高铁列车准点到达的情况下,王老师能否在开会之前赶到会议地点?25. 如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.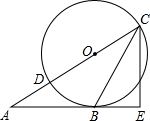 (1)、求证:CB平分∠ACE;(2)、若BE=3,CE=4,求⊙O的半径.26. 如图,在平面直角坐标系中,二次函数y=﹣x2+bx+c的图象与x轴交于A、B两点,A点的坐标为(﹣3,0),B点在原点的左侧,与y轴交于点C(0,3),点P是直线BC上方的抛物线上一动点
(1)、求证:CB平分∠ACE;(2)、若BE=3,CE=4,求⊙O的半径.26. 如图,在平面直角坐标系中,二次函数y=﹣x2+bx+c的图象与x轴交于A、B两点,A点的坐标为(﹣3,0),B点在原点的左侧,与y轴交于点C(0,3),点P是直线BC上方的抛物线上一动点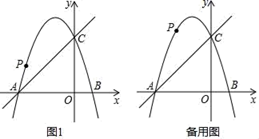 (1)、求这个二次函数的表达式;(2)、连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C(如图1所示),那么是否存在点P,使四边形POP′C为菱形?若存在,请此时点P的坐标:若不存在,请说明理由;(3)、当点P运动到什么位置时,四边形ABCP的面积最大,并求出其最大值.
(1)、求这个二次函数的表达式;(2)、连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C(如图1所示),那么是否存在点P,使四边形POP′C为菱形?若存在,请此时点P的坐标:若不存在,请说明理由;(3)、当点P运动到什么位置时,四边形ABCP的面积最大,并求出其最大值.