浙江省台州市椒江区2019-2020学年八年级上学期数学期末考试试卷
试卷更新日期：2020-03-27 类型：期末考试
一、选择题（每小题3分，共30分）
-
1. 下列图形中，不是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列代数运算正确的是（ ）A、(x3)2=x5 B、(2x)2=2x2 C、x3·x2=x5 D、x8÷x4=x23. 长度分别为a，2，4的三条线段能组成一个三角形，则a的值可能是（ ）.
A、1 B、2 C、3 D、64. 某种秋冬流感病毒的直径约为0.000000203米，该直径用科学记数法表示为（ ）米。A、 B、 C、 D、5. 如图，小峰从点O出发，前进5m后向右转45 ，再前进5m后又向右转45 ， …，这样一直走下去，他第一次回到出发点O时，一共走的路程是（ ）.
A、10米 B、20 米 C、40米 D、80米6. 如图，在△ABC中，AD为BC边上的中线，DE为△ABD中AB边上的中线，△ABC的面积为6，则△ADE的面积是（ ）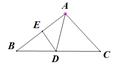
A、1 B、 C、2 D、7. 已知4y2+my+9是完全平方式，则m的值为（ ）A、6 B、12 C、±6 D、±128. 如图，已知△ABC，AB=5，∠ABC=60°，D为BC边上的点，AD=AC，BD=2，则DC=（ ）
A、0.5 B、1 C、1.5 D、29. 已知a-b=2，则a2−b2-4b的值为（ ）.A、2 B、4 C、6 D、810. 如图，在Rt△ABC中，∠C=90∘，∠B=30°，BC=7，点E在边BC上，并且CE=2，点F为边AC上的动点，将△CEF沿直线EF翻折，点C落在点P处，则点P到边AB距离的最小值是（ ）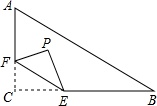
A、0.5 B、1 C、2 D、2.5二、填空题（每小题3分，共18分）
-
11. 若分式 有意义，则x的取值范围是.12. 已知点M(a，1)与点N(−2，b)关于y轴对称，则a-b=.13. 如图，将一副直角三角板，按如图所示叠放在一起，则图中∠COB=.
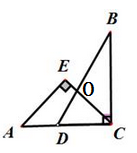14. 对于两个非零代数式，定义一种新的运算： .若 ，则x=.15. 若关于x的分式方程 的解为正数，则满足条件的非负整数K的值为.
16. 如图，在△ABC中，∠C=2∠A，过点C的直线能将△ABC分成两个等腰三角形，则∠A的度数为
三、解答题（共8小题，共52分）
-
17. 计算：(1)、(2)、18. 先化简，再求值： ，其中a=2.
19. 如图，已知AB∥CD，AC平分∠DAB.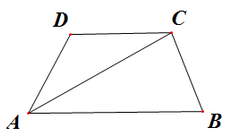
求证：△ADC是等腰三角形.
20. △ABC在平面直角坐标系中的位置如图所示.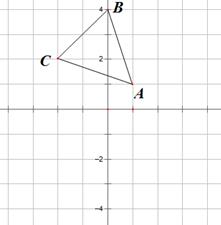
(1)、作出△ABC关于y轴对称的△A1B1C1；(2)、点P在x轴上，且点P到点A与点C的距离之和最小，直接写出点P的坐标为.21. 某校庆为祝建国70周年举行“爱国读书日”活动，计划用500元购买某种爱国主义读书，现书店打八折，用500元购买的爱国主义读本比原计划多了5本，求该爱国主义读本原件多少元？22. 如图，已知△ABC，
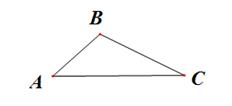(1)、求作点P，使点P到B、C两点的距离相等，且点P到∠BAC两边的距离也相等（尺规作图，保留作图痕迹，不写作法）.(2)、在（1）中，连接PB、PC，若∠BAC=40°，求∠BPC的度数.23. 【阅读材科】小明同学发现这样一个规律：两个顶角相等的等腰三角形，如果具有公共的项角的顶点，并把它们的底角顶点连接起来则形成一组全等的三角形，小明把具有这个规律的图形称为“手拉手”图形.如图1，在“手拉手” 图形中，小明发现若∠BAC= ∠DAE， AB=AC， AD=AE，则△ABD≌△ACE.
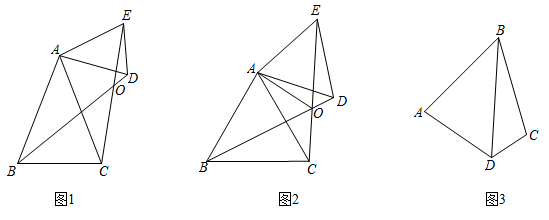(1)、【材料理解】在图1中证明小明的发现.
(2)、【深入探究】如图2，△ABC和△AED是等边三角形，连接BD， EC交于点O，连接AO，下列结论：①BD=EC；②∠BOC=60°；③∠AOE=60°；④EO=CO，其中正确的有 . (将所有正确的序号填在横线上).
(3)、【延伸应用】如图3， AB=BC，∠ABC=∠BDC= 60°，试探究∠A与∠C的数量关系。