浙江省衢州市2020年中考数学模拟试卷1
试卷更新日期:2020-03-27 类型:中考模拟
一、选择题(本大题共10小题,每小题3分,共30分。)
-
1. 如图,将一个圆柱体放置在长方体上,其中圆柱体的底面直径与长方体的宽相平,则该几何体的左视图是( )
 A、
A、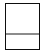 B、
B、 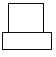 C、
C、 D、
D、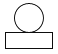 2. 北京国家体育场“鸟巢”建筑面积为258000m2 , 数字258000用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、x2•x3=x5 B、x6÷x2=x3 C、x3+x3=x6 D、2x﹣x=24. 在平直角坐标系中,已知点A(﹣4,0),B(2,0),若点C在一次函数y=﹣ x+2的图象,且△ABC为等腰三角形,则满足条件的点C有( )A、2个 B、3个 C、4个 D、5个5. 下列各数中,是负数的是( )A、﹣(﹣2) B、(﹣2)2 C、|﹣2| D、﹣226. 一个不透明的盒子中装有3个白球、9个红球,这些球除颜色外,没有任何其他区别,现从这个盒子中随机摸出一个球,摸到红球的可能性是( )A、 B、 C、 D、7. 等腰三角形的一个底角是 ,则它的顶角是( )A、 B、 C、 D、8. 正三角形的外接圆的半径和高的比为( )A、1:2 B、2:3 C、3:4 D、1:9. 关于二次函数 ,下列叙述正确的是( )A、顶点坐标为 B、当 时, 有最大值是2 C、对称轴为直线 D、当 时, 随 的增大而减小10. 如图,⊙O过点B、C,圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )
2. 北京国家体育场“鸟巢”建筑面积为258000m2 , 数字258000用科学记数法表示为( )A、 B、 C、 D、3. 下列计算正确的是( )A、x2•x3=x5 B、x6÷x2=x3 C、x3+x3=x6 D、2x﹣x=24. 在平直角坐标系中,已知点A(﹣4,0),B(2,0),若点C在一次函数y=﹣ x+2的图象,且△ABC为等腰三角形,则满足条件的点C有( )A、2个 B、3个 C、4个 D、5个5. 下列各数中,是负数的是( )A、﹣(﹣2) B、(﹣2)2 C、|﹣2| D、﹣226. 一个不透明的盒子中装有3个白球、9个红球,这些球除颜色外,没有任何其他区别,现从这个盒子中随机摸出一个球,摸到红球的可能性是( )A、 B、 C、 D、7. 等腰三角形的一个底角是 ,则它的顶角是( )A、 B、 C、 D、8. 正三角形的外接圆的半径和高的比为( )A、1:2 B、2:3 C、3:4 D、1:9. 关于二次函数 ,下列叙述正确的是( )A、顶点坐标为 B、当 时, 有最大值是2 C、对称轴为直线 D、当 时, 随 的增大而减小10. 如图,⊙O过点B、C,圆心O在等腰直角△ABC的内部,∠BAC=90°,OA=1,BC=6,则⊙O的半径为( )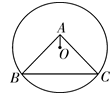 A、2 B、 C、4 D、3
A、2 B、 C、4 D、3二、填空题(本大题共6小题,每小题4分,共24分)
-
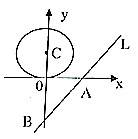
11. 。12. 计算: =.13. 已知一组数据6,6,5,x,1,请你给正整数x一个值 , 使这组数据的众数为6,中位数为5.14. 在△ABC中,已知AB=2,∠B=30°,AC= .则S△ABC=.15. 如图,若直线 与 轴、 轴分别交于点 、 ,并且 , ,一个半径为 的 ,圆心 从点 开始沿 轴向下运动,当 与直线 相切时, 运动的距离是 .
 16. 如图,点A(-2,0),B(0,1),以线段AB为边在第二象限作矩形ABCD,双曲线 (k<0)经过点D,连接BD,若四边形OADB的面积为6,则k的值是.
16. 如图,点A(-2,0),B(0,1),以线段AB为边在第二象限作矩形ABCD,双曲线 (k<0)经过点D,连接BD,若四边形OADB的面积为6,则k的值是.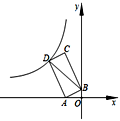
三、解答题(本大题共7小题,共66分)
-
17. 计算:
18. 如图所示, 点在 格中的格点上.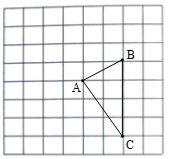
①画出 A逆时针旋转 的
②在图中确定格点D,并画出一个以A、B、C、D为顶点的四边形,使其为中心对称图形.
19. 如图,已知在△ABC中,BC边上的高AD与AC边上的高BE交于点F,且∠BAC=45°,BD=6,CD=4,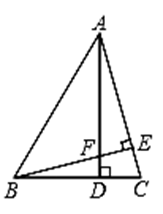 (1)、求证: △AEF ≌ △BEC
(1)、求证: △AEF ≌ △BEC
(2)、求△ABC的面积
20. 如图,直线y=kx+k交x轴,y轴分别于A,C,直线BC过点C交x轴于B,OC=3OA,∠CBA=45∘.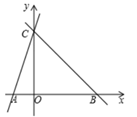 (1)、求直线BC的解析式;
(1)、求直线BC的解析式;
(2)、动点P从A出发沿射线AB匀速运动,速度为2个单位/秒,连接CP,设△PBC的面积为S,点P的运动时间为t秒,求S与t之间的函数关系式,直接写出t的取值范围;
21. “垃圾不落地,商南更美丽”。某中学为了了解七年级学生对这个一倡议的落实情况,学校安排政教处在七年级学生中随机抽取了部分学生,并针对学生“是否随手丢垃圾”这一情况进行了问卷调查,将这一情况分为: ——从不随手丢垃圾; ——偶尔随手丢垃圾; ——经常随手丢垃圾三项。要求每位被调查的学生必须从以上三项中选一项且只能选一项。现将调查结果绘制成以下两幅不完整的统计图。请你根据以上信息,解答下列问题: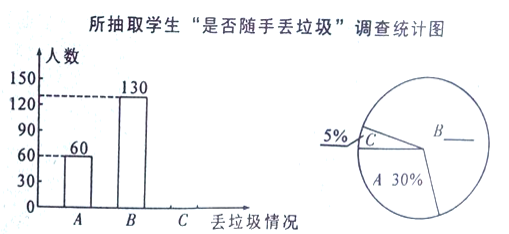 (1)、补全条形统计图和扇形统计图;
(1)、补全条形统计图和扇形统计图;
(2)、图中“偶尔随手丢垃圾”所在扇形的圆心角为;
(3)、若该校七年级共有1500名学生,请你估计该年级学生中“经常随手丢垃圾”的学生约有多少人?谈谈你的看法?
22. 某家电销售商场电冰箱的销售价为每台1600元,空调的销售价为每台1400元,每台电冰箱的进价比每台空调的进价多300元,商场用9000元购进电冰箱的数量与用7200元购进空调数量相等.(1)、求每台电冰箱与空调的进价分别是多少?
(2)、现在商场准备一次购进这两种家电共100台,设购进电冰箱x台,这100台家电的销售利润为Y元,要求购进空调数量不超过电冰箱数量的2倍,总利润不低于16200元,请分析合理的方案共有多少种?
(3)、实际进货时,厂家对电冰箱出厂价下调K(0<K<150)元,若商场保持这两种家电的售价不变,请你根据以上信息及(2)中条件,设计出使这100台家电销售总利润最大的进货方案.
23. 在矩形ABCD中,AB=8cm,BC=6cm,点P从点A出发,沿AB边向点B以每秒2cm的速度移动,同时点Q从点D出发沿DA边向点A以每秒1cm的速度移动,P、Q其中一点到达终点时,另一点随之停止运动.设运动时间为t秒.回答下列问题: (1)、如图①,几秒后△APQ的面积等于5cm2.
(1)、如图①,几秒后△APQ的面积等于5cm2.
(2)、如图②,若以点P为圆心,PQ为半径作⊙P.在运动过程中,是否存在t值,使得点C落在⊙P上?若存在,求出t的值;若不存在,请说明理由.
(3)、如图③,若以Q为圆心,DQ为半径作⊙Q,当⊙Q与AC相切时①求t的值.
②如图④,若点E是此时⊙Q上一动点,F是BE的中点,请直接写出CF的最小值.
24. 如图菱形ABCD中,∠ADC=60°,M、N分别为线段AB,BC上两点,且BM=CN,且AN,CM所在直线相交于E.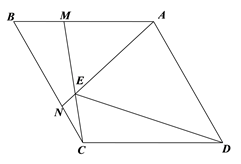 (1)、证明△BCM≌△CAN;
(1)、证明△BCM≌△CAN;
(2)、∠AEM=°;
(3)、求证DE平分∠AEC;
(4)、试猜想AE,CE,DE之间的数量关系并证明.