浙江省湖州市2020年中考数学模拟试卷1

试卷更新日期：2020-03-27 类型：中考模拟

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分。在每小题给出的四个选项中，只有一个选项是符合题目要求的）

1. 8的倒数是（）

A、 ﹣8 B、8 C、﹣ $\frac{1}{8}$ D、 $\frac{1}{8}$

查看试题解析
2. 在“流浪地球”的影片中地球要摆脱太阳引力，必须靠外力推动达到逃逸速度，已知地球绕太阳公转的速度约为110000km/h，这个数用科学记数法表示为（单位：km/h）（）

A、0.11×10⁴ B、0.11×10⁶ C、1.1×10⁵ D、1.1×10⁴

查看试题解析
3. 甲、乙两人赛跑，则开始起跑时都迈出左腿的概率是（）

A、1 B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{4}$

查看试题解析
4. 已知 $∠ 1 = 75 °$ ，则 $∠ 1$ 的余角是（）

A、 $15 °$ B、 $25 °$ C、 $75 °$ D、 $105 °$

查看试题解析
5. 圆锥的底面面积为 $16 π {cm}^{2}$ ，母线长为 $6 cm$ ，则这个圆锥的侧面积为（）

A、 $24 c m^{2}$ B、 $24 π c m^{2}$ C、 $48 c m^{2}$ D、 $48 π c m^{2}$

查看试题解析
6. 化简 $\frac{x^{2}}{y - x} - \frac{x y}{y - x}$ ＝（）

A、﹣x B、y﹣x C、x﹣y D、﹣x﹣y

查看试题解析
7. 如图，在 $Rt △ A B C$ 中，已知 $∠ C = 90^{\circ}$ ， $B D$ 平分 $∠ A B C$ ， $D E ⊥ A B$ 于点 $E$ ，则下列结论错误的是（）

A、 $D E = C D$ B、 $A C = D E + A D$ C、 $D E$ 平分 $∠ A D B$ D、 $∠ A B D = ∠ D B C$

查看试题解析
8. 如图，在△ABC中，点D，E分别在边AC，AB上，BD与CE交于点O，给出下列四个条件：①∠EBO=∠DCO；②BE=CD；③OB=OC；④OE=OD．从上述四个条件中，选取两个条件，不能判定△ABC是等腰三角形的是（　　）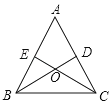

A、①② B、①③ C、③④ D、②③

查看试题解析
9. 如图所示，在四边形 $A B C D$ 中， $A D ⊥ A B$ ， $∠ C = 110^{°}$ ，它的一个外角 $∠ A D E = 60^{°}$ ，则 $∠ B$ 的大小是（）

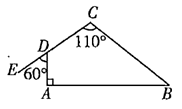A、70° B、60° C、40° D、30°

查看试题解析
10. 如图，抛物线y=ax²+bx+c（a≠0）与x轴交于（-1，0），（3，0）两点，则下列说法：①abc＜0；②a-b+c=0；③2a+b=0；④2a+c＞0；⑤若A（x₁ ， y₁），B（x₂ ， y₂），C（x₃ ， y₃）为抛物线上三点，且-1＜x₁＜x₂＜1，x₃＞3，则y₂＜y₁＜y₃ ，其中正确的结论是（）

A、 $① ⑤$ B、 $② ④$ C、 $② ③ ④$ D、 $② ③ ⑤$

查看试题解析

二、填空题（本大题共6小题，每小题4分，共24分）

11. 分解因式4x²－(y－2)²＝.

查看试题解析
12. 某公司欲招聘一名公关人员，对甲、乙两位候选人进行了面试和笔试，他们的成绩如表：

候选人

甲

乙

测试成绩(百分制)

面试

86

92

笔试

90

83

如果公司认为，作为公关人员面试的成绩应该比笔试的成绩更重要，并分别赋予它们6和4的权。根据两人的平均成绩，公司将录取.

查看试题解析
13. 如图，梯形ABCD内接于圆O，AB∥CD，AB为直径，DO平分∠ADC，则∠DAO的度数是.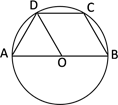

查看试题解析
14. 如图，正方形ABCD中，M、N分别为BC、CD的中点，连结AM、AC交BN与E、F，则EF：FN的值是.

查看试题解析
15. 设函数y=x+5与y= $\frac{3}{x}$ 的的两个交点的横坐标为a、b，则 $\frac{1}{a} + \frac{1}{b}$ 是.

查看试题解析
16. 在△ABC中，AC=6 $\sqrt{5}$ ，点D为直线AB上一点，且AB=3BD，直线CD与直线BC所夹锐角的正切值为 $\frac{1}{2}$ ，并且CD⊥AC，则BC的长为．

查看试题解析

三、解答题

17. 计算： $\sqrt[3]{- 8} - 3 \tan 30 ° + {(π - 3.14)}^{0} + {(\frac{1}{2})}^{- 1}$ .

查看试题解析
18.

(1)、已知 $| a | = 3$ ， $b^{2} = 25$ ，且 $a + b < 0$ ，求 $a - b$ 的值.

(2)、先化简，再求值： $3 x^{2} - [7 x - (4 x - 3) - 2 x^{2}]$ ，其中 $x = - \frac{1}{2}$ .

查看试题解析
19. 如图所示， $M$ 是 $△ A B C$ 的边 $B C$ 的中点， $A N$ 平分 $∠ B A C$ ， $B N ⊥ A N$ 于点 $N$ ，延长 $B N$ 交 $A C$ 于点 $D$ ，且 $A B = 10$ ， $B C = 15$ ， $M N = 3$ .

(1)、求证： $B N = D N$ .

(2)、求 $△ A B C$ 的周长.

查看试题解析
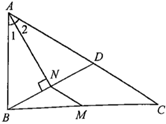20. 课题小组从某市20000名九年级男生中，随机抽取了1000名进行50米跑测试，并根据测试结果绘制了如下尚不完整的统计图表.

等级

人数/名

优秀

a

良好

b

及格

150

不及格

50

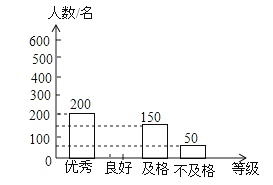
解答下列问题：

(1)、a等于多少？，b等于多少？

(2)、补全条形统计图；

(3)、试估计这20000名九年级男生中50米跑达到良好和优秀等级的总人数.

查看试题解析
21. 如图，直线y＝kx＋6与x轴，y轴分别相交于点A，B，O为坐标原点，点A的坐标为(－8，0).

(1)、求k的值；

(2)、若点P(x，y)是第二象限内直线上的一个动点，在点P的运动过程中，试写出△OPA的面积S与x之间的函数关系式，并写出自变量的取值范围；

(3)、若点P(0，m)为射线BO(B，O两点除外)上的一动点，过点P作PC⊥y轴交直线AB于C，连接PA.设△PAC的面积为S′，求S′与m的函数关系式，并写出自变量m的取值范围.

查看试题解析
22. 如图1，△ABC的边BC在直线l上，AC⊥BC，且AC=BC；△EFP的边FP也在直线l上，边EF与边AC重合，且EF=FP.

(1)、将△EFP沿直线l向左平移到图2的位置时，EP交AC于点Q，连接AP，BQ.猜想并写出BQ与AP所满足的数量关系，请证明你的猜想；

(2)、将△EFP沿直线l向左平移到图3的位置时，EP的延长线交AC的延长线于点Q，连接AP，BQ.你认为（1）中所猜想的BQ与AP的数量关系还成立吗？若成立，给出证明；若不成立，请说明理由；

(3)、若AC=BC=4，设△EFP平移的距离为x，当0≤x≤8时，△EFP与△ABC重叠部分的面积为S，请写出S与x之间的函数关系式，并求出最大值.

查看试题解析
23. 如图，在 $▱ A B C D$ 中， $A B ⊥ A C$ ，对角线 $A C$ 、 $B D$ 相交于点 $O$ ，将直线 $A C$ 绕点 $O$ 顺时针旋转一个角度 $α$ （ $0 ° < α ⩽ 90 °$ ），分别交线段 $B C$ 、 $A D$ 于点 $E$ 、 $F$ ，已知 $A B = 1$ ， $B C = \sqrt{5}$ ，连接 $B F$ .

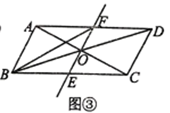(1)、如图①，在旋转的过程中，请写出线段 $A F$ 与 $E C$ 的数量关系，并证明；

(2)、如图②，当 $α = 45 °$ 时，请写出线段 $B F$ 与 $D F$ 的数量关系，并证明；

(3)、如图③，当 $α = 90 °$ 时，求 $△ B O F$ 的面积.

查看试题解析
24. 如图，已知抛物线 $y = a x^{2} + \frac{3}{2} x + 4$ 的对称轴是直线x=3，且与x轴相交于A，B两点（B点在A点右侧）与y轴交于C点．

(1)、求抛物线的解析式和A、B两点的坐标；

(2)、若点P是抛物线上B、C两点之间的一个动点（不与B、C重合），则是否存在一点P，使△PBC的面积最大．若存在，请求出△PBC的最大面积；若不存在，试说明理由；

(3)、若M是抛物线上任意一点，过点M作y轴的平行线，交直线BC于点N，当MN=3时，求M点的坐标．

查看试题解析

候选人		甲	乙
测试成绩(百分制)	面试	86	92
测试成绩(百分制)	笔试	90	83

等级	人数/名
优秀	a
良好	b
及格	150
不及格	50