浙江省台州市玉环市2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-03-27 类型:期末考试
一、单选题
-
1. 下列事件中,是必然事件的是( )A、购买一张彩票,中奖 B、射击运动员射击一次,命中靶心 C、任意画一个三角形,其内角和是180° D、经过有交通信号灯的路口,遇到红灯2. 中, ,若 , ,则 的长为( )A、 B、 C、 D、53. 若点 , , 都在反比例函数 的图象上,则 , , 的大小关系是( )A、 B、 C、 D、4. 如图,在 中, .以 为直径作半圆 ,交 于点 ,交 于点 ,若 ,则 的度数是( )
 A、 B、 C、 D、5. 在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”,“兵”所在位置的格点构成的三角形相似( )
A、 B、 C、 D、5. 在如图所示的象棋盘(各个小正方形的边长均相等)中,根据“马走日”的规则,“马”应落在下列哪个位置处,能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”,“兵”所在位置的格点构成的三角形相似( ) A、①处 B、②处 C、③处 D、④处6. 如图,二次函数 的图象经过点 , ,下列说法正确的是( )
A、①处 B、②处 C、③处 D、④处6. 如图,二次函数 的图象经过点 , ,下列说法正确的是( )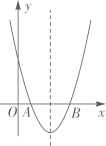 A、 B、 C、 D、图象的对称轴是直线7. 如图,某同学用圆规 画一个半径为 的圆,测得此时 ,为了画一个半径更大的同心圆,固定 端不动,将 端向左移至 处,此时测得 ,则 的长为( )
A、 B、 C、 D、图象的对称轴是直线7. 如图,某同学用圆规 画一个半径为 的圆,测得此时 ,为了画一个半径更大的同心圆,固定 端不动,将 端向左移至 处,此时测得 ,则 的长为( ) A、 B、 C、 D、8. 已知点 是一次函数 的图像和反比例函数 的图象的交点,当一次函数的值大于反比例函数的值时, 的取值范围是( )A、 或 B、 C、 或 D、9. 如图, 为线段 上一动点(点 不与点 、 重合),在线段 的同侧分别作等边 和等边 ,连结 、 ,交点为 .若 ,求动点 运动路径的长为( )
A、 B、 C、 D、8. 已知点 是一次函数 的图像和反比例函数 的图象的交点,当一次函数的值大于反比例函数的值时, 的取值范围是( )A、 或 B、 C、 或 D、9. 如图, 为线段 上一动点(点 不与点 、 重合),在线段 的同侧分别作等边 和等边 ,连结 、 ,交点为 .若 ,求动点 运动路径的长为( ) A、 B、 C、 D、10. 在平面直角坐标系xOy中,已知点M,N的坐标分别为(﹣1,2),(2,1),若抛物线y=ax2﹣x+2(a≠0)与线段MN有两个不同的交点,则a的取值范围是( )A、a≤﹣1或 ≤a< B、 ≤a< C、a≤ 或a> D、a≤﹣1或a≥
A、 B、 C、 D、10. 在平面直角坐标系xOy中,已知点M,N的坐标分别为(﹣1,2),(2,1),若抛物线y=ax2﹣x+2(a≠0)与线段MN有两个不同的交点,则a的取值范围是( )A、a≤﹣1或 ≤a< B、 ≤a< C、a≤ 或a> D、a≤﹣1或a≥二、填空题
-
11. 将抛物线 向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线解析式为.12. 某水果公司以2.2元/千克的成本价购进 苹果.公司想知道苹果的损坏率,从所有苹果中随机抽取若干进行统计,部分数据如下:
苹果损坏的频率
0.106
0.097
0.102
0.098
0.099
0.101
估计这批苹果损坏的概率为精确到0.1),据此,若公司希望这批苹果能获得利润23000元,则销售时(去掉损坏的苹果)售价应至少定为元/千克.
13. 如图,是某同学制作的一个圆锥形纸帽的示意图,则围成这个纸帽的纸的面积为. 14. 如图,在 中, 在 边上, , 是 的中点,连接 并延长交 于 ,则 .
14. 如图,在 中, 在 边上, , 是 的中点,连接 并延长交 于 ,则 . 15. 如图,过原点的直线与反比例函数 ( )的图象交于 , 两点,点 在第一象限.点 在 轴正半轴上,连结 交反比例函数图象于点 . 为 的平分线,过点 作 的垂线,垂足为 ,连结 .若 是线段 中点, 的面积为4,则 的值为.
15. 如图,过原点的直线与反比例函数 ( )的图象交于 , 两点,点 在第一象限.点 在 轴正半轴上,连结 交反比例函数图象于点 . 为 的平分线,过点 作 的垂线,垂足为 ,连结 .若 是线段 中点, 的面积为4,则 的值为.
三、解答题
-
16. 如图, 内接于半径为 的半 , 为直径,点 是弧 的中点,连结 交 于点 , 平分 交 于点 ,则 .若点 恰好为 的中点时, 的长为.
 17. 如图,在下列 (边长为1)的网格中,已知 的三个顶点 , , 在格点上,请分别按不同要求在网格中描出一个点,并写出点的坐标.
17. 如图,在下列 (边长为1)的网格中,已知 的三个顶点 , , 在格点上,请分别按不同要求在网格中描出一个点,并写出点的坐标. (1)、经过 , , 三点有一条抛物线,请在图1中描出点 ,使点 落在格点上,同时也落在这条抛物线上;则点 的坐标为;(2)、经过 , , 三点有一个圆,请用无刻度的直尺在图2中画出圆心 ;写出点 的坐标.18. 我市某校准备成立四个活动小组: .声乐, .体育, .舞蹈, .书画,为了解学生对四个活动小组的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中必须选择而且只能选择一个小组,根据调查结果绘制如下两幅不完整的统计图.
(1)、经过 , , 三点有一条抛物线,请在图1中描出点 ,使点 落在格点上,同时也落在这条抛物线上;则点 的坐标为;(2)、经过 , , 三点有一个圆,请用无刻度的直尺在图2中画出圆心 ;写出点 的坐标.18. 我市某校准备成立四个活动小组: .声乐, .体育, .舞蹈, .书画,为了解学生对四个活动小组的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中必须选择而且只能选择一个小组,根据调查结果绘制如下两幅不完整的统计图.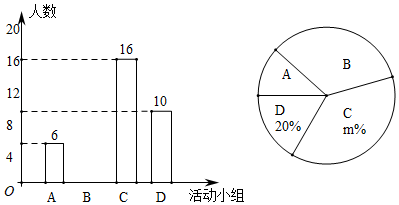
请结合图中所给信息,解答下列问题:
(1)、本次抽样调查共抽查了名学生,扇形统计图中的 值是;(2)、请补全条形统计图;(3)、喜爱“书画”的学生中有两名男生和两名女生表现特别优秀,现从这4人中随机选取两人参加比赛,请用列表或画树状图的方法求出所选的两人恰好是一名男生和一名女生的概率.19. 小李要外出参加“建国70周年”庆祝活动,需网购一个拉杆箱,图①,②分别是她上网时看到的某种型号拉杆箱的实物图与示意图,并获得了如下信息:滑杆 ,箱长 ,拉杆 的长度都相等, 在 上, 在 上,支杆 ,请根据以上信息,解决下列向题.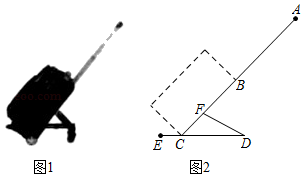 (1)、求 的长度(结果保留根号);(2)、求拉杆端点 到水平滑杆 的距离(结果保留根号).20. 如图, 中, , , 平分 ,交 轴于点 ,点 是 轴上一点, 经过点 、 ,与 轴交于点 ,过点 作 ,垂足为 , 的延长线交 轴于点 ,
(1)、求 的长度(结果保留根号);(2)、求拉杆端点 到水平滑杆 的距离(结果保留根号).20. 如图, 中, , , 平分 ,交 轴于点 ,点 是 轴上一点, 经过点 、 ,与 轴交于点 ,过点 作 ,垂足为 , 的延长线交 轴于点 , (1)、求证: 为 的切线;(2)、求 的半径.21. 有这样一个问题,如图1,在等边 中, , 为 的中点, , 分别是边 , 上的动点,且 ,若 ,试求 的长.爱钻研的小峰同学发现,可以通过几何与函数相结合的方法来解决这个问题,下面是他的探究思路,请帮他补充完整.
(1)、求证: 为 的切线;(2)、求 的半径.21. 有这样一个问题,如图1,在等边 中, , 为 的中点, , 分别是边 , 上的动点,且 ,若 ,试求 的长.爱钻研的小峰同学发现,可以通过几何与函数相结合的方法来解决这个问题,下面是他的探究思路,请帮他补充完整.
 (1)、注意到 为等边三角形,且 ,可得 ,于是可证 ,进而可得 ,注意到 为 中点, ,因此 和 满足的等量关系为.(2)、设 , ,则 的取值范围是.结合(1)中的关系求 与 的函数关系.(3)、在平面直角坐标系 中,根据已有的经验画出 与 的函数图象,请在图2中完成画图.(4)、回到原问题,要使 ,即为 ,利用(3)中的图象,通过测量,可以得到原问题的近似解为 (精确到0.1)22. 如图,在 中, , 是 边上的高, 是 边上的一个动点(不与 , 重合), , ,垂足分别为 , .
(1)、注意到 为等边三角形,且 ,可得 ,于是可证 ,进而可得 ,注意到 为 中点, ,因此 和 满足的等量关系为.(2)、设 , ,则 的取值范围是.结合(1)中的关系求 与 的函数关系.(3)、在平面直角坐标系 中,根据已有的经验画出 与 的函数图象,请在图2中完成画图.(4)、回到原问题,要使 ,即为 ,利用(3)中的图象,通过测量,可以得到原问题的近似解为 (精确到0.1)22. 如图,在 中, , 是 边上的高, 是 边上的一个动点(不与 , 重合), , ,垂足分别为 , . (1)、求证: ;(2)、 与 是否垂直?若垂直,请给出证明,若不垂直,请说明理由.23. 2019年11月20日,“美丽玉环,文旦飘香”号冠名列车正式发车,为广大旅客带去“中国文旦之乡”的独特味道.根据市场调查,在文旦上市销售的30天中,其销售价格 (元公斤)与第 天之间满足函数 (其中 为正整数);销售量 (公斤)与第 天之间的函数关系如图所示,如果文旦上市期间每天的其他费用为100元.
(1)、求证: ;(2)、 与 是否垂直?若垂直,请给出证明,若不垂直,请说明理由.23. 2019年11月20日,“美丽玉环,文旦飘香”号冠名列车正式发车,为广大旅客带去“中国文旦之乡”的独特味道.根据市场调查,在文旦上市销售的30天中,其销售价格 (元公斤)与第 天之间满足函数 (其中 为正整数);销售量 (公斤)与第 天之间的函数关系如图所示,如果文旦上市期间每天的其他费用为100元. (1)、求销售量 与第 天之间的函数关系式;(2)、求在文旦上市销售的30天中,每天的销售利润 与第 天之间的函数关系式;(日销售利润=日销售额-日维护费)(3)、求日销售利润 的最大值及相应的 的值.24. 定义:如果三角形的两个内角 与 满足 ,那么称这样的三角形为“类直角三角形”.
(1)、求销售量 与第 天之间的函数关系式;(2)、求在文旦上市销售的30天中,每天的销售利润 与第 天之间的函数关系式;(日销售利润=日销售额-日维护费)(3)、求日销售利润 的最大值及相应的 的值.24. 定义:如果三角形的两个内角 与 满足 ,那么称这样的三角形为“类直角三角形”.尝试运用
(1)、如图1,在 中, , , , 是 的平分线.
①证明 是“类直角三角形”;
②试问在边 上是否存在点 (异于点 ),使得 也是“类直角三角形”?若存在,请求出 的长;若不存在,请说明理由.
类比拓展
(2)、如图2, 内接于 ,直径 ,弦 ,点 是弧 上一动点(包括端点 , ),延长 至点 ,连结 ,且 ,当 是“类直角三角形”时,求 的长.