浙江省台州市路桥区2020届九年级上学期数学期末考试试卷

试卷更新日期：2020-03-27 类型：期末考试

进入出卷网下载

一、单选题

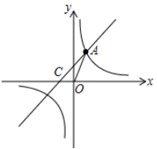
1. 下列方程中，为一元二次方程的是（）

A、x=2 B、x+y=3 C、 $x^{2} - 2 x = 4$ D、 $\frac{1}{x} = 2$

查看试题解析
2. 下列事件中，为必然事件的是（）

A、太阳从东方升起 B、发射一枚导弹，未击中目标 C、购买一张彩票，中奖 D、随机翻到书本某页，页码恰好是奇数

查看试题解析
3. 反比例函数 $y = - \frac{4}{x}$ （x＜0）如图所示，则矩形OAPB的面积是（）

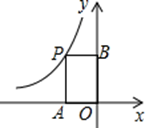A、-4 B、-2 C、2 D、4

查看试题解析
4. 如图，点A，B，C都在⊙O上，若∠C=30°，则∠AOB的度数为（）

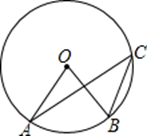A、30° B、60° C、150° D、120°

查看试题解析
5. 如图，在Rt△ABC中，∠BAC=90°，将Rt△ABC绕点C按逆时针方向旋转46°得到Rt△A′B′C，点A在边B′C上，则∠ACB的大小为（）

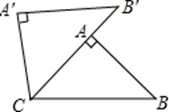A、23° B、44° C、46° D、54°

查看试题解析
6. 一件商品的原价是100元，经过两次降价后价格为81元，设每次降价的百分比都是x，根据题意，下面列出的方程正确的是（）

A、 $100 {(1 + x)}^{2} = 81$ B、 $100 {(1 - x)}^{2} = 81$ C、 $100 (1 + x) = 81$ D、 $100 (1 - x) = 81$

查看试题解析
7. 已知圆锥的底面半径为3cm，母线长为5cm，则圆锥的侧面积是（）

A、 $12 π {cm}^{2}$ B、 $15 π {cm}^{2}$ C、 $20 π {cm}^{2}$ D、 $30 π {cm}^{2}$

查看试题解析
8. 将二次函数y=2x²-4x+4的图象向左平移2个单位，再向下平移1个单位后所得图象的函数解析式为（）

A、y=2(x+1)²+1 B、y=2(x+1)²+3 C、y=2(x-3)²+1 D、y=-2(x-3)²+3

查看试题解析
9. 将半径为5cm的圆形纸片沿着弦AB进行翻折，弦AB的中点与圆心O所在的直线与翻折后的劣弧相交于C点，若OC=3cm，则折痕AB的长是（）

A、 $4 \sqrt{6} cm$ B、 $6 cm$ C、4cm或6cm D、 $4 \sqrt{6} cm$ 或 $6 cm$

查看试题解析
10. 如图，已知点A，B，C，D，E，F是边长为1的正六边形的顶点，连接任意两点均可得到一条线段，在连接两点所得的所有线段中任取一条线段，取到长度为2的线段的概率为（）

A、 $\frac{2}{3}$ B、 $\frac{2}{5}$ C、 $\frac{1}{3}$ D、 $\frac{1}{5}$

查看试题解析

二、填空题

11. 若点P(3，1)与点Q关于原点对称，则点Q的坐标是.

查看试题解析
12. 若反比例函数的图象在每一象限内，y随x的增大而增大，请写出满足条件的一个反比例函数的解折式.

查看试题解析
13. 若关于x的一元二次方程 $x^{2} - x + \frac{1}{4} m - 2 = 0$ 有实数根，则m的取值范围是.

查看试题解析

14. 在一个不透明的盒子里装有黑、白两种颜色的球共50只，这些球除颜色外其余完全相同.随机摸出一只球记下颜色后放回，不断重复上述实验，统计数据如下：

摸球的次数n	100	200	300	500	800	1000	3000
摸到白球的次数m	65	124	178	302	481	599	1803
摸到白球的频率 $\frac{n}{m}$	0.65	0.62	0.593	0.604	0.601	0.599	0.601

共有白球只.

查看试题解析

15. 如图，等边 $ΔABC$ 边长为2，分别以A，B，C为圆心，2为半径作圆弧，这三段圆弧围成的图形就是著名的等宽曲线——鲁列斯三角形，则该鲁列斯三角形的面积为.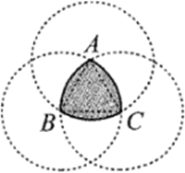

查看试题解析
16. 对于实数a和b，定义一种新的运算“*”， $a*b = {\begin{array}{l} b^{2} - ab ， a < b \\ - a^{2} + 2 ab - 1 ， a \geq b \end{array}$ ，计算 $(2 x + 1) * (x + 1)$ =.若 $(2 x + 1) * (x + 1) = m$ 恰有三个不相等的实数根 $x_{1} ， x_{2} ， x_{3}$ ，记 $k = x_{1} + x_{2} + x_{3}$ ，则k的取值范围是 .

查看试题解析

三、解答题

17. 解方程：

(1)、 $x^{2} - 2 x = 0$

(2)、 $x^{2} + 3 x + 1 = 0$

查看试题解析
18. 如图，已知点 $A (1 ， a)$ 在反比例函数 $y = \frac{2}{x}$ 的图像上.

(1)、求a的值；

(2)、如果直线y=x+b也经过点A，且与x轴交于点C，连接AO，求 $ΔAOC$ 的面积.

查看试题解析
19. 如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A(-2，3)，B(-4，1)，C(-1，2).

(1)、画出以点O为旋转中心，将△ABC顺时针旋转90°得到△A'B'C'

(2)、求点C在旋转过程中所经过的路径的长.

查看试题解析
20. 如图，已知AB为⊙O的直径，PA与⊙O相切于A点，点C是⊙O上的一点，且PC=PA.

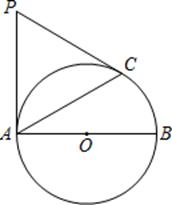(1)、求证：PC是⊙O的切线；

(2)、若∠BAC=45°，AB=4，求PC的长.

查看试题解析
21. 为了“创建文明城市，建设美丽台州”，我市某社区将辖区内一块不超过1000平方米的区域进行美化.经调查，美化面积为100平方米时，每平方米的费用为300元.每增加1平方米，每平方米的费用下降0.2元。设美化面积增加x平方米，美化所需总费用为y元.

(1)、求y与x的函数关系式；

(2)、当美化面积增加100平方米时，美化的总费用为多少元；

(3)、当美化面积增加多少平方米时，美化所需费用最高?最高费用是多少元?

查看试题解析
22. 如图，在 $ΔABC$ 中， $∠ ACB = 90^{\circ}$ ，点P为 $ΔABC$ 内一点，连接PA，PB，PC，求PA+PB+PC的最小值，小华的解题思路，以点A为旋转中心，将 $ΔAPB$ 顺时针旋转 $60^{\circ}$ 得到 $ΔAMN$ ，那么就将求PA+PB+PC的值转化为求PM+MN+PC的值，连接CN，当点P，M落在CN上时，此题可解.

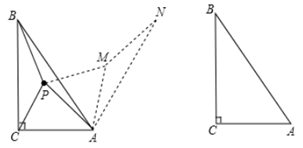(1)、请判断 $ΔAPM$ 的形状，并说明理由；

(2)、请你参考小华的解题思路，证明PA+PB+PC=PM+MN+PC；

(3)、当 $AC = BC = 2$ ，求PA+PB+PC的最小值.

查看试题解析
23. （定义）在平面直角坐标系中，对于函数图象的横宽、纵高给出如下定义：当自变量x在 $a \leq x \leq b$ 范围内时，函数值y满足 $c \leq y \leq d$ .那么我们称b-a为这段函数图象的横宽，称d-c为这段函数图象的纵高.纵高与横宽的比值记为k即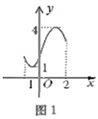： $k = \frac{d - c}{b - a}$ .

（示例）如图1，当 $- 1 \leq x \leq 2$ 时；函数值y满足 $1 \leq y \leq 4$ ，那么该段函数图象的横宽为2-（-1）=3，纵高为4-1=3.则 $k = \frac{3}{3} = 1$ .

（应用）

(1)、当 $1 \leq x \leq 3$ 时，函数 $y = - 2 x + 4$ 的图象横宽为，纵高为；

(2)、已知反比例函数 $y = \frac{n}{x} (n > 0)$ ，当点M(3，4)和点N在该函数图象上，且MN段函数图象的纵高为2时，求k的值.

(3)、已知二次函数 $y = - {mx}^{2} + 4 mx$ 的图象与x轴交于A点，B点.
①若m=1，是否存在这样的抛物线段，当 $a \leq x \leq b$ ( $a \neq b$ )时，函数值满足 $2 a \leq y \leq 3 b$ 若存在，请求出这段函数图象的k值；若不存在，请说明理由.

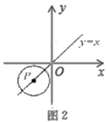
②如图2，若点P在直线y=x上运动，以点P为圆心， $3 \sqrt{2}$ 为半径作圆，当AB段函数图象的k=1时，抛物线顶点恰好落在 $⊙ P$ 上，请直接写出此时点P的坐标.

查看试题解析