吉林省长春市2020届高三文数一模试卷

试卷更新日期：2020-03-27 类型：高考模拟

进入出卷网下载

一、单选题

1. 复数 $z = - 2 + i$ ，则它的共轭复数 $\bar{z}$ 在复平面内对应的点位于（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
2. 已知集合 $A = {x | x \geq 2 ，或 x \leq - 2}$ ， $B = {x | x^{2} - 3 x > 0}$ ，则 $A \cap B =$ （）

A、 $\emptyset$ B、 ${x | x > 3 ，$ 或 $x$ ≤ $- 2}$ C、 ${x | x > 3 ，$ 或 $x < 0}$ D、 ${x | x > 3 ，$ 或 $x \leq 2}$

查看试题解析
3. 已知等差数列 ${a_{n}}$ 的前 $n$ 项和为 $S_{n}$ ， $S_{5} = 15$ ， $a_{4} = 5$ ，则 $S_{9} =$ （）

A、 $45$ B、 $63$ C、 $54$ D、 $81$

查看试题解析
4. 已知条件 $p ： x > 1$ ，条件 $q ： x \geq 2$ ，则 $p$ 是 $q$ 的（）

A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件

查看试题解析
5. 2019年是新中国成立七十周年，新中国成立以来，我国文化事业得到了充分发展，尤其是党的十八大以来，文化事业发展更加迅速，下图是从2013 年到 2018 年六年间我国公共图书馆业机构数（个）与对应年份编号的散点图（为便于计算，将 2013 年编号为 1，2014 年编号为 2，…，2018年编号为 6，把每年的公共图书馆业机构个数作为因变量，把年份编号从 1 到 6 作为自变量进行回归分析），得到回归直线 $\hat{y} = 13.743 x + 3095.7$ ，其相关指数 $R^{2} = 0.9817$ ，给出下列结论，其中正确的个数是（）

①公共图书馆业机构数与年份的正相关性较强 ②公共图书馆业机构数平均每年增加13.743个 ③可预测 2019 年公共图书馆业机构数约为3192个

A、0 B、1 C、2 D、3

查看试题解析
6. 已知直线 $x + y = 0$ 与圆 ${(x - 1)}^{2} + {(y - b)}^{2} = 2$ 相切，则 $b =$ （）

A、 $- 3$ B、 $1$ C、 $- 3$ 或 $1$ D、 $\frac{5}{2}$

查看试题解析
7. 已知 $a = {(\frac{1}{3})}^{3}$ ， $b = 3^{\frac{1}{3}}$ ， $c = \log_{\frac{1}{3}} 3$ ，则（）

A、 $a < b < c$ B、 $c < b < a$ C、 $c < a < b$ D、 $b < c < a$

查看试题解析
8. 已知 $a ， b ， c$ 为直线， $α ， β ， γ$ 平面，则下列说法正确的是（）
① $a ⊥ α ， b ⊥ α$ ，则 $a / / b$ ② $α ⊥ γ ， β ⊥ γ$ ，则 $α ⊥ β$ ③ $a / / α ， b / / α$ ，则 $a / / b$ ④ $α ∥ γ ， β ∥ γ$ ，则 $α / / β$

A、①②③ B、②③④ C、①③ D、①④

查看试题解析
9. 函数 $y = 2 \sin (ω x + φ)$ $(ω > 0 ， | φ | < \frac{π}{2})$ 的图象（部分图象如图所示），则其解析式为（）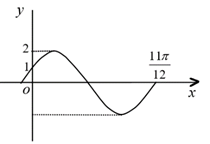

A、 $f (x) = 2 \sin (2 x + \frac{π}{6})$ B、 $f (x) = 2 \sin (x + \frac{π}{6})$ C、 $f (x) = 2 \sin (4 x + \frac{π}{6})$ D、 $f (x) = 2 \sin (x - \frac{π}{6})$

查看试题解析
10. 中国传统扇文化有着极其深厚的底蕴. 一般情况下，折扇可看作是从一个圆面中剪下的扇形制作而成，设扇形的面积为 $S_{1}$ ，圆面中剩余部分的面积为 $S_{2}$ ，当 $S_{1}$ 与 $S_{2}$ 的比值为 $\frac{\sqrt{5} - 1}{2}$ 时，扇面看上去形状较为美观，那么此时扇形的圆心角的弧度数为（）

A、 $(3 - \sqrt{5}) π$ B、 $(\sqrt{5} - 1) π$ C、 $(\sqrt{5} + 1) π$ D、 $(\sqrt{5} - 2) π$

查看试题解析
11. 已知 $F$ 是抛物线 $y^{2} = 4 x$ 的焦点，则过 $F$ 作倾斜角为 $60 °$ 的直线分别交抛物线于 $A ， B$ （ $A$ 在 $x$ 轴上方）两点，则 $\frac{| A F |}{| B F |}$ 的值为（）

A、 $\sqrt{3}$ B、 $2$ C、 $3$ D、 $4$

查看试题解析
12. 已知函数 $f (x) = {\begin{array}{l} e^{- x} - 1 (x \leq 0) \\ \sqrt{x} (x > 0) \end{array}$ ，若存在 $x_{0} \in R$ 使得 $f (x_{0}) \leq m (x_{0} - 1) - 1$ 成立，则实数 $m$ 的取值范围为（）

A、 $(0 ， + \infty)$ B、 $[- 1 ， 0) \cup (0 ， + \infty)$ C、 $(- \infty ， - 1] \cup [1 ， + \infty)$ D、 $(- \infty ， - 1] \cup (0 ， + \infty)$

查看试题解析

二、填空题

13. 已知 $\sin \frac{α}{2} - \cos \frac{α}{2} = \frac{1}{5}$ ，则 $\sin α =$ .

查看试题解析
14. 设变量 $x ， y$ 满足约束条件 ${\begin{array}{l} x - y \leq 0 \\ x + 3 y \leq 4 \\ x + 2 \geq 0 \end{array}$ ，则 $z = x - 3 y$ 的最小值等于.

查看试题解析
15. 三棱锥 $P - A B C$ 中， $P A$ ⊥平面 $A B C$ ， $A B ⊥ A C$ , $P A = \sqrt{10}$ , $A B = 2, A C = \sqrt{2}$ ，则三棱锥 $P - A B C$ 的外接球的表面积为.

查看试题解析
16. 已知△ $A B C$ 的内角 $A, B, C$ 的对边分别为 $a, b, c$ ，若 $\overset{⇀}{m} = (b - c, a - b)$ , $\overset{⇀}{n} = (\sin C, \sin A + \sin B)$ ，且 $\overset{⇀}{m} ⊥ \overset{⇀}{n}$ ，则 $A =$ ;若△ $A B C$ 的面积为 $\sqrt{3}$ ，则△ $A B C$ 的周长的最小值为.

查看试题解析

三、解答题

17. 已知数列 ${a_{n}}$ 中， $a_{1} = 2$ ， $a_{n + 1} = 2 a_{n} + 2^{n + 1}$ ，设 $b_{n} = \frac{a_{n}}{2^{n}}$ .
（Ⅰ）求证：数列 ${b_{n}}$ 是等差数列；

（Ⅱ）求数列 ${\frac{1}{b_{n} b_{n + 1}}}$ 的前 $n$ 项和 $S_{n}$ .

查看试题解析
18. 环保部门要对所有的新车模型进行广泛测试，以确定它的行车里程的等级，右表是对 100 辆新车模型在一个耗油单位内行车里程（单位：公里）的测试结果.

（Ⅰ）做出上述测试结果的频率分布直方图，并指出其中位数落在哪一组；

（Ⅱ）用分层抽样的方法从行车里程在区间[38，40)与[40，42)的新车模型中任取5辆，并从这5辆中随机抽取2辆，求其中恰有一个新车模型行车里程在[40，42)内的概率.

查看试题解析
19. 在三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，平面 $A B C$ 、平面 $A C C_{1} A_{}$ 、平面 $B C C_{1} B_{1}$ 两两垂直.

（Ⅰ）求证： $C A ， C B ， C C_{1}$ 两两垂直；

（Ⅱ）若 $C A = C B = C C_{1} = a$ ，求三棱锥 $B_{1} - A_{1} B C$ 的体积.

查看试题解析
20. 已知点 $M (- 1, 0), N (1, 0)$ ，若点 $P (x, y)$ 满足 $| P M | + | P N | = 4$ .
（Ⅰ）求点 $P$ 的轨迹方程；

（Ⅱ）过点 $Q (- \sqrt{3}, 0)$ 的直线 $l$ 与（Ⅰ）中曲线相交于 $A, B$ 两点， $O$ 为坐标原点，求△ $A O B$ 面积的最大值及此时直线 $l$ 的方程.

查看试题解析
21. 设函数 $f (x) = \ln x + \frac{x + 1}{x}$ .
（Ⅰ）求函数 $f (x)$ 的极值；

（Ⅱ）若 $x \in (0 ， 1)$ 时，不等式 $\frac{1 + x}{a (1 - x)} \ln x < - 2$ 恒成立，求实数 $a$ 的取值范围.

查看试题解析
22. 在平面直角坐标系 $x O y$ 中，直线 $l$ 的参数方程为 ${\begin{array}{l} x = 1 - \frac{\sqrt{2}}{2} t \\ y = 2 + \frac{\sqrt{2}}{2} t \end{array}$ （ $t$ 为参数），以坐标原点 $O$ 为极点， $x$ 轴的正半轴为极轴建立极坐标系，圆 $C$ 的极坐标方程为 $ρ^{2} - 4 ρ \cos θ = 3$ .
（Ⅰ）求直线 $l$ 的普通方程和圆 $C$ 的直角坐标方程；

（Ⅱ）直线 $l$ 与圆 $C$ 交于 $A, B$ 两点，点 $P (1, 2)$ ，求 $| P A | \cdot | P B |$ 的值.

查看试题解析
23. 已知函数 $f (x) = | x + 3 | - | x - 1 |$ .
（Ⅰ）解关于 $x$ 的不等式 $f (x) \geq x + 1$ ；

（Ⅱ）若函数 $f (x)$ 的最大值为 $M$ ，设 $a > 0, b > 0$ ，且 $(a + 1) (b + 1) = M$ ，求 $a + b$ 的最小值.

查看试题解析