浙江省绍兴市诸暨市2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-03-27 类型:期末考试
一、单选题
-
1. 抛物线 的对称轴为直线( )A、 B、 C、 D、2. 如图,已知 中, , , ,则 的值为( )
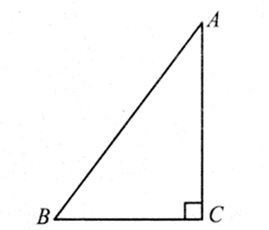 A、 B、 C、 D、3. 在一个不透明的盒子中装有2个白球,若干个黄球,它们除了颜色不同外,其余均相同.若从中随机摸出一个白球的概率是 ,则黄球的个数为( )A、2 B、3 C、4 D、64. 若两个相似三角形的周长之比为1∶4,则它们的面积之比为( )A、1∶2 B、1∶4 C、1∶8 D、1∶165. 用直角三角板检查半圆形的工件,下列工件合格的是( )A、
A、 B、 C、 D、3. 在一个不透明的盒子中装有2个白球,若干个黄球,它们除了颜色不同外,其余均相同.若从中随机摸出一个白球的概率是 ,则黄球的个数为( )A、2 B、3 C、4 D、64. 若两个相似三角形的周长之比为1∶4,则它们的面积之比为( )A、1∶2 B、1∶4 C、1∶8 D、1∶165. 用直角三角板检查半圆形的工件,下列工件合格的是( )A、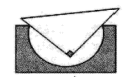 B、
B、 C、
C、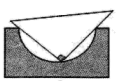 D、
D、 6. 将抛物线y=(x﹣2)2﹣8向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为( )A、y=(x+1)2﹣13 B、y=(x﹣5)2﹣3 C、y=(x﹣5)2﹣13 D、y=(x+1)2﹣37. 如图, 是圆内接四边形 的一条对角线,点 关于 的对称点 在边 上,连接 .若 ,则 的度数为( )
6. 将抛物线y=(x﹣2)2﹣8向左平移3个单位,再向上平移5个单位,得到抛物线的表达式为( )A、y=(x+1)2﹣13 B、y=(x﹣5)2﹣3 C、y=(x﹣5)2﹣13 D、y=(x+1)2﹣37. 如图, 是圆内接四边形 的一条对角线,点 关于 的对称点 在边 上,连接 .若 ,则 的度数为( )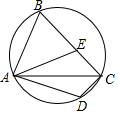 A、106° B、116° C、126° D、136°8. 如图,△ABC中,点D是AB的中点,点E是AC边上的动点,若△ADE与△ABC相似,则下列结论一定成立的是( )
A、106° B、116° C、126° D、136°8. 如图,△ABC中,点D是AB的中点,点E是AC边上的动点,若△ADE与△ABC相似,则下列结论一定成立的是( )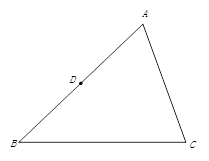 A、E为AC的中点 B、DE是中位线或AD·AC=AE·AB C、∠ADE=∠C D、DE∥BC或∠BDE+∠C=180°9. 如图所示为两把按不同比例尺进行刻度的直尺,每把直尺的刻度都是均匀的,已知两把直尺在刻度10处是对齐的,且上面的直尺在刻度15处与下面的直尺在刻度18处也刚好对齐,则上面直尺的刻度16与下面直尺对应的刻度是( )
A、E为AC的中点 B、DE是中位线或AD·AC=AE·AB C、∠ADE=∠C D、DE∥BC或∠BDE+∠C=180°9. 如图所示为两把按不同比例尺进行刻度的直尺,每把直尺的刻度都是均匀的,已知两把直尺在刻度10处是对齐的,且上面的直尺在刻度15处与下面的直尺在刻度18处也刚好对齐,则上面直尺的刻度16与下面直尺对应的刻度是( )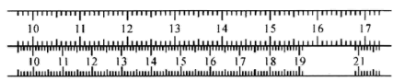 A、19.4 B、19.5 C、19.6 D、19.710. 学校体育室里有6个箱子,分别装有篮球和足球(不混装),数量分别是8,9,16,20,22,27,体育课上,某班体育委员拿走了一箱篮球,在剩下的五箱球中,足球的数量是篮球的2倍,则这六箱球中,篮球有( )箱.A、2 B、3 C、4 D、5
A、19.4 B、19.5 C、19.6 D、19.710. 学校体育室里有6个箱子,分别装有篮球和足球(不混装),数量分别是8,9,16,20,22,27,体育课上,某班体育委员拿走了一箱篮球,在剩下的五箱球中,足球的数量是篮球的2倍,则这六箱球中,篮球有( )箱.A、2 B、3 C、4 D、5二、填空题
-
11. 若 = ,则 的值为.12. 如图, 与⊙ 相切于点 , , ,则⊙ 的半径为 .
 13. 已知线段 ,点 是它的黄金分割点, ,设以 为边的正方形的面积为 ,以 为邻边的矩形的面积为 ,则 与 的关系是.14. 将6×4的正方形网格如图所示放置在平面直角坐标系中,每个小正方形的边长为1,若点 在第一象限内,且在正方形网格的格点上,若 是钝角 的外心,则 的坐标为.
13. 已知线段 ,点 是它的黄金分割点, ,设以 为边的正方形的面积为 ,以 为邻边的矩形的面积为 ,则 与 的关系是.14. 将6×4的正方形网格如图所示放置在平面直角坐标系中,每个小正方形的边长为1,若点 在第一象限内,且在正方形网格的格点上,若 是钝角 的外心,则 的坐标为.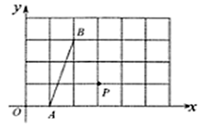 15. 如图,在半径为5的⊙ 中,弦 , 是弦 所对的优弧上的动点,连接 ,过点 作 的垂线交射线 于点 ,当 是以 为腰的等腰三角形时,线段 的长为.
15. 如图,在半径为5的⊙ 中,弦 , 是弦 所对的优弧上的动点,连接 ,过点 作 的垂线交射线 于点 ,当 是以 为腰的等腰三角形时,线段 的长为.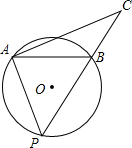 16. 如图,平行四边形 中, , , ,点E在AD上,且AE=4,点 是AB上一点,连接EF,将线段EF 绕点E逆时针旋转120°得到EG,连接DG,则线段DG的最小值为.
16. 如图,平行四边形 中, , , ,点E在AD上,且AE=4,点 是AB上一点,连接EF,将线段EF 绕点E逆时针旋转120°得到EG,连接DG,则线段DG的最小值为.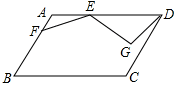
三、解答题
-
17. 计算:18. 为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.(1)、八(1)班抽中歌曲《我和我的祖国》的概率是;(2)、试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.19. 商场销售某种冰箱,该种冰箱每台进价为2500元,已知原销售价为每台2900元时,平均每天能售出8台.若在原销售价的基础上每台降价50元,则平均每天可多售出4台.设每台冰箱的实际售价比原销售价降低了 元.(1)、填表:
每天的销售量/台
每台销售利润/元
降价前
8
400
降价后
(2)、商场为使这种冰箱平均每天的销售利润达到最大时,则每台冰箱的实际售价应定为多少元?20. 某课桌生产厂家研究发现,倾斜12°至24°的桌面有利于学生保持躯体自然姿势.根据这一研究,厂家决定将水平桌面做成可调节角度得桌面.新桌面的设计图如图1, 可绕点 旋转,在点 处安装一根长度一定且 处固定,可旋转的支撑臂 , .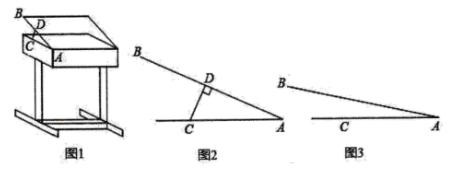
(参考数据: , , , )
(1)、如图2,当 时, ,求支撑臂 的长;(2)、如图3,当 时,求 的长.(结果保留根号)21. 如图, 是⊙ 的直径, 是 的中点,弦 于点 ,过点 作 交 的延长线于点 .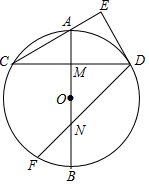 (1)、连接 ,求 ;(2)、点 在 上, ,DF交 于点 .若 ,求 的长.22. 锐角 中, , 为 边上的高线, ,两动点 分别在边 上滑动,且 ,以 为边向下作正方形 (如图1),设其边长为 .
(1)、连接 ,求 ;(2)、点 在 上, ,DF交 于点 .若 ,求 的长.22. 锐角 中, , 为 边上的高线, ,两动点 分别在边 上滑动,且 ,以 为边向下作正方形 (如图1),设其边长为 .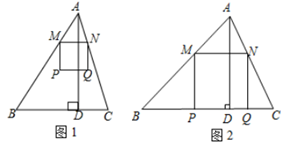 (1)、当 恰好落在边 上(如图2)时,求 ;(2)、正方形 与 公共部分的面积为 时,求 的值.23. 定义:已知点 是三角形边上的一点(顶点除外),若它到三角形一条边的距离等于它到三角形的一个顶点的距离,则我们把点 叫做该三角形的等距点.
(1)、当 恰好落在边 上(如图2)时,求 ;(2)、正方形 与 公共部分的面积为 时,求 的值.23. 定义:已知点 是三角形边上的一点(顶点除外),若它到三角形一条边的距离等于它到三角形的一个顶点的距离,则我们把点 叫做该三角形的等距点.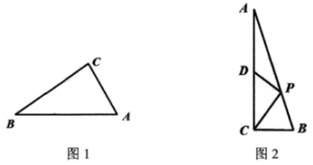 (1)、如图1: 中, , , , 在斜边 上,且点 是 的等距点,试求 的长;(2)、如图2, 中, ,点 在边 上, , 为 中点,且 .
(1)、如图1: 中, , , , 在斜边 上,且点 是 的等距点,试求 的长;(2)、如图2, 中, ,点 在边 上, , 为 中点,且 .①求证: 的外接圆圆心是 的等距点;②求 的值.
24. 如图,已知直线 与抛物线 相交于 , 两点,抛物线 交 轴于点 ,交 轴正半轴于 点,抛物线的顶点为 . (1)、求抛物线的解析式;(2)、设点 为直线 下方的抛物线上一动点,当 的面积最大时,求 的面积及点 的坐标;(3)、若点 为 轴上一动点,点 在抛物线上且位于其对称轴右侧,当 与 相似时,求 点的坐标.
(1)、求抛物线的解析式;(2)、设点 为直线 下方的抛物线上一动点,当 的面积最大时,求 的面积及点 的坐标;(3)、若点 为 轴上一动点,点 在抛物线上且位于其对称轴右侧,当 与 相似时,求 点的坐标.