浙江省绍兴市新昌县2020届九年级上学期数学期末考试试卷

试卷更新日期：2020-03-27 类型：期末考试

进入出卷网下载

一、单选题

1. 二次函数 $y = - {(x + 2)}^{2} + 6$ 图象的顶点坐标是（）

A、 $(2 ， 6)$ B、 $(- 2 ， 6)$ C、 $(2 ， - 6)$ D、 $(- 2 ， - 6)$

查看试题解析
2. 一个布袋里装有3个红球、2个白球，每个球除颜色外均相同，从中任意摸出一个球，则摸出的球是红球的概率是（）

A、 $\frac{1}{5}$ B、 $\frac{2}{5}$ C、 $\frac{3}{5}$ D、 $\frac{2}{3}$

查看试题解析
3. 已知⊙O的半径为3，直线l与⊙O相交，则圆心O到直线l的距离d的取值范围是（）

A、d＝3 B、d＞3 C、0≤d＜3 D、d＜3

查看试题解析
4. 在△ABC中，∠C=90°，AC=8，BC=6，则sinB的值是（　　）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{4}{3}$ D、 $\frac{3}{4}$

查看试题解析
5. 如图，⊙O的直径CD⊥AB，∠AOC=50°，则∠CDB大小为（）

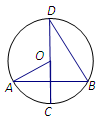A、25° B、30° C、40° D、50°

查看试题解析
6. 如图，在△ABC中，EG∥BC，若 $\frac{E G}{B C} = \frac{1}{3}$ ，则 $\frac{A F}{A D}$ 的值为（）

A、 $\frac{1}{2}$ B、 $\frac{2}{3}$ C、 $\frac{1}{4}$ D、 $\frac{1}{3}$

查看试题解析
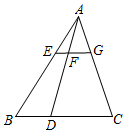7. 把抛物线y=﹣2x²+4x+1的图象向左平移2个单位，再向上平移3个单位，所得的抛物线的函数关系式是（）

A、y=﹣2（x﹣1）²+6 B、y=﹣2（x﹣1）²﹣6 C、y=﹣2（x+1）²+6 D、y=﹣2（x+1）²﹣6

查看试题解析
8. 如图，OT是Rt△ABO的斜边AB上的高线，OA＝OB，以O为圆心，OT为半径的圆交OA于点D，过点D作⊙O的切线CD，交AB于点C，已知OT＝2，则BC的长为（）

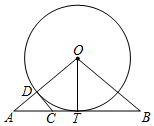A、2 B、2 $\sqrt{2}$ C、3 D、2+ $\sqrt{2}$

查看试题解析
9. 在平面直角坐标系中，把点P $(3 ， 4)$ 绕原点旋转90°得到点P₁ ，则点P₁的坐标是（）

A、 $(- 4 ， 3)$ B、 $(- 3 ， 4)$ C、 $(- 3 ， 4)$ 或 $(3 ， - 4)$ D、 $(- 4 ， 3)$ 或 $(4 ， - 3)$

查看试题解析
10. 如图，在平面直角坐标系中，正方形OABC的边长为4，把它内部及边上的横、纵坐标均为整数的点称为整点，点P为抛物线 $y = - {(x - m)}^{2} + m + 2$ 的顶点（m为整数），当点P在正方形OABC内部或边上时，抛物线下方（包括边界）的整点最少有（）

A、3个 B、5个 C、10个 D、15个

查看试题解析

二、填空题

11. 如果2a=3b，那么 $\frac{a}{b} =$ .

查看试题解析
12. 如图，为了美化校园，学校在一块靠墙角的空地上建造了一个扇形花圃，扇形的圆心角∠AOB＝120°，半径为9m，则扇形的弧长是m.

查看试题解析
13. 小李与小陈做猜拳游戏，规定每人每次出一只手，且至少要出一个手指，两人出拳的手指数之和为偶数时小李获胜，那么（填“小李”或“小陈”）获胜的可能性较大.

查看试题解析
14. 如图，在圆内接四边形ABCD中，∠C＝2∠A，则cosA＝.

查看试题解析
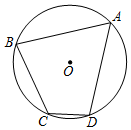15. 抛物线y＝ax²+c（a≠0）与直线y＝6相交于点A，B，与y轴交于点C $(0 ， - 2)$ ，且∠ACB为直角，当y＜0时，自变量x的取值范围是.

查看试题解析
16. 如图，在矩形ABCD中，AB＝6，AD＝8，点M，N分别为AD，AC上的动点（不含端点），AN＝DM，连结点M与矩形的一个顶点，以该线段为直径作⊙O，当点N和矩形的另一个顶点也在⊙O上时，线段DM的长为.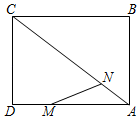

查看试题解析

三、解答题

17. 计算：

(1)、4sin²60°﹣2+tan45°；

(2)、已知线段a＝2，b＝8，求a，b的比例中项线段.

查看试题解析
18. 如图，在Rt△ABC中，∠C＝90°.

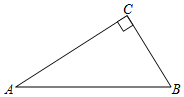(1)、请用直尺和圆规作出Rt△ABC的外接圆，圆心为O（保留作图痕迹，不要求写作法）；

(2)、若AB＝6，∠A＝30°，请求出扇形AOC的面积.

查看试题解析
19. 某商场开业，为了活跃气氛，用红、黄、蓝三色均分的转盘设计了两种抽奖方案，凡来商场消费的顾客都可以选择一种抽奖方案进行抽奖.
方案一：转动转盘一次，指针落在红色区域可领取一份奖品；

方案二：转动转盘两次，指针落在不同颜色区域可领取一份奖品，你会选择哪个方案？请用相关的数学知识说明理由.

查看试题解析
20. 如图，某次台风来袭时，垂直于地面的大树AB被刮倾斜30°后，折断倒在地上，树的顶部恰好落在地面上点D处，大树被折断部分和地面所成的角∠ADC＝45°，AD＝4米，求这棵大树AB原来的高度是多少米？（结果精确到个位，参考数据： $\sqrt{2} \approx 1.4$ ， $\sqrt{3} \approx 1.7$ ， $\sqrt{6} \approx 2.4$ ）

查看试题解析
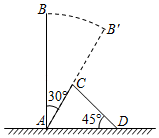21. 在△ABC中，AB＝6，BC＝5，AC＝4，D是线段AB上一点，且DB＝4，过点D作DE与线段AC相交于点E，使以A，D，E为顶点的三角形与△ABC相似，求DE的长.请根据下列两位同学的交流回答问题：

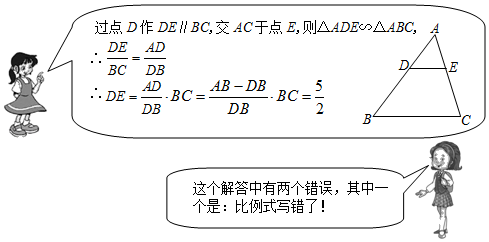(1)、写出正确的比例式及后续解答；

(2)、指出另一个错误，并给予正确解答.

查看试题解析
22. 定义：同时经过x轴上两点A $(m ， 0)$ ，B $(n ， 0)$ （m≠n）的两条抛物线称为同弦抛物线.如抛物线C₁： $y = (x - 1) (x - 3)$ 与抛物线C₂： $y = 2 (x - 1) (x - 3)$ 是都经过 $(1 ， 0)$ ， $(3 ， 0)$ 的同弦抛物线.

(1)、引进一个字母，表达出抛物线C₁的所有同弦抛物线；

(2)、判断抛物线C₃： $y = \frac{1}{2} x^{2} - \frac{3}{2} x + 1$ 与抛物线C₁是否为同弦抛物线，并说明理由；

(3)、已知抛物线C₄是C₁的同弦抛物线，且过点 $(4 ， 5)$ ，求抛物线C对应函数的最大值或最小值.

查看试题解析
23. 如图，AB是⊙O的直径，D是⊙O上一点，DE⊥AB于点E，且∠ADE＝60°，C是 $\overset{⌢}{ABD}$ 上一点，连结AC，CD.

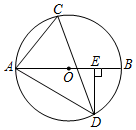(1)、求∠ACD的度数；

(2)、证明：AD²＝AB•AE；

(3)、如果AB＝8，∠ADC＝45°，请你编制一个计算题（不标注新的字母），并直接给出答案.（根据编出的问题层次，给不同的得分）

查看试题解析
24. 如图1是一块内置量角器的等腰直角三角板，它是一个轴对称图形.已知量角器所在的半圆O的直径DE与AB之间的距离为1，DE＝4，AB＝8，点N为半圆O上的一个动点，连结AN交半圆或直径DE于点M.

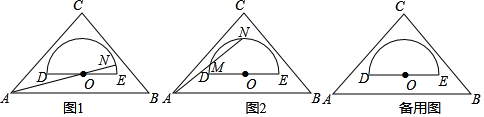(1)、当AN经过圆心O时，求AN的长；

(2)、如图2，若N为量角器上表示刻度为90°的点，求△MON的周长；

(3)、当 $\frac{A M}{A N} = \frac{1}{2}$ 时，求△MON的面积.

查看试题解析