浙江省湖州市德清县2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-03-27 类型:期末考试
一、单选题
-
1. 抛物线y=4x2﹣3的顶点坐标是( )A、(0,3) B、(0,﹣3) C、(﹣3,0) D、(4,﹣3)2. 下列各组中的四条线段成比例的是( )A、4cm,2cm,1cm,3cm B、1cm,2cm,3cm,5cm C、3cm,4cm,5cm,6cm D、1cm,2cm,2cm,4cm3. 如图,⊙O的半径为5,弦心距OC=3,则弦AB的长是( )
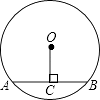 A、4 B、6 C、8 D、54. 在△ABC中,∠C=90°,AC=6,BC=8,则cosB的值是( )A、 B、 C、 D、5.
A、4 B、6 C、8 D、54. 在△ABC中,∠C=90°,AC=6,BC=8,则cosB的值是( )A、 B、 C、 D、5.如图,下列条件不能判定△ADB∽△ABC的是( )
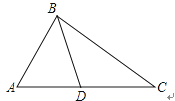 A、∠ABD=∠ACB B、∠ADB=∠ABC C、AB2=AD•AC D、6. 有四张背面一模一样的卡片,卡片正面分别写着一个函数关系式,分别是 ,将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是 随 的增大而增大的概率是( )A、 B、 C、 D、17. 如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )
A、∠ABD=∠ACB B、∠ADB=∠ABC C、AB2=AD•AC D、6. 有四张背面一模一样的卡片,卡片正面分别写着一个函数关系式,分别是 ,将卡片顺序打乱后,随意从中抽取一张,取出的卡片上的函数是 随 的增大而增大的概率是( )A、 B、 C、 D、17. 如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )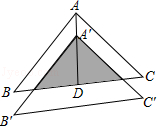 A、2 B、3 C、 D、8.
A、2 B、3 C、 D、8.如图,抛物线y=ax2+bx+c(a>0)的对称轴是直线x=1,且经过点P(3,0),则a-b+c的值为 ( )
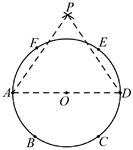
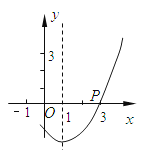 A、0 B、-1 C、1 D、29. 已知点A,B,C,D,E,F是半径为r的⊙O的六等分点,分别以A,D为圆心,AE和DF长为半径画圆弧交于点P.以下说法正确的是( )
A、0 B、-1 C、1 D、29. 已知点A,B,C,D,E,F是半径为r的⊙O的六等分点,分别以A,D为圆心,AE和DF长为半径画圆弧交于点P.以下说法正确的是( )①∠PAD=∠PDA=60º; ②△PAO≌△ADE;③PO= r;④AO∶OP∶PA=1∶ ∶ .
 A、①④ B、②③ C、③④ D、①③④10. 如图1,在菱形ABCD中,∠A=120°,点E是BC边的中点,点P是对角线BD上一动点,设PD的长度为x,PE与PC的长度和为y,图2是y关于x的函数图象,其中H是图象上的最低点,则a+b的值为( )
A、①④ B、②③ C、③④ D、①③④10. 如图1,在菱形ABCD中,∠A=120°,点E是BC边的中点,点P是对角线BD上一动点,设PD的长度为x,PE与PC的长度和为y,图2是y关于x的函数图象,其中H是图象上的最低点,则a+b的值为( )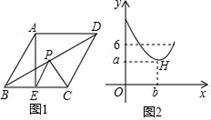 A、7 B、 C、 D、
A、7 B、 C、 D、二、填空题
-
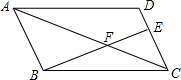
11. 一个不透明的布袋里装有100个只有颜色不同的球,这100个球中有m个红球 通过大量重复试验后发现,从布袋中随机摸出一个球摸到红球的频率稳定在 左右,则m的值约为.12. 抛物线y=3x2向右平移1个单位,再向下平移2个单位,所得到的抛物线是.13. 如果一个扇形的半径是1,弧长是 ,那么此扇形的圆心角的大小为度.14. 如图,在▱ABCD中,点E在DC边上,若 ,则 的值为.
 15. 如图,AB是⊙O的弦,AB=4,点C是⊙O上的一个动点,且∠ACB=45°.若点M,N分别是AB,BC的中点,则MN长的最大值是.
15. 如图,AB是⊙O的弦,AB=4,点C是⊙O上的一个动点,且∠ACB=45°.若点M,N分别是AB,BC的中点,则MN长的最大值是.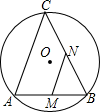 16. 定义:在平面直角坐标系中,我们将横、纵坐标都是整数的点称为“整点”.若抛物线y=ax2﹣2ax+a+3与x轴围成的区域内(不包括抛物线和x轴上的点)恰好有8个“整点”,则a的取值范围是.
16. 定义:在平面直角坐标系中,我们将横、纵坐标都是整数的点称为“整点”.若抛物线y=ax2﹣2ax+a+3与x轴围成的区域内(不包括抛物线和x轴上的点)恰好有8个“整点”,则a的取值范围是.三、解答题
-
17. 计算:2cos30°+ sin45°﹣tan260°.18. 已知:如图,在△ABC中,AD是∠BAC的平分线,∠ADE=∠B.
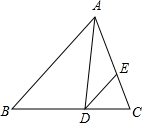
求证:
(1)、△ABD∽△ADE;(2)、AD2=AE•AB.19. 现如今,“垃圾分类”意识已深入人心,如图是生活中的四个不同的垃圾分类投放桶,分别写着:有害垃圾、厨余垃圾、其他垃圾、可回收垃圾.其中小明投放了一袋垃圾,小丽投放了两袋垃圾.
(1)、直接写出小明投放的垃圾恰好是“厨余垃圾”的概率;(2)、求小丽投放的两袋垃圾不同类的概率.
20. 某品牌太阳能热水器的实物图和横断面示意图如图所示.已知真空集热管DE与支架CB所在直线相交于点O,且 ;支架BC与水平线AD垂直. , , ,另一支架AB与水平线夹角 ,求OB的长度(结果精确到1cm;温馨提示: , , )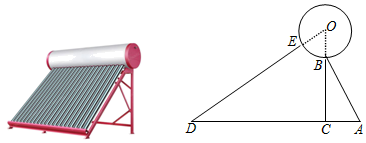 21. 如图,已知抛物线y=-x2+mx+3与x轴交于点A、B两点,与y轴交于C点,点B的坐标为(3,0),抛物线与直线y=- x+3交于C、D两点.连接BD、AD.
21. 如图,已知抛物线y=-x2+mx+3与x轴交于点A、B两点,与y轴交于C点,点B的坐标为(3,0),抛物线与直线y=- x+3交于C、D两点.连接BD、AD.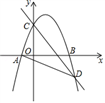 (1)、求m的值.(2)、抛物线上有一点P,满足S△ABP=4S△ABD , 求点P的坐标.22. 小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:
(1)、求m的值.(2)、抛物线上有一点P,满足S△ABP=4S△ABD , 求点P的坐标.22. 小明大学毕业回家乡创业,第一期培植盆景与花卉各50盆售后统计,盆景的平均每盆利润是160元,花卉的平均每盆利润是19元,调研发现:①盆景每增加1盆,盆景的平均每盆利润减少2元;每减少1盆,盆景的平均每盆利润增加2元;②花卉的平均每盆利润始终不变.
小明计划第二期培植盆景与花卉共100盆,设培植的盆景比第一期增加x盆,第二期盆景与花卉售完后的利润分别为W1 , W2(单位:元)
(1)、用含x的代数式分别表示W1 , W2;
(2)、当x取何值时,第二期培植的盆景与花卉售完后获得的总利润W最大,最大总利润是多少?23. 如图1,BC是⊙O的直径,点A在⊙O上,AD⊥BC,垂足为D, ,BE分别交AD、AC于点F、G.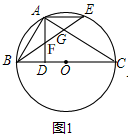
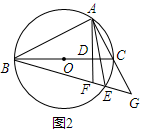 (1)、判断△FAG的形状,并说明理由;(2)、如图2,若点E和点A在BC的两侧,BE、AC的延长线交于点G,AD的延长线交BE于点F,其余条件不变,(1)中的结论还成立吗?请说明理由;(3)、在(2)的条件下,若BG=26,BD﹣DF=7,求AB的长.24. 如图,直线
(1)、判断△FAG的形状,并说明理由;(2)、如图2,若点E和点A在BC的两侧,BE、AC的延长线交于点G,AD的延长线交BE于点F,其余条件不变,(1)中的结论还成立吗?请说明理由;(3)、在(2)的条件下,若BG=26,BD﹣DF=7,求AB的长.24. 如图,直线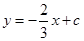 与
与 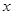 轴交于点
轴交于点 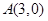 ,与
,与  轴交于点
轴交于点 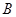 ,抛物线
,抛物线 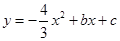 经过点
经过点 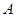 ,
, 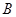 .
.  (1)、求点B的坐标和抛物线的解析式;(2)、M(m,0)为x轴上一个动点,过点M垂直于x轴的直线与直线AB和抛物线分别交于点P、N,
(1)、求点B的坐标和抛物线的解析式;(2)、M(m,0)为x轴上一个动点,过点M垂直于x轴的直线与直线AB和抛物线分别交于点P、N,①点
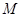 在线段
在线段 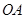 上运动,若以
上运动,若以 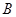 ,
, 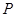 ,
, 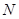 为顶点的三角形与
为顶点的三角形与 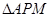 相似,求点
相似,求点 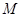 的坐标;
的坐标;②点
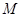 在
在 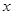 轴上自由运动,若三个点
轴上自由运动,若三个点 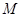 ,
, 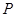 ,
, 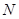 中恰有一点是其它两点所连线段的中点(三点重合除外),则称
中恰有一点是其它两点所连线段的中点(三点重合除外),则称 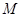 ,
, 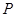 ,
, 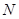 三点为“共谐点”.请直接写出使得
三点为“共谐点”.请直接写出使得 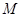 ,
, 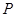 ,
, 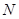 三点成为“共谐点”的
三点成为“共谐点”的 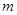 的值.
的值.