浙江省绍兴市越城区五校联考2019-2020学年八年级上学期数学期末考试卷
试卷更新日期:2020-03-27 类型:期末考试
一、单选题
-
1. 以下列各组数为边长,能组成一个三角形的是( )A、3,4,5 B、2,2,5 C、1,2,3 D、10,20,402. 若等腰三角形的两边长分别4和6,则它的周长是( )
A、14 B、15 C、16 D、14或163. 对一个假命题举反例时,应使所举反例( )A、满足命题的条件,并满足命题的结论 B、满足命题的条件,但不满足命题的结论 C、不满足命题的条件,但满足命题的结论 D、不满足命题的条件,也不满足命题的结论4. 若x>y,则下列式子错误的是( )A、x﹣3>y﹣3 B、﹣3x>﹣3y C、x+3>y+3 D、5. 点P(﹣2,﹣4)与点Q(6,﹣4)的位置关系是( )A、关于直线x=2对称 B、关于直线y=2对称 C、关于x轴对称 D、关于y轴对称6. 如图,已知AD是△ABC的BC边上的高,下列能使△ABD≌△ACD的条件是( )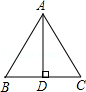 A、AB=AC B、∠BAC=90° C、BD=AC D、∠B=45°7. 如图,坐标平面上有P,Q两点,其坐标分别为(5,a),(b,7),根据图中P,Q两点的位置,则点(6-b,a-10)在( )
A、AB=AC B、∠BAC=90° C、BD=AC D、∠B=45°7. 如图,坐标平面上有P,Q两点,其坐标分别为(5,a),(b,7),根据图中P,Q两点的位置,则点(6-b,a-10)在( )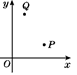 A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 已知不等式x﹣1≥0,此不等式的解集在数轴上表示为( )A、
A、第一象限 B、第二象限 C、第三象限 D、第四象限8. 已知不等式x﹣1≥0,此不等式的解集在数轴上表示为( )A、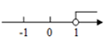 B、
B、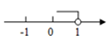 C、
C、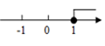 D、
D、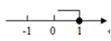 9. 如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( )
9. 如图,在Rt△ABC中,∠C=90°,AC=9,BC=12,则点C到AB的距离是( ) A、 B、 C、 D、10. 如图,直线y=x+m与y=nx﹣5n(n≠0)的交点的横坐标为3,则关于x的不等式x+m>nx﹣5n>0的整数解为( )
A、 B、 C、 D、10. 如图,直线y=x+m与y=nx﹣5n(n≠0)的交点的横坐标为3,则关于x的不等式x+m>nx﹣5n>0的整数解为( )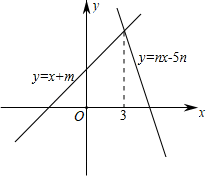 A、3 B、4 C、5 D、6
A、3 B、4 C、5 D、6二、填空题
-
11. 下列图形中全等图形是(填标号).
 12.
12.如图,身高为x cm的1号同学与身高为y cm的2号同学站在一起时,如果用一个不等式来表示他们的身高关系,则这个式子可以表示成x y(用“>”或“<”填空).
 13. 在△ABC中,已知∠A=60°,∠B=80°,则∠C的外角的度数是.14. 如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E为垂足,连接CD,若BD=1,则AC的长是.
13. 在△ABC中,已知∠A=60°,∠B=80°,则∠C的外角的度数是.14. 如图.在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于D,E为垂足,连接CD,若BD=1,则AC的长是.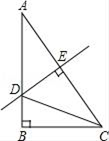 15. 甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.图中l甲、l乙分别表示甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分)变化的函数图象,则每分钟乙比甲多行驶千米.
15. 甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.图中l甲、l乙分别表示甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分)变化的函数图象,则每分钟乙比甲多行驶千米.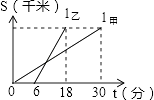
三、解答题
-
16. 如图,直线l1:y=﹣2x+2交x轴于点A,交y轴于点B,直线l2:y= x+1交x轴于点D,交y轴于点C,直线l1、l2交于点M.
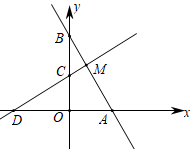 (1)、点M坐标为;(2)、若点E在y轴上,且△BME是以BM为一腰的等腰三角形,则E点坐标为.17. 解不等式组18. 如图,在方格纸中,以格点连线为边的三角形叫格点三角形,请按要求完成下列操作:先将格点△ABC向右平移4个单位得到△A1B1C1 , 再将△A1B1C1绕点C1点旋转180°得到△A2B2C2.
(1)、点M坐标为;(2)、若点E在y轴上,且△BME是以BM为一腰的等腰三角形,则E点坐标为.17. 解不等式组18. 如图,在方格纸中,以格点连线为边的三角形叫格点三角形,请按要求完成下列操作:先将格点△ABC向右平移4个单位得到△A1B1C1 , 再将△A1B1C1绕点C1点旋转180°得到△A2B2C2.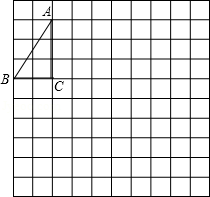 19. 在△ABC中,∠ABC=45°,F是高AD与高BE的交点.
19. 在△ABC中,∠ABC=45°,F是高AD与高BE的交点.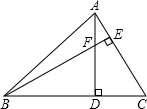 (1)、求证:△ADC≌△BDF.(2)、连接CF,若CD=4,求CF的长.20. 在平面直角坐标系中,已知直线l:y=﹣ x+2交x轴于点A,交y轴于点B,直线l上的点P(m,n)在第一象限内,设△AOP的面积是S.
(1)、求证:△ADC≌△BDF.(2)、连接CF,若CD=4,求CF的长.20. 在平面直角坐标系中,已知直线l:y=﹣ x+2交x轴于点A,交y轴于点B,直线l上的点P(m,n)在第一象限内,设△AOP的面积是S.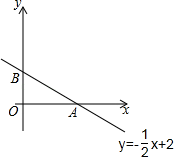 (1)、写出S与m之间的函数表达式,并写出m的取值范围.(2)、当S=3时,求点P的坐标.(3)、若直线OP平分△AOB的面积,求点P的坐标.21. 如图,已知在△ABC中,AB=AC,D是BC边上任意一点,E在AC边上,且AD=AE.
(1)、写出S与m之间的函数表达式,并写出m的取值范围.(2)、当S=3时,求点P的坐标.(3)、若直线OP平分△AOB的面积,求点P的坐标.21. 如图,已知在△ABC中,AB=AC,D是BC边上任意一点,E在AC边上,且AD=AE.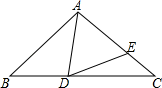 (1)、若∠BAD=40°,求∠EDC的度数;(2)、若∠EDC=15°,求∠BAD的度数;(3)、根据上述两小题的答案,试探索∠EDC与∠BAD的关系.22. 某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.(1)、求每台A型电脑和B型电脑的销售利润;(2)、该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.
(1)、若∠BAD=40°,求∠EDC的度数;(2)、若∠EDC=15°,求∠BAD的度数;(3)、根据上述两小题的答案,试探索∠EDC与∠BAD的关系.22. 某商店销售10台A型和20台B型电脑的利润为4000元,销售20台A型和10台B型电脑的利润为3500元.(1)、求每台A型电脑和B型电脑的销售利润;(2)、该商店计划一次购进两种型号的电脑共100台,其中B型电脑的进货量不超过A型电脑的2倍,设购进A型电脑x台,这100台电脑的销售总利润为y元.①求y关于x的函数关系式;
②该商店购进A型、B型电脑各多少台,才能使销售总利润最大?
(3)、实际进货时,厂家对A型电脑出厂价下调m(0<m<100)元,且限定商店最多购进A型电脑70台,若商店保持同种电脑的售价不变,请你根据以上信息及(2)中条件,设计出使这100台电脑销售总利润最大的进货方案.23. 如图①,已知直线y=﹣2x+4与x轴、y轴分别交于点A、C , 以OA、OC为边在第一象限内作长方形OABC .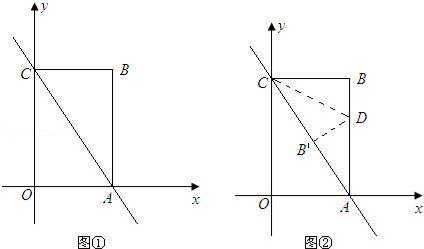 (1)、求点A、C的坐标;(2)、将△ABC对折,使得点A的与点C重合,折痕交AB于点D , 求直线CD的解析式(图②);(3)、在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.
(1)、求点A、C的坐标;(2)、将△ABC对折,使得点A的与点C重合,折痕交AB于点D , 求直线CD的解析式(图②);(3)、在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请求出所有符合条件的点P的坐标;若不存在,请说明理由.